第二章例题与课后作业
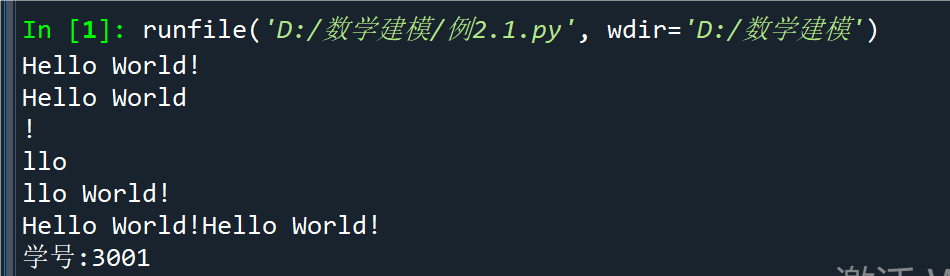
例2.1字符串操作示例
点击查看代码
str1 = "Hello World!"
print(str1)
print(str1[0:-1])
print(str1[-1])
print(str1[2:5])
print(str1[2:])
print(str1 * 2)
print("学号:3001")
例2.2统计下列5行字符串中字符a,c,g,t出现的的频数
点击查看代码
import numpy as np
a = []
with open("D:\数学建模\例2.2.txt") as f:
for (i, s) in enumerate(f):
a.append([s.count('a'), s.count('c'),
s.count('g'),s.count('t')])
b = np.array(a); print(b)
print("学号:3001")

例2.3列表操作示例
点击查看代码
L = ['abc', 12, 3.45, 'Python', 2.789]
print(L)
print(L[0])
L[0] = 'a'
L[1:3] = ['b', 'Hello']
print(L)
L[2:4] = []
print(L)
print("学号:3001")

例2.4使用列表推导式实现嵌套列表的平铺
点击查看代码
a = [[1,2,3],[4,5,6],[7,8,9]]
d = [c for b in a for c in b]
print(d)
print("学号:3001")

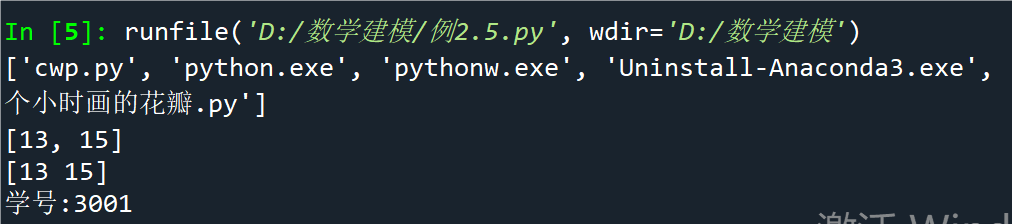
例2.5在列表推导式中使用if过滤不符合条件的元素
点击查看代码
import os
fn = [filename for filename in
os.listdir('D:\PythonWork')
if filename.endswith(('.exe','.py'))]
print(fn)
print("学号:3001")
from numpy.random import randint
import numpy as np
a = randint(10,20,16)
ma = max(a)
ind1 = [index for index,value in enumerate(a) if value == ma]
ind2 = np.where(a == ma)
print(ind1);print(ind2[0])
print("学号:3001")
例2.6元组操作示例
点击查看代码
T = ('abc', 12, 3.45, 'Python', 2.789)
print(T)
print(T[-1])
print(T[1:3])
print("学号:3001")

例2.7集合操作示例
点击查看代码
student = {'Tom', 'Jim', 'Mary', 'Tom', 'Jack', 'Rose'}
print(student)
a = set('abcdabc')
print(a)
print("学号:3001")

例2.8字典操作示例
点击查看代码
dict1 ={'Alice': '123', 'Beth': '456', 'Cecil': 'abc'}
print(dict1['Alice'])
dict1['new'] = 'Hello'
dict1['Alice'] = '1234'
dict2 = {'abc': 123, 456: 78.9}
print(dict2[456])
print("学号:3001")

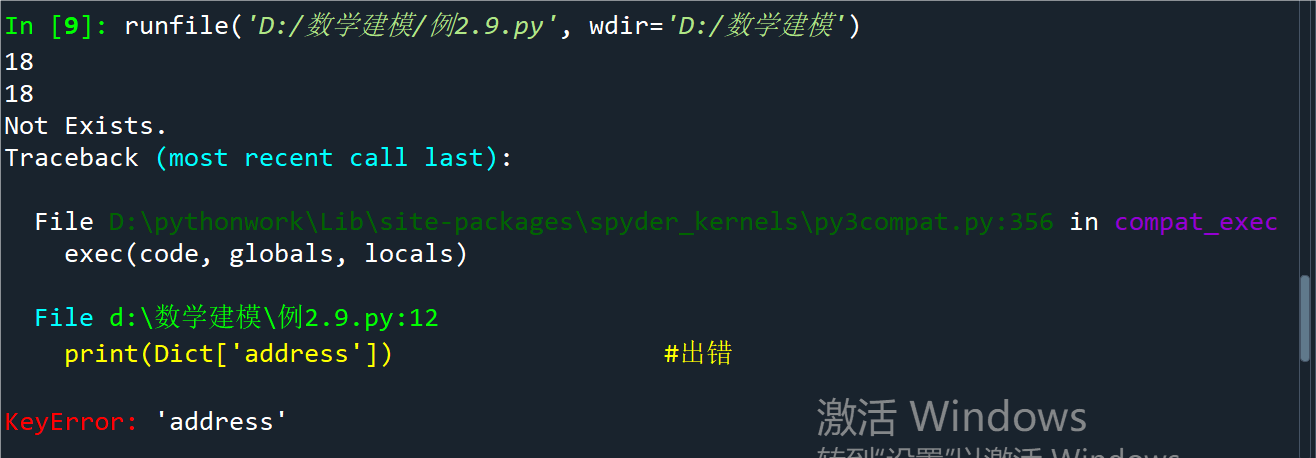
例2.9字典的get()方法使用示例
点击查看代码
Dict={'age':18,'score':[98,97],'name':'Zhang','sex':'male'}
print(Dict['age']) #输出18
print(Dict.get('age')) #输出18
print(Dict.get('address','Not Exists.'))#输出 No Exists.
print(Dict['address']) #出错
print("学号:3001")
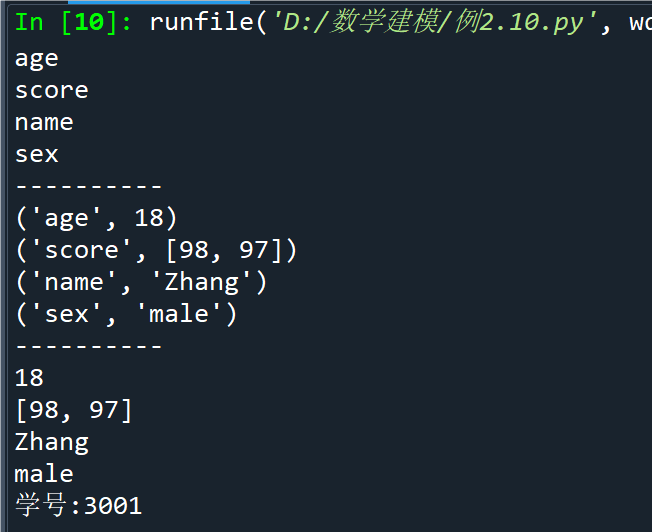
例2.10字典元素的访问示例
点击查看代码
Dict={'age':18,'score':[98,97],'name':'Zhang','sex':'male'}
for item in Dict:
print(item)
print("----------")
for item in Dict.items():
print(item)
print("----------")
for value in Dict.values():
print(value)
print("学号:3001")
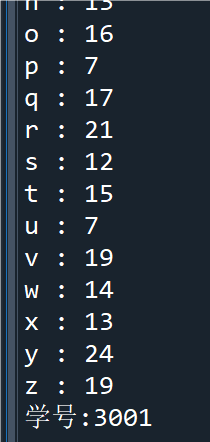
例2.11首先生成包含1000个随机字符的字符串,然后统计每个字符的出现次数,注意get()方法的应用
2.11的(1)
点击查看代码
import string
import random
x=string.ascii_letters+string.digits
y=''.join([random.choice(x) for i in range(1000)])
#choice()用于从多个元素中随机选择一个
d=dict() #构造空字典
for ch in y:
d[ch]=d.get(ch,0)+1;
for k,v in sorted(d.items()):
print(k,':',v)
print("学号:3001")
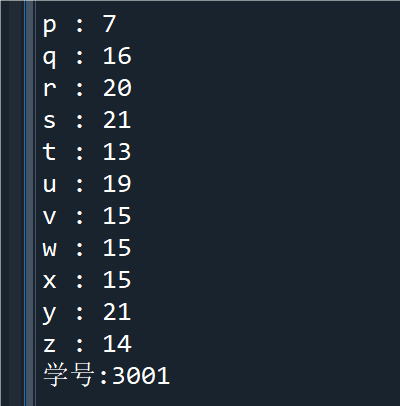
2.11的(2)
点击查看代码
import string, random, collections #依次加载三个模块
x=string.ascii_letters+string.digits
y=''.join([random.choice(x) for i in range(1000)])
count=collections.Counter(y)
for k,v in sorted(count.items()):
print(k, ':', v)
print("学号:3001")
例2.12分别编写求n!和输出斐波那契数列的函数,并调用两个函数进行测试
点击查看代码
def factorial(n):
r = 1
while n > 1:
r *= n
n -= 1
return r
def fib(n):
a, b = 1, 1
while a < n:
print(a, end=' ')
a, b = b, a+b
print('%d! = %d'%(5,factorial(5)))
fib(200)
print("学号:3001")

例2.13数据分组
点击查看代码
def bifurcate_by(L, fn):
return [[x for x in L if fn(x)],
[x for x in L if not fn(x)]]
s=bifurcate_by(['beep', 'boop', 'foo', 'bar'], lambda x: x[0] =='b')
print(s)
print("学号:3001")

例2.14用匿名函数,求3个数的乘积和列表元素的值
点击查看代码
f=lambda x, y, z: x * y * z
L=lambda x: [x**2, x**3, x**4]
print(f(3,4,5)); print(L(2))
print("学号:3001")

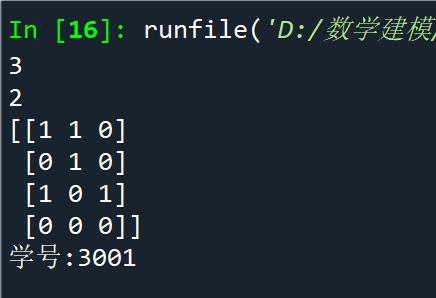
例2.15加载模块示例
点击查看代码
import math
import random
import numpy.random as nr
a=math.gcd(12,21)
b=random.randint(0,2)
c=nr.randint(0,2,(4,3))
print(a); print(b); print(c)
print("学号:3001")
例2.16导入模块示例
点击查看代码
from random import sample
from numpy.random import randint
a=sample(range(10),5)
b=randint(0,10,15)
print(a); print(b)
print("学号:3001")

例2.17导入模块示例
点击查看代码
from math import *
a=sin(3)
b=pi
c=e
d=radians(180)
print(a);print(b);print(c);print(d)
print("学号:3001")

例2.18调入自定义函数factorial()和fin(),计算6!,输出300以内的斐波那契数列
点击查看代码
def factorial(n):
r = 1
while n > 1:
r *= n
n -= 1
return r
def fib(n):
a,b = 1,1
while a < n:
print(a,end=' ')
a,b = b,a+b
print('%d! = %d'%(6,factorial(6)))
fib(300)
print("学号:3001")

例2.19sorted()使用示例
点击查看代码
import numpy.random as nr
x1 = list(range(9, 21))
nr.shuffle(x1) # shuffle()用来随机打乱顺序
x2 = sorted(x1) # 按照从小到大排序
x3 = sorted(x1, reverse = True) # 按照从大到小排序
x4 = sorted(x1, key = lambda item: len(str(item))) # 以指定的规则排序
print(x1); print(x2); print(x3); print(x4)
print("学号:3001")

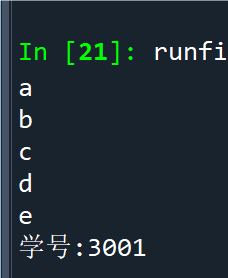
例2.20enumerate()函数使用示例
点击查看代码
x1 = 'abcde'
x2 = list(enumerate(x1))
for ind, ch in enumerate(x1):
print(ch)
print("学号:3001")
例2.21map()函数使用示例
点击查看代码
import random
x = random.randint(1e5, 1e8) # 生成一个随机整数
y = list(map(int, str(x))) # 提出每位上的数字
z = list(map(lambda x, y: x%2 == 1 and y%2 == 0, [1, 3, 2, 4, 1], [3, 2, 1, 2]))
print(x); print(y); print(z)
print("学号:3001")

例2.22filter()函数使用示例
点击查看代码
a = filter(lambda x: x>0, [1, 11, 2, 45, 7, 6, 13])
b = filter(lambda x: x.isalnum(), ['abc', 'xy12', '***'])
# isalnum() 是测试是否为字母或数字的方法
print(list(a)); print(list(b))
print("学号:3001")

例2.23过滤重复值
点击查看代码
def filter_non_unique(L):
return [item for item in L if L.count(item) == 1]
a = filter_non_unique([1, 2, 2, 3, 4, 4, 5])
print(a)
print("学号:3001")
例2.24zip()函数使用示例
点击查看代码
s1 = [str(x)+str(y) for x, y in zip(['v']*4, range(1, 5))]
s2 = list(zip('abcd', range(4)))
print(s1); print(s2)
print("学号:3001")

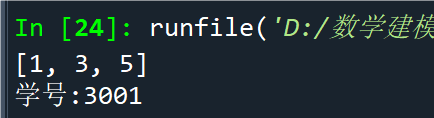
例2.25数组生成示例1
点击查看代码
import numpy as np
a1 = np.array([1, 2, 3, 4]) # 生成整型数组
a2 = a1.astype(float)
a3 = np.array([1, 2, 3, 4], dtype = float) # 浮点数
print(a1.dtype); print(a2.dtype); print(a3.dtype)
b = np.array([[1, 2, 3], [4, 5, 6]])
c = np.arange(1, 4) # 生成数组 [1, 2, 3, 4]
d = np.linspace(1, 4, 4) # 生成数组 [1, 2, 3, 4]
e = np.logspace(1, 3, 3, base = 2) # 生成数组 [2, 4, 8]
print(b);print(c);print(d);print(e)
print("学号:3001")
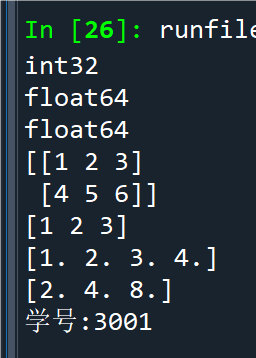
例2.26数组生成示例2
点击查看代码
import numpy as np
a = np.ones(4, dtype = int) # 输出[1, 1, 1, 1]
b = np.ones((4,), dtype = int) # 同a
c = np.ones((4, 1)) # 输出 4 行 1 列的数组
d = np.zeros(4) # 输出 [0, 0, 0, 0]
e = np.empty(3) # 生成 3 个元素的空数组行向量
f = np.eye(3) # 生成 3 阶单位矩阵
g = np.eye(3, k = 1) # 生成第 k 对角线元素为 1,其它元素为 0 的 3 阶方针
h = np.zeros_like(a) # 生成与 a 同维的全 0 数组
print(a);print(b);print(c);print(d)
print(e);print(f);print(g);print(h)
print("学号:3001")
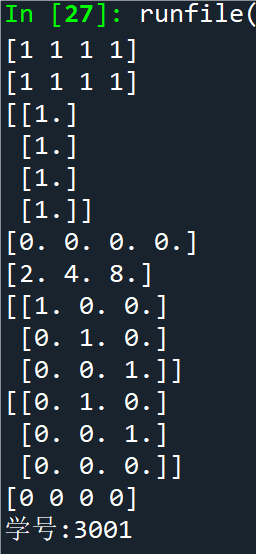
例2.27数组元素的索引示例
点击查看代码
import numpy as np
a = np.arange(16).reshape(4,4) # 生成 4 行 4 列的数组
b = a[1][2] # 输出6
c = a[1, 2] # 同 b
d = a[1:2, 2:3] # 输出[[6]]
x = np.array([0, 1, 2, 1])
print(a[x==1]) # 输出 a 的第 2、4 行元素
print("学号:3001")

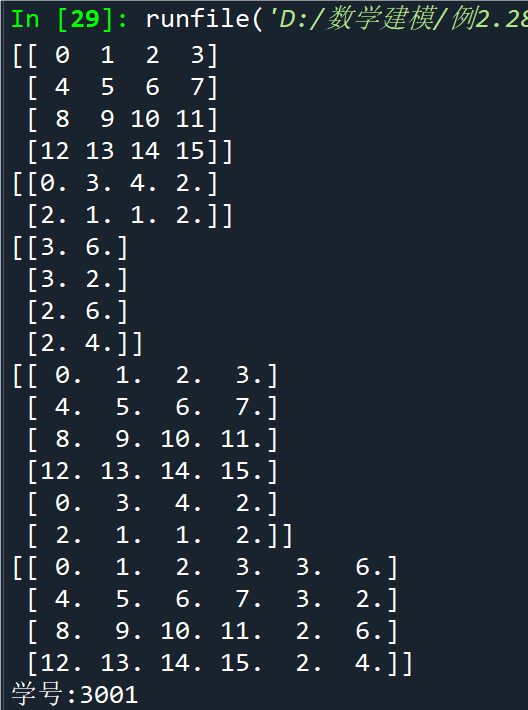
例2.28矩阵合并示例
点击查看代码
import numpy as np
a = np.arange(16).reshape(4, 4) # 生成 4 行 4 列的数组
b = np.floor(5*np.random.random((2, 4)))
c = np.ceil(6*np.random.random((4, 2)))
d = np.vstack([a, b]) # 上下合并矩阵
e = np.hstack([a, c]) # 左右合并矩阵
print(a);print(b);print(c);print(d);print(e)
print("学号:3001")
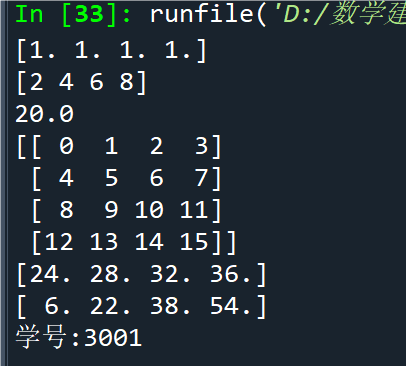
例2.29矩阵分割示例
点击查看代码
import numpy as np
a = np.arange(16).reshape(4, 4) # 生成 4 行 4 列的数组
b = np.vsplit(a, 2) # 行分割
print('行分割:\n', b[0], '\n', b[1])
c = np.hsplit(a, 4) # 列分割
print('列分割:\n', c[0], '\n', c[1], '\n', c[2], '\n', c[3])
print("学号:3001")
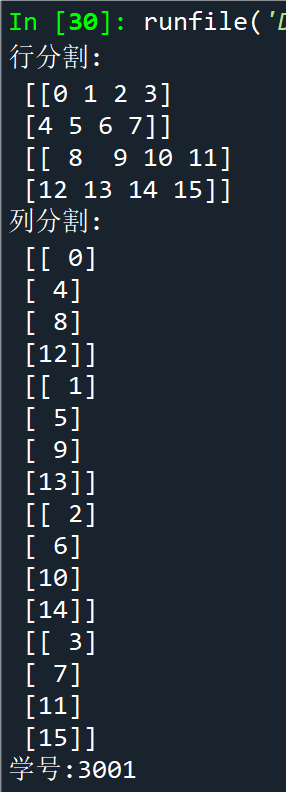
例2.30矩阵元素求和示例
点击查看代码
import numpy as np
a = np.array([[0, 3, 4], [1, 6, 4]])
b = a.sum() # 使用方法,求矩阵所有元素的和
c1 = sum(a) # 内置函数求矩阵逐列元素的和
c2 = np.sum(a, axis=0) # 使用函数,求矩阵逐列元素的和
c3 = np.sum(a, axis=0, keepdims=True) # 逐列求和
print(c2.shape, c3.shape) # c2是(3,)数组,c3是(1, 3)数组
print("学号:3001")
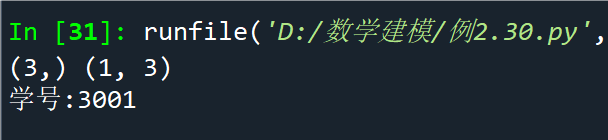
例2.31逐个元素运算示例
点击查看代码
import numpy as np
a = np.array([[0, 3, 4], [1, 6, 4]])
b = np.array(([1, 2, 3], [2, 1, 4]))
c = a/b # 两个矩阵对应元素相除
d = np.array([2, 3, 2])
e = a*b # d 先广播成与 a 同维数的矩阵,再逐个元素相乘
f = np.array([[3], [2]])
g = a*f # f 先广播成与 a 同维数的矩阵,再逐个元素相乘
h = a**(1/2) # a 矩阵逐个元素的 1/2 次幂
print(a);print(b);print(c);print(d)
print(e);print(f);print(g);print(h)
print("学号:3001")
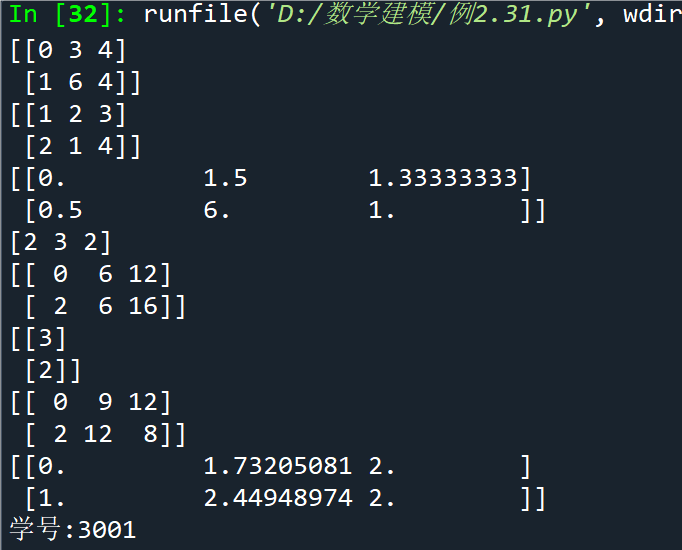
例2.32矩阵乘法示例
点击查看代码
import numpy as np
a = np.ones(4)
b = np.arange(2, 10, 2)
c = a @ b # a 作为行向量,b 作为列向量
d = np.arange(16).reshape(4, 4)
f = a @ d # a 作为行向量
g = d @ a # a 作为列向量
print(a);print(b);print(c)
print(d);print(f);print(g)
print("学号:3001")
例2.33求下列矩阵的各个行向量的2范数,各个列向量的2范数和矩阵2范数
点击查看代码
import numpy as np
a = np.array([[0, 3, 4], [1, 6, 4]])
b = np.linalg.norm(a, axis = 1) # 求行向量 2 范数
c = np.linalg.norm(a, axis = 0) # 求列向量 2 范数
d = np.linalg.norm(a) # 求矩阵 2 范数
print('行向量 2 范数为:', np.round(b, 4))
print('列向量 2 范数为:', np.round(c, 4))
print('矩阵 2 范数为:', np.round(d, 4))
print("学号:3001")

例2.34求解线性方程组
点击查看代码
import numpy as np
a = np.array([[3, 1],[1, 2]])
b = np.array([9, 8])
x1 = np.linalg.inv(a) @ b # 第一种解法
x2 = np.linalg.solve(a, b) # 第二种解法
print(x1); print(x2)
print("学号:3001")
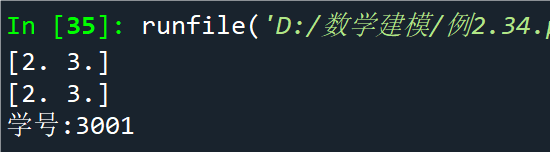
例2.35求解线性方程组
点击查看代码
import numpy as np
a = np.array([[3, 1], [1, 2], [1, 1]])
b = np.array([9, 8, 6])
x = np.linalg.pinv(a) @ b
print(np.round(x, 4))
print("学号:3001")
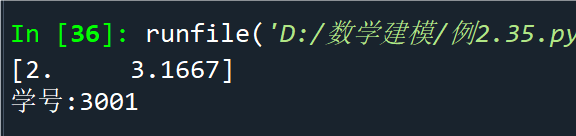
例2.36求下列矩阵的特征值和特征向量
点击查看代码
import numpy as np
a = np.eye(4)
b = np.rot90(a)
c, d = np.linalg.eig(b)
print('特征值为:', c)
print('特征向量为:\n', d)
print("学号:3001")
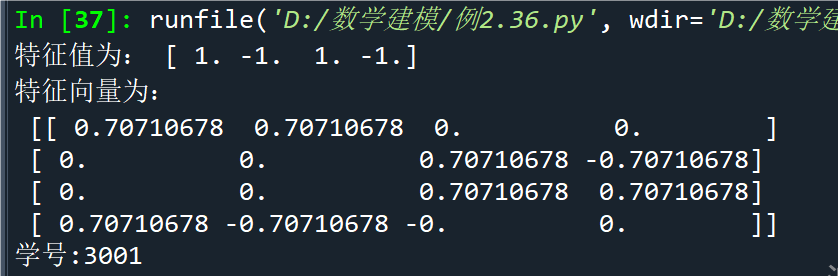
例2.37生成服从标准正态分布的24*4随机数矩阵,并保持为DataFrame数据结构
点击查看代码
import pandas as pd
import numpy as np
dates = pd.date_range(start = '20191101', end = '20191124', freq = 'D')
a1 = pd.DataFrame(np.random.randn(24, 4), index = dates, columns = list('ABCD'))
a2 = pd.DataFrame(np.random.rand(24, 4))
print(a1);print(a2)
print("学号:3001")
例2.38数据写入文件示例
点击查看代码
import pandas as pd
import numpy as np
# 生成日期索引和随机数据
dates = pd.date_range(start='20191101', end='20191124', freq='D')
a1 = pd.DataFrame(np.random.randn(24, 4), index=dates, columns=list('ABCD'))
a2 = pd.DataFrame(np.random.randn(24, 4))
# 将DataFrame保存到Excel和CSV文件
a1.to_excel('data2_38_1.xlsx')
a2.to_csv('data2_38_2.csv')
# 使用with语句自动管理ExcelWriter对象的生命周期
with pd.ExcelWriter('data2_38_3.xlsx') as f:
a1.to_excel(f, "Sheet1")
a2.to_excel(f, "Sheet2")
print("学号:3001")

例2.39从文件中读入数据示例
点击查看代码
import pandas as pd
a = pd.read_csv('data2_38_2.csv', usecols = range(1, 5))
b = pd.read_excel('data2_38_3.xlsx', "Sheet2", usecols = range(1, 5))
print(a); print(b)
print("学号:3001")
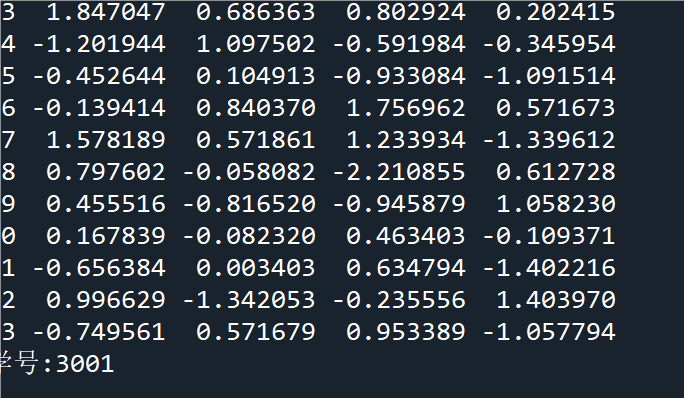
例2.40DataFrame数据的拆分、合并和分组计算示例
点击查看代码
import pandas as pd
import numpy as np
d = pd.DataFrame(np.random.randint(1, 6, (10, 4)), columns = list('ABCD'))
d1 = d[:4] # 获取前 4 行数据
d2 = d[4:] # 获取第 5 行以后的数据
dd = pd.concat([d1, d2]) # 数据行合并
s1 = d.groupby('A').mean() # 数据分组求均值
s2 = d.groupby('A').apply(sum) # 数据分组求和
print(d1);print(d2)
print("学号:3001")
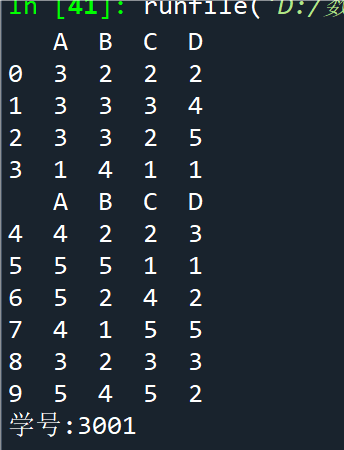
例2.41DataFrame数据操作示例
点击查看代码
import pandas as pd
import numpy as np
a = pd.DataFrame(np.random.randint(1, 6, (5, 3)),
index = ['a', 'b', 'c', 'd', 'e'],
columns = ['one', 'two', 'three'])
a.loc['a', 'one'] = np.nan # 修改第 1 行第 1 列的数据
b = a.iloc[1:3, 0:2].values # 提取第 2、3 行,第 1、2 列数据
a['four'] = 'bar' # 增加第 4 列数据
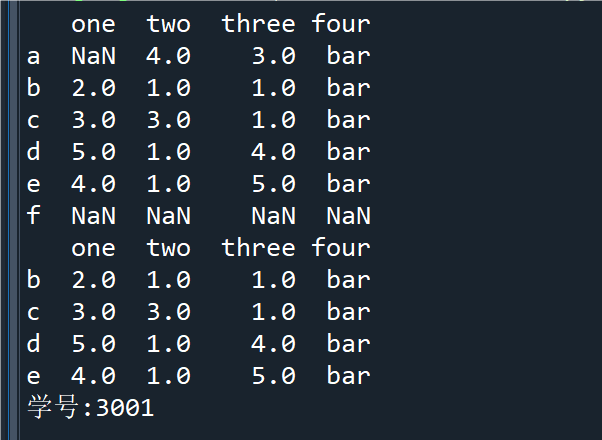
a2 = a.reindex(['a', 'b', 'c', 'd', 'e', 'f'])
a3 = a2.dropna() # 删除有不确定值的行
print(a2);print(a3)
print("学号:3001")
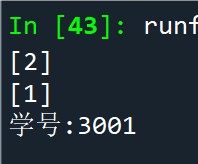
例2.42遍历文件data2_2.txt中所有行,统计每一行中字符的个数
点击查看代码
with open('data2_2.txt',encoding='utf-8') as fp:
L1=[]; L2=[];
for line in fp:
L1.append(len(line))
L2.append(len(line.strip())) # 去掉换行符
data = [str(num)+'\t' for num in L2] # 转换为字符串
print(L1); print(L2)
with open('data2_2.txt', 'w') as fp2:
fp2.writelines(data)
print("学号:3001")
例2.43随机产生一个数据矩阵,把它存入具有不同分隔符格式的文本文件中,再把数据从文本文件中提取出来
点击查看代码
import numpy as np
a = np.random.rand(6, 8) # 生成 6*8 的[0, 1)上均匀分布的随机数矩阵
np.savetxt("data2_43_1.txt", a) # 存在以制表符分隔的文本文件
np.savetxt("data2_43_2.csv", a, delimiter=',') # 存成以逗号分隔的 CSV 文件
b = np.loadtxt("data2_43_1.txt") # 加载空格分隔的文本文件
c = np.loadtxt("data2_43_2.csv", delimiter=',') # 加载 CSV 文件
print("学号:3001")
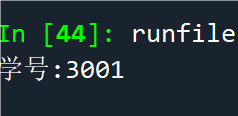
例2.44求方程在给定初值1.5附近的一个实根
点击查看代码
from scipy.optimize import fsolve, root
fx = lambda x: x**980-5.01*x**979+7.398*x**978\
-3.388*x**977-x**3+5.01*x**2-7.398*x+3.388
x1 = fsolve(fx, 1.5, maxfev=4000) #函数调用4000次
x2 = root(fx, 1.5)
print(x1,'\n','-------------'); print(x2)
print("学号:3001")
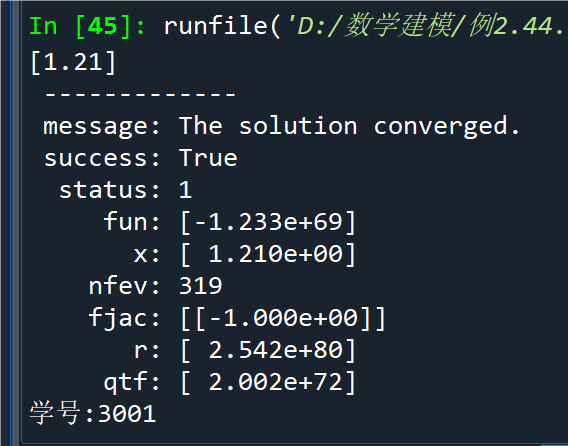
例2.45求下列方程组的一组数值解
点击查看代码
from scipy.optimize import fsolve, root
fx = lambda x: [x[0]**2+x[1]**2-1, x[0]-x[1]]
s1 = fsolve(fx, [1, 1])
s2 = root(fx, [1, 1])
print(s1,'\n','--------------'); print(s2)
print("学号:3001")
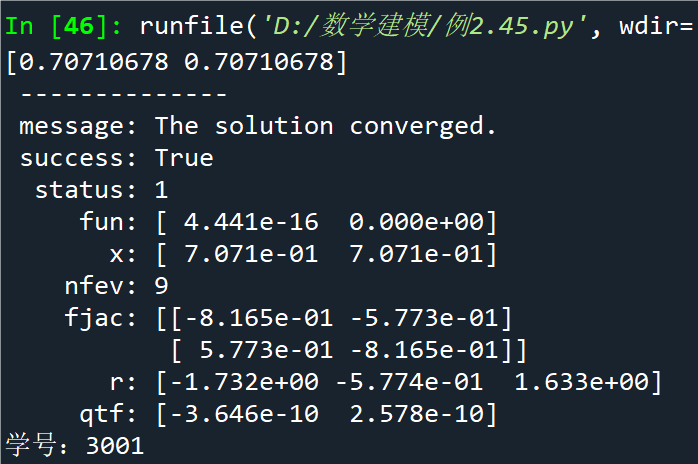
例2.46分别计算a=2,b=1; a=2,b=10时,I(a,b)的值
点击查看代码
from scipy.integrate import quad
def fun42(x, a, b):
return a*x**2+b*x
I1 = quad(fun42, 0, 1, args=(2, 1))
I2 = quad(fun42, 0, 1, args=(2, 10))
print(I1); print(I2)
print("学号:3001")
例2.47已知4个观测站的位置坐标(xi,yi)(i=1,2,3,4),每个观测站探测到距未知信号的距离di(i=1,2,3,4),已知数据见表2.9,试定位未知信号的位置坐标(x,y)
点击查看代码
from scipy.optimize import least_squares
import numpy as np
a=np.loadtxt('data2_47.txt')
x0=a[0]; y0=a[1]; d=a[2]
fx=lambda x: np.sqrt((x0-x[0])**2+(y0-x[1])**2)-d
s=least_squares(fx, np.random.rand(2))
print(s, '\n', '------------', '\n', s.x)
print("学号:3001")
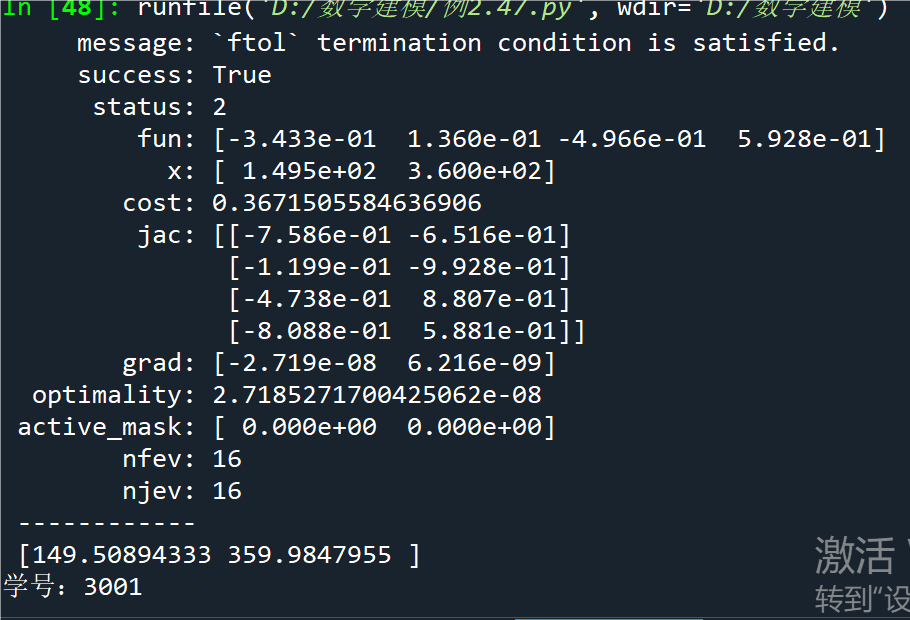
例2.48求下列矩阵的最大模特征值和对应的特征向量
点击查看代码
from scipy.sparse.linalg import eigs
import numpy as np
a = np.array([[1, 2, 3], [2, 1, 3], [3, 3, 6]], dtype=float) #必须加float,否则出错
b, c = np.linalg.eig(a)
d, e = eigs(a, 1)
print('最大模特征值为:', d)
print('对应的特征向量为:\n', e)
print("学号:3001")
例2.49利用solve求下列符号代数方程的解ax**2+bx+c=0,其中x为未知数
点击查看代码
import sympy as sp
a, b, c, x=sp.symbols('a,b,c,x')
x0=sp.solve(a*x**2+b*x+c, x)
print(x0)
print("学号:3001")

例2.50求方程组的符号解
点击查看代码
#1
import sympy as sp
sp.var('x1,x2')
s=sp.solve([x1**2+x2**2-1,x1-x2],[x1,x2])
print(s)
print("学号:3001")
#2
import sympy as sp
x = sp.var('x:2') #定义符号数组
s = sp.solve([x[0]**2+x[1]**2-1,x[0]-x[1]], x)
print(s)
print("学号:3001")

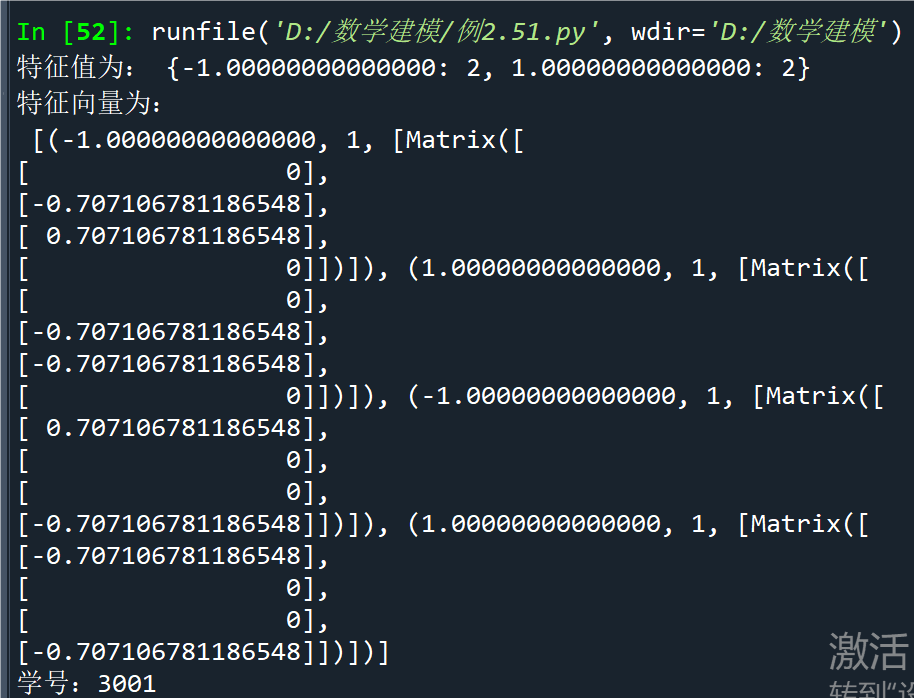
例2.51求下列矩阵的特征值和特征向量的符号解
点击查看代码
import numpy as np
import sympy as sp
a = np.identity(4) #单位矩阵的另一种写法
b = np.rot90(a)
c = sp.Matrix(b)
print('特征值为:', c.eigenvals())
print('特征向量为:\n', c.eigenvects())
print("学号:3001")
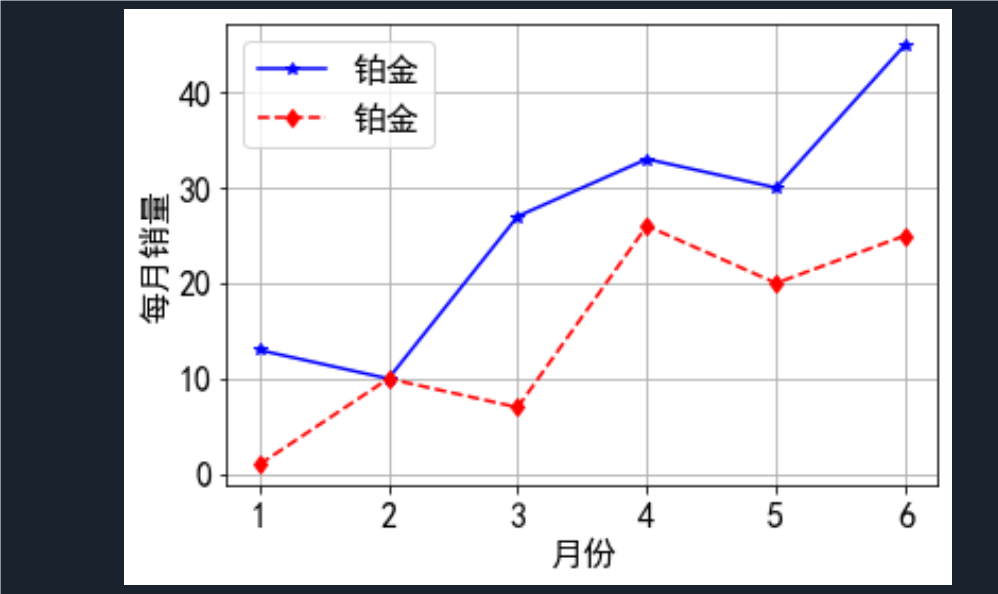
例2.52已知店铺商品的销售量如表,画出商品销售趋势图
点击查看代码
import pandas as pd
import pylab as plt
plt.rc('font',family='SimHei') #用来正常显示中文标签
plt.rc('font',size=16) #设置显示字体大小
a=pd.read_excel("data2_52.xlsx", header=None)
b=a.values #提取其中的数据
x=b[0]; y=b[1:]
plt.plot(x,y[0],'-*b',label='铂金')
plt.plot(x,y[1],'--dr',label='铂金')
plt.xlabel('月份'); plt.ylabel('每月销量')
plt.legend(loc='upper left'); plt.grid(); plt.show()
print("学号:3001")
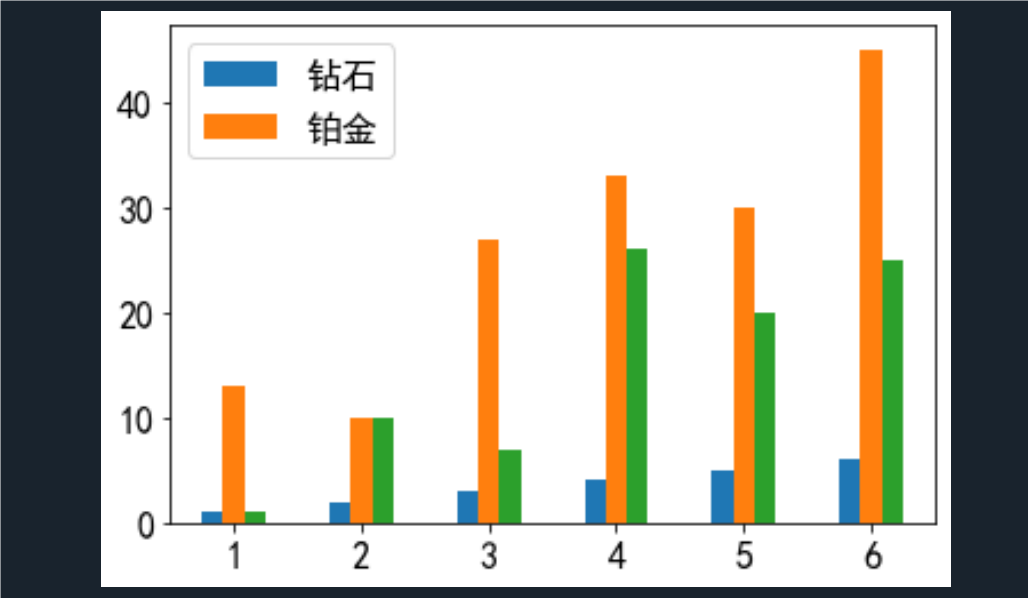
例2.53画出上表销售数据的柱状图
点击查看代码
import pandas as pd
import pylab as plt
plt.rc('font',family='SimHei') #用来正常显示中文标签
plt.rc('font',size=16) #设置显示字体大小
a=pd.read_excel("data2_52.xlsx",header=None)
b=a.T; b.plot(kind='bar'); plt.legend(['钻石', '铂金'])
plt.xticks(range(6), b[0], rotation=0); plt.show()
print("学号:3001")
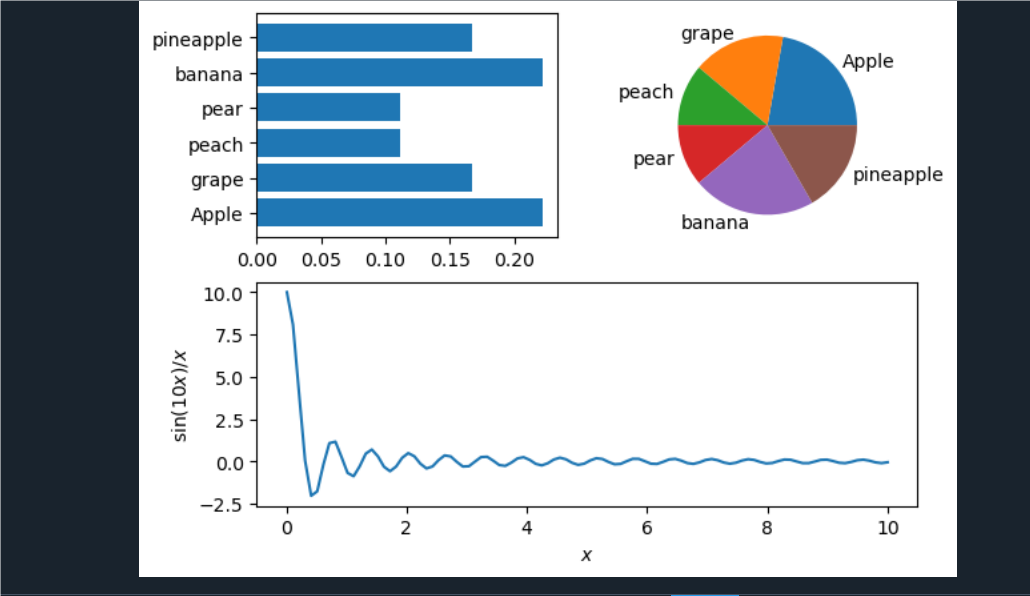
例2.54把一个窗口分成3个子窗口,分别绘制如下3个子图:
一个柱状图 一个饼图 曲线y=sin(10x)/x
点击查看代码
import pylab as plt
import numpy as np
plt.style.use('default')
y1 = np.random.randint(2, 5, 6)
y1 = y1 / sum(y1)
plt.subplot(2, 2, 1)
str = ['Apple', 'grape', 'peach', 'pear', 'banana', 'pineapple']
plt.barh(str, y1)
plt.subplot(222)
plt.pie(y1, labels=str)
plt.subplot(212)
x2 = np.linspace(0.01, 10, 100)
y2 = np.sin(10*x2) / x2
plt.plot(x2, y2)
plt.xlabel('$x$')
plt.ylabel('$\\mathrm{sin}(10x)/x$')
plt.show()
print("学号:3001")
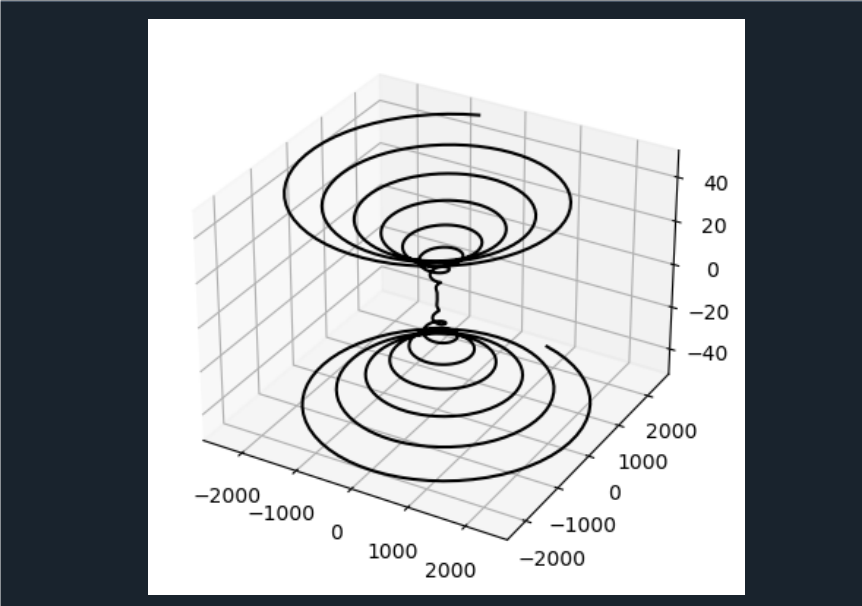
例2.55画出三维曲线x=s2sins,y=s2coss,z=s(s<-50,50>)的图形
点击查看代码
import pylab as plt
import numpy as np
ax=plt.axes(projection='3d') #设置三维图形模式
z=np.linspace(-50, 50, 1000)
x=z**2*np.sin(z); y=z**2*np.cos(z)
plt.plot(x, y, z, 'k'); plt.show()
print("学号:3001")
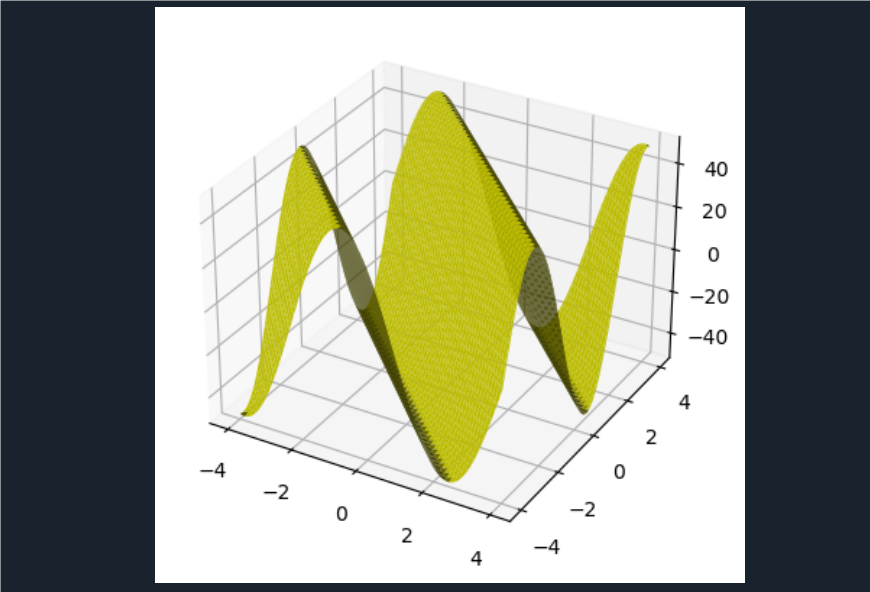
例2.56画出三维表面图z=50sin(x+y)
点击查看代码
import pylab as plt
import numpy as np
x=np.linspace(-4,4,100);
x,y=np.meshgrid(x,x)
z=50*np.sin(x+y);
ax=plt.axes(projection='3d')
ax.plot_surface(x, y, z, color='y')
plt.show()
print("学号:3001")
例2.57画出三维表面图z=sin(sqrt(x2+y2))
点击查看代码
import pylab as plt
import numpy as np
ax=plt.axes(projection='3d')
X = np.arange(-6, 6, 0.25)
Y = np.arange(-6, 6, 0.25)
X, Y = np.meshgrid(X, Y)
Z = np.sin(np.sqrt(X**2 + Y**2))
surf = ax.plot_surface(X, Y, Z, cmap='coolwarm')
plt.colorbar(surf); plt.show()
print("学号:3001")
第二章习题
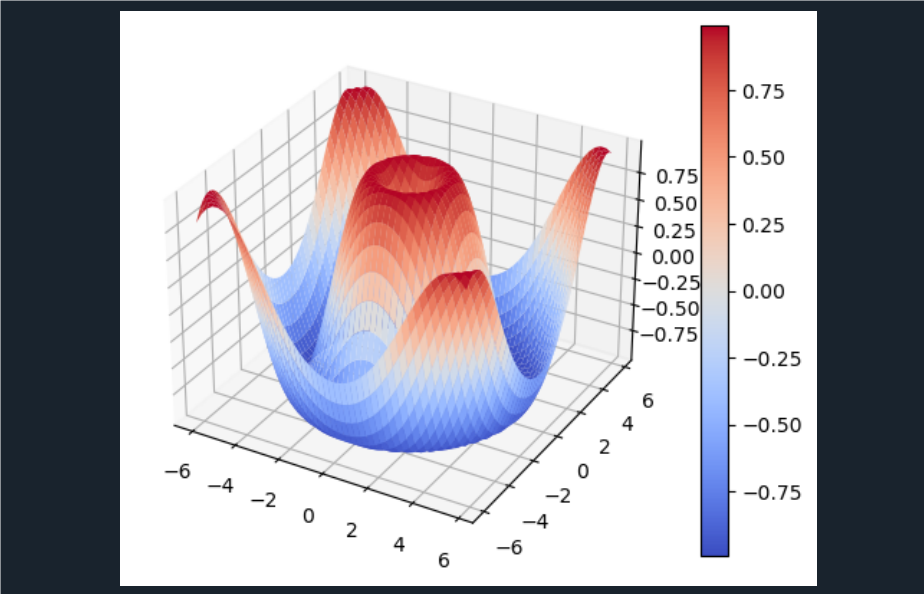
习题2.1
点击查看代码
from cProfile import label
from re import X
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import font_manager
my_font = font_manager.FontProperties(fname=
"C:/Windows/Fonts/msyh.ttc")
plt.figure(figsize=(6,5))#显示画布设置
plt.subplot(111)#第一个参数表示:行,第二个参数表示;列,第三个参数;当前图例中的激活位置
plt.xlabel(u'X数值',fontproperties=my_font)#x标签设置
plt.ylabel(u'Y数值',fontproperties=my_font)#y标签设置
plt.title(u"函数图像",fontproperties=my_font,fontsize=16)#图像名称设置
x1=np.linspace(-10,10,100)#-10,10均分100份
e= 2.718281828459
#绘制chx双曲余弦
y1=((e**x1)+(e**-x1))/2
plt.plot(x1,y1,label=u'chx')
#绘制双曲正弦shx
y2=((e**x1)-(e**-x1))/2
plt.plot(x1,y2,label=u'shx')
#绘制,1/2e^x
y3=1/2*(e**x1)
plt.plot(x1,y3,label=u'1/2e^x')
plt.legend(prop=my_font)#显示函数文本标注。
plt.show()
print("学号:3001")
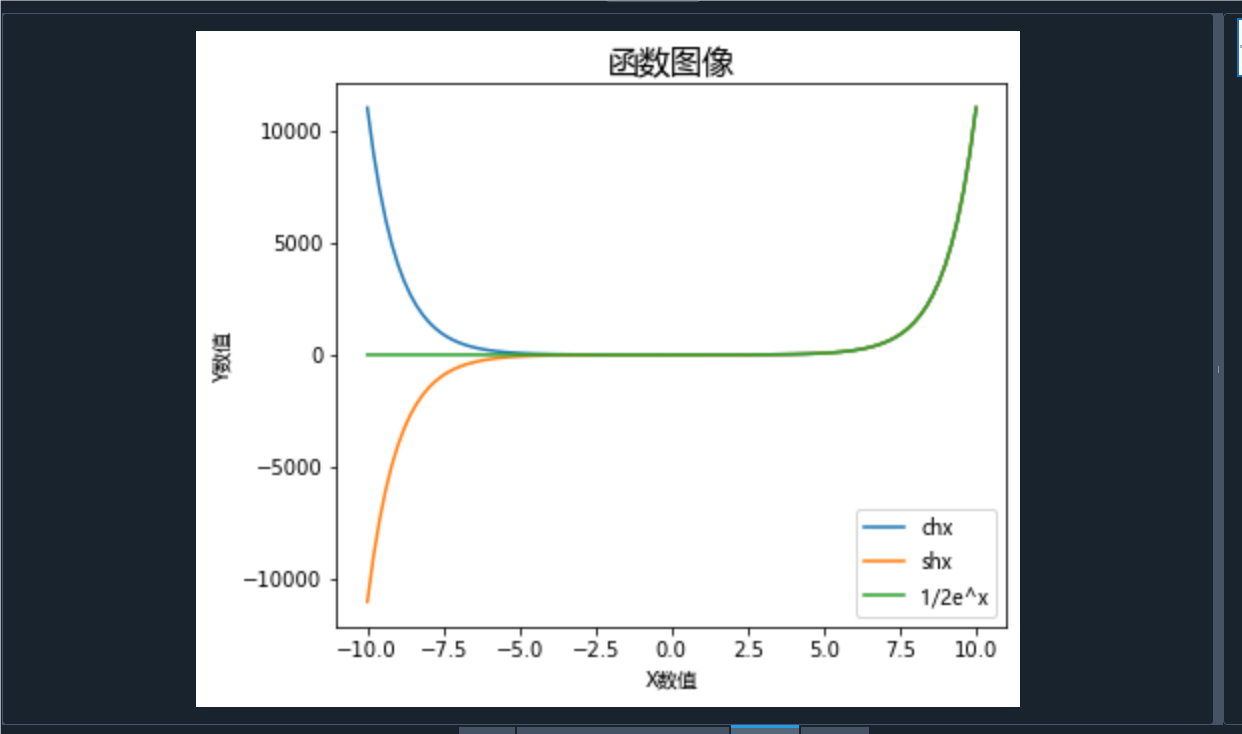
习题2.2
点击查看代码
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
def fun(t, x):
return np.exp(-t) * (t ** (x - 1))
x = np.linspace(0, 10, 100) # x 的范围
y = [quad(fun, 0, np.inf, args=i)[0] for i in x] # 计算积分
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('$ y = \int_0^{\infty} e^{-t} \cdot t^{x-1} dt $')
plt.grid(True)
plt.show()
print("学号:3001")
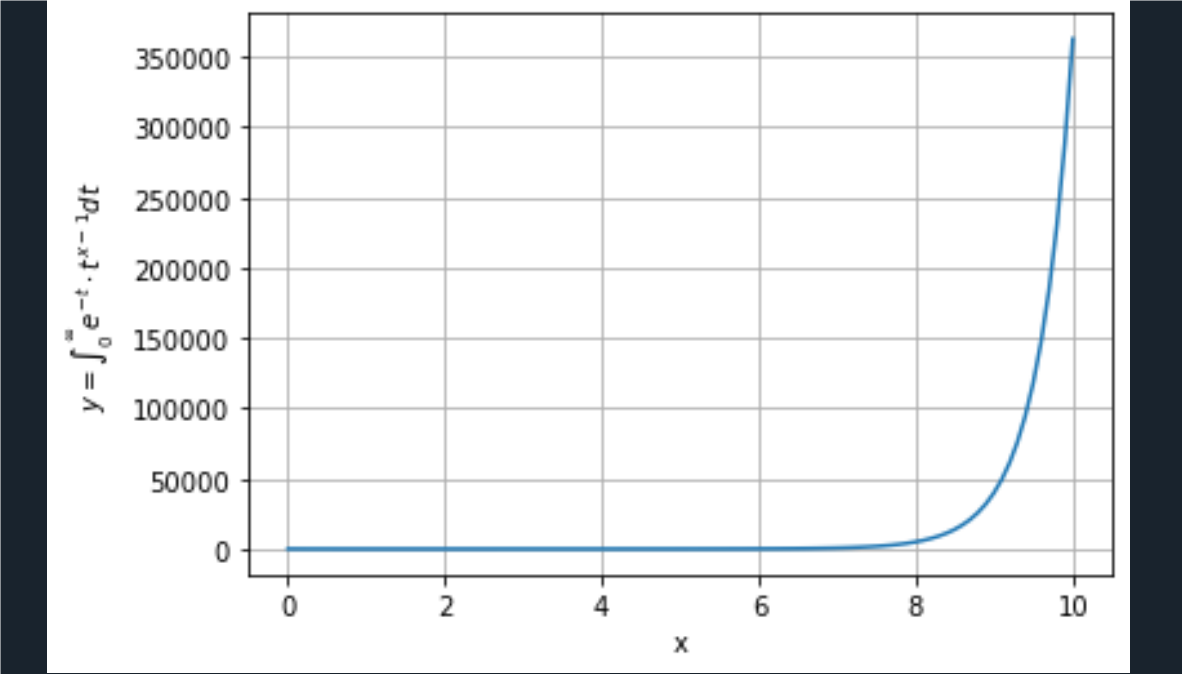
习题2.3
点击查看代码
import numpy as np
import matplotlib.pyplot as plt
k_values = [1, 2, 3, 4, 5, 6] # k的取值
x = np.linspace(-10, 10, 100) # x的范围
for k in k_values:
y = k * x ** 2 + 2 * k # 计算y值
label = f'k={k}' # 设置标注
plt.plot(x, y, label=label) # 绘制曲线
plt.xlabel('x') # 添加x轴标签
plt.ylabel('y') # 添加y轴标签
plt.legend() # 添加图例
plt.grid(True) # 添加网格线
plt.show() # 显示图形
print("学号:3001")
习题2.4
点击查看代码
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='SimHei') # 用来正常显示中文标签
plt.rc('axes', unicode_minus=False) # 用来正常显示负号
k_values = [1, 2, 3, 4, 5, 6] # k的取值
x = np.linspace(-10, 10, 100) # x的范围
fig, axs = plt.subplots(2, 3, figsize=(10, 6)) # 创建2行3列的子窗口
for i, k in enumerate(k_values):
y = k * x ** 2 + 2 * k # 计算y值
row = i // 3 # 计算子窗口所在的行数
col = i % 3 # 计算子窗口所在的列数
ax = axs[row, col] # 获取当前子窗口
label = f'k={k}' # 设置标注
ax.plot(x, y, label=label) # 绘制曲线
ax.set_xlabel('x') # 添加x轴标签
ax.set_ylabel('y') # 添加y轴标签
ax.set_title(f'图 {i+1}') # 添加子窗口标题
ax.legend() # 添加图例
ax.grid(True) # 添加网格线
plt.tight_layout() # 自动调整子窗口布局
plt.show() # 显示图形
print("学号:3001")
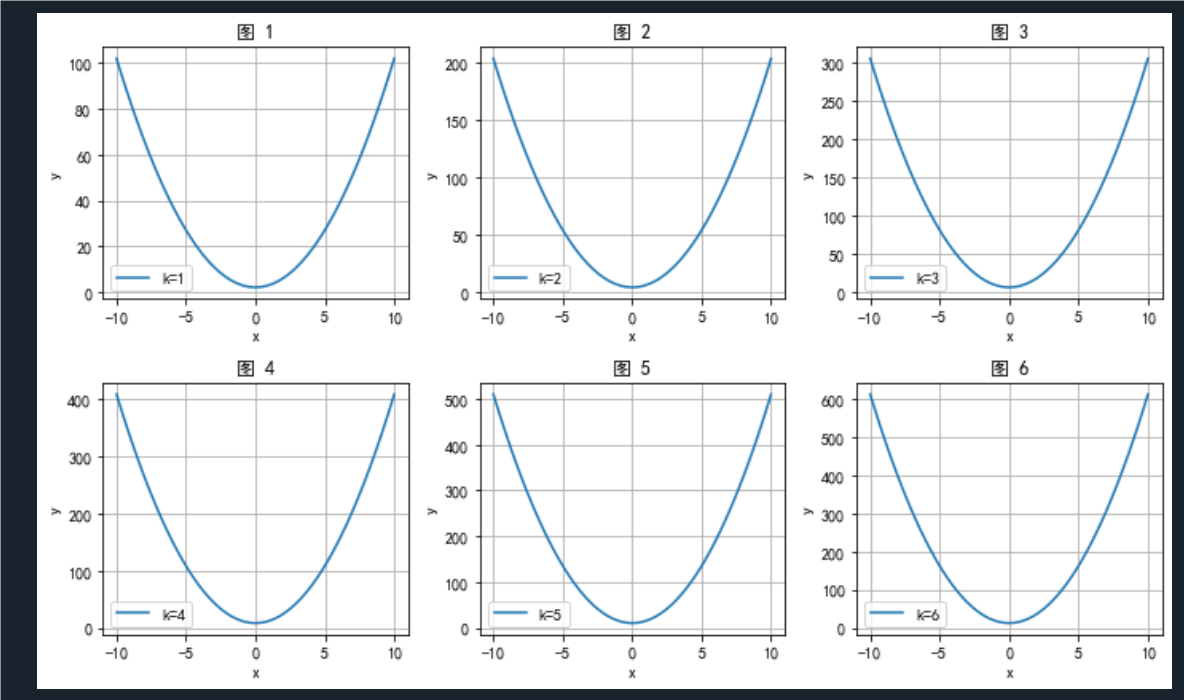
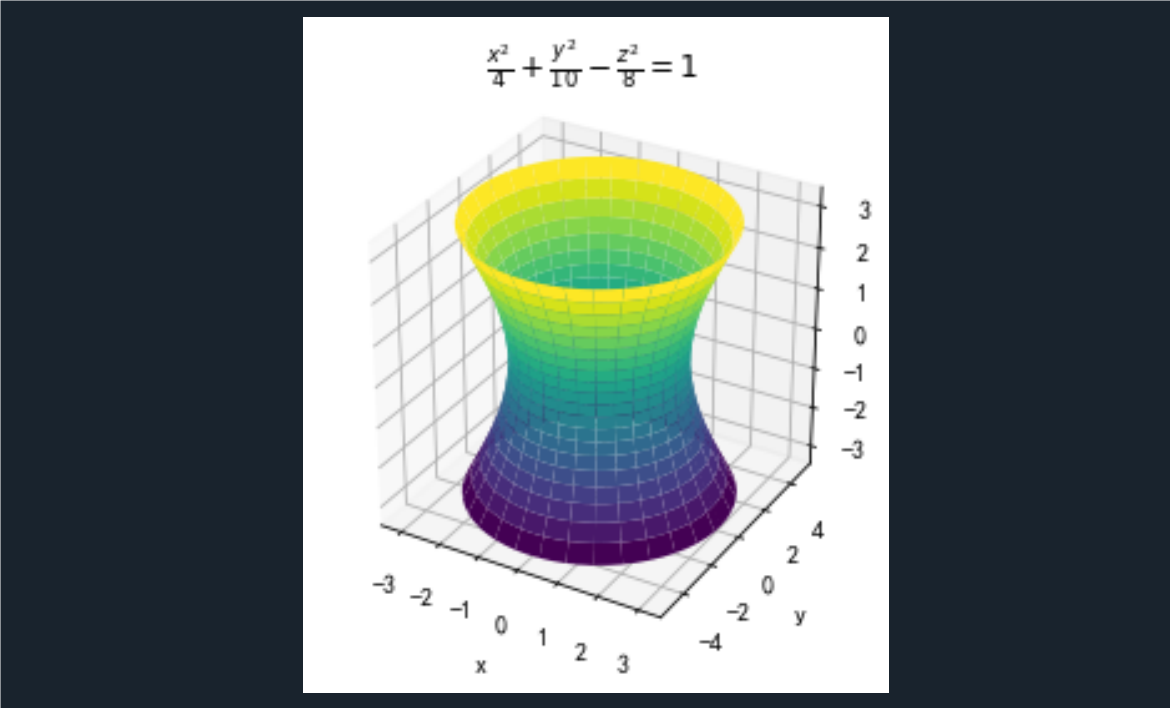
习题2.5
(1)
点击查看代码
import numpy as np
import matplotlib.pyplot as plt
a = 2
b = np.sqrt(10)
c = np.sqrt(8)
phi = np.arange(0, 2*np.pi+0.1, 0.1)
theta = np.arange(-1, 1.1, 0.1)[:, np.newaxis]
x = a * np.cosh(theta) * np.cos(phi)
y = b * np.cosh(theta) * np.sin(phi)
z = c * np.sinh(theta)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_box_aspect([1, 1, 1])
ax.set_title('$\\frac{x^2}{4}+\\frac{y^2}{10}-\\frac{z^2}{8}=1$')
plt.show()
print("学号:3001")
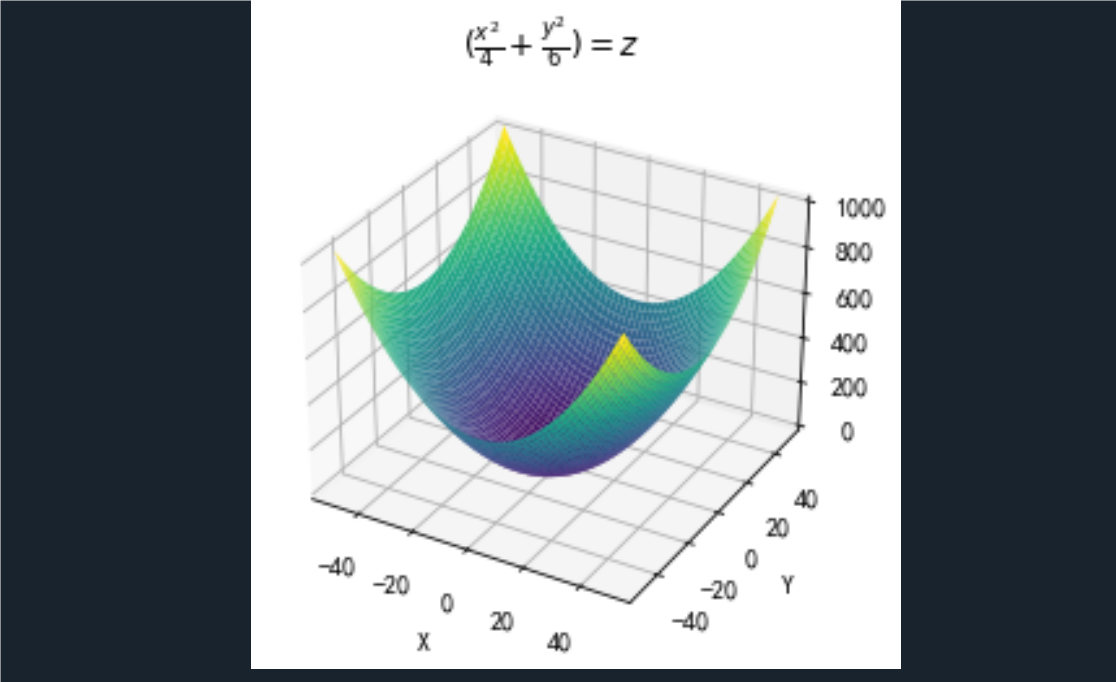
(2)
点击查看代码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 创建一个三维坐标系
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# 生成x,y的网格
x = np.linspace(-50, 50, 1000)
y = np.linspace(-50, 50, 1000)
X, Y = np.meshgrid(x, y)
# 计算z的值
Z = (X**2)/4+(Y**2)/6
# 绘制二次曲面
ax.plot_surface(X, Y, Z, cmap='viridis')
# 添加坐标轴标签
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# 添加标题
ax.set_title('$(\\frac{x^2}{4}+\\frac{y^2}{6})=z$')
# 设置z轴的范围
ax.set_zlim(0, 1000)
# 显示图形
plt.show()
print("学号:3001")
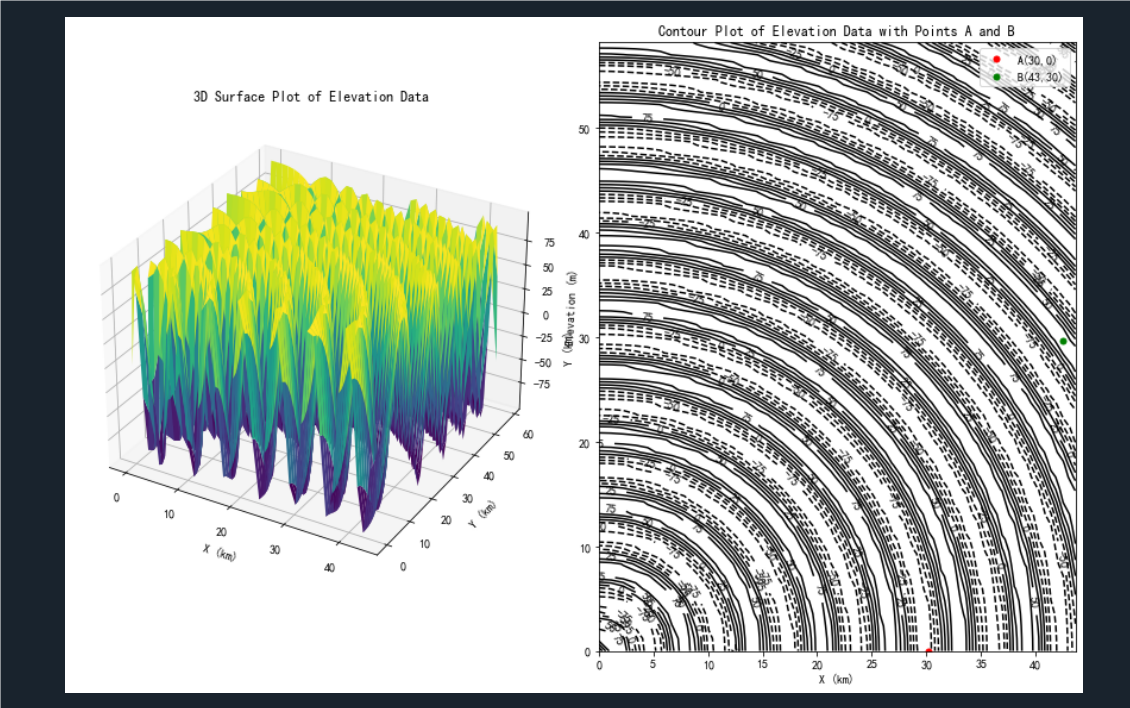
习题2.6
点击查看代码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 模拟高程数据(假设数据已经过某种方式插值或生成)
# 这里我们创建一个简单的40x50网格,并填充随机高程值
x = np.linspace(0, 43.65, 40)
y = np.linspace(0, 58.2, 50)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2)) * 100 # 使用一个简单的函数来生成高程数据
# 绘制三维表面图
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(121, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='none')
ax.set_xlabel('X (km)')
ax.set_ylabel('Y (km)')
ax.set_zlabel('Elevation (m)')
ax.set_title('3D Surface Plot of Elevation Data')
# 绘制等高线图
plt.subplot(122)
CS = plt.contour(X, Y, Z, colors='k')
plt.clabel(CS, inline=1, fontsize=10)
# 标注点 A(30,0) 和 B(43,30)
# 注意:由于X和Y是网格坐标,我们需要找到最接近这些值的索引
idx_a_x = np.argmin(np.abs(x - 30))
idx_a_y = np.argmin(np.abs(y - 0))
idx_b_x = np.argmin(np.abs(x - 43))
idx_b_y = np.argmin(np.abs(y - 30))
plt.plot(x[idx_a_x], y[idx_a_y], 'ro', markersize=5, label='A(30,0)')
plt.plot(x[idx_b_x], y[idx_b_y], 'go', markersize=5, label='B(43,30)')
plt.xlabel('X (km)')
plt.ylabel('Y (km)')
plt.title('Contour Plot of Elevation Data with Points A and B')
plt.legend()
# 计算地表面积的近似值(忽略地形起伏)
real_area = 43.65 * 58.2
print(f"Actual Surface Area (ignoring elevation changes): {real_area} km^2")
# 显示图形
plt.tight_layout()
plt.show()
print("学号:3001")
习题2.7
点击查看代码
import numpy as np
# 定义系数矩阵A和常数项向量b
A = np.array([[4, 2, -1],
[3, -1, 2],
[11, 3, 0]])
b = np.array([2, 10, 8])
# 使用numpy的lstsq求解最小二乘解
x, residuals, rank, s = np.linalg.lstsq(A, b, rcond=None)
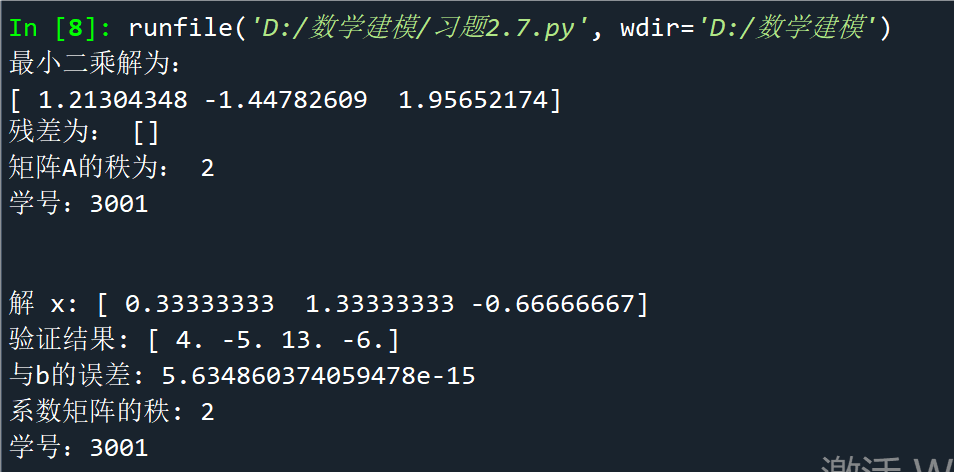
print("最小二乘解为:")
print(x)
# 打印残差和矩阵A的秩
print("残差为:", residuals)
print("矩阵A的秩为:", rank)
print("学号:3001")
print("\n")
import numpy as np
# 定义系数矩阵A和常数项向量b
A = np.array([[2, 3, 1],
[1, -2, 4],
[3, 8, -2],
[4, -1, 9]])
b = np.array([4, -5, 13, -6])
# 使用numpy的lstsq函数求解最小二乘解
# 对于这个特定的问题,由于方程数和未知数数量相同,且没有矛盾,lstsq将给出唯一解
x, residuals, rank, s = np.linalg.lstsq(A, b, rcond=None)
# 输出解
print("解 x:", x)
# 验证解是否正确(可选)
print("验证结果:", np.dot(A, x))
# 检查是否精确等于b(对于精确解,这应该非常接近)
print("与b的误差:", np.linalg.norm(np.dot(A, x) - b))
# 计算系数矩阵的秩(可选,以确认方程组是否有唯一解)
print("系数矩阵的秩:", np.linalg.matrix_rank(A))
# 由于秩等于未知数数量,且没有矛盾,我们可以确信有一个唯一解
print("学号:3001")
习题2.8
点击查看代码
import numpy as np
# 生成系数矩阵A
A = np.zeros((1000, 1000))
np.fill_diagonal(A, 4)
np.fill_diagonal(A[:, 1:], 1)
np.fill_diagonal(A[1:, :], 1)
# 生成常数向量b
b = np.arange(1, 1001)
# 判断解的情况
if np.linalg.matrix_rank(A) == np.linalg.matrix_rank(np.column_stack((A, b))):
if np.linalg.matrix_rank(A) == A.shape[1]:
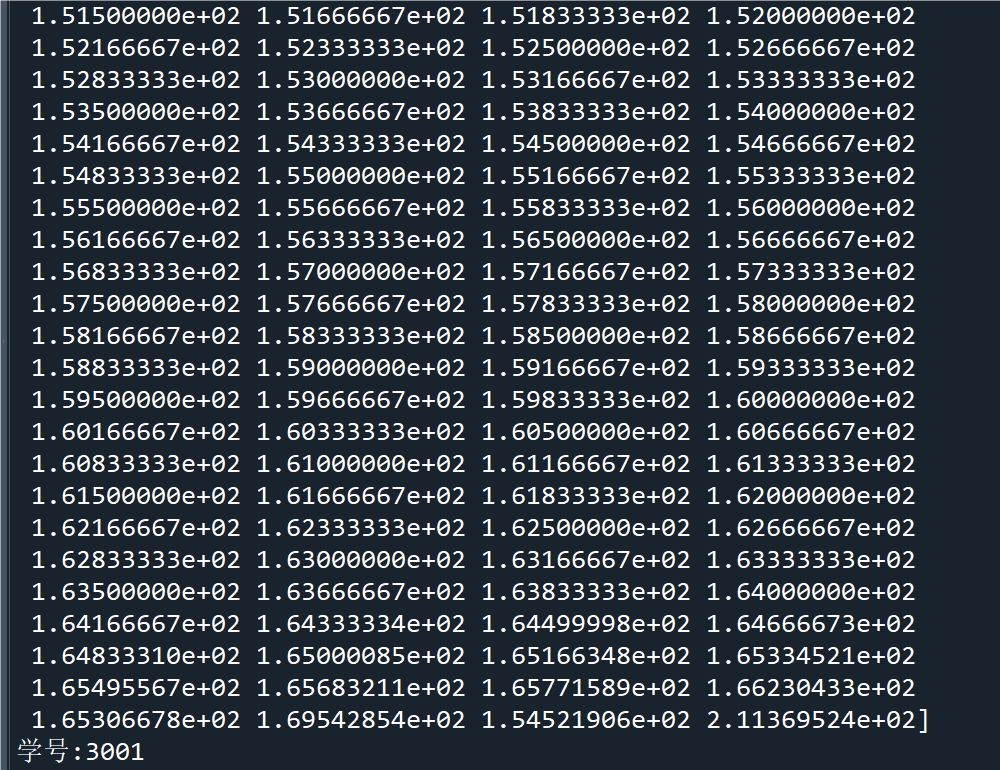
print("线性方程组有唯一解")
x_unique = np.linalg.solve(A, b)
print("唯一解 x =", x_unique)
else:
print("线性方程组有无穷多解")
x_least_squares = np.linalg.lstsq(A, b, rcond=None)[0]
print("最小二乘解 x =", x_least_squares)
else:
print("线性方程组无解")
x_least_squares = np.linalg.lstsq(A, b, rcond=None)[0]
print("最小二乘解 x =", x_least_squares)
x_min_norm = np.linalg.pinv(A).dot(b)
print("最小范数解 x =", x_min_norm)
import numpy as np
# 生成系数矩阵A
A = np.zeros((1000, 1000))
np.fill_diagonal(A, 4)
np.fill_diagonal(A[:, 1:], 1)
np.fill_diagonal(A[1:, :], 1)
# 生成常数向量b
b = np.arange(1, 1001)
# 判断解的情况
if np.linalg.matrix_rank(A) == np.linalg.matrix_rank(np.column_stack((A, b))):
if np.linalg.matrix_rank(A) == A.shape[1]:
print("线性方程组有唯一解")
x_unique = np.linalg.solve(A, b)
print("唯一解 x =", x_unique)
else:
print("线性方程组有无穷多解")
x_least_squares = np.linalg.lstsq(A, b, rcond=None)[0]
print("最小二乘解 x =", x_least_squares)
else:
print("线性方程组无解")
x_least_squares = np.linalg.lstsq(A, b, rcond=None)[0]
print("最小二乘解 x =", x_least_squares)
x_min_norm = np.linalg.pinv(A).dot(b)
print("最小范数解 x =", x_min_norm)
print("学号:3001")
习题2.9
点击查看代码
from sympy import symbols, Eq, solve
# 定义未知数
x, y = symbols('x y')
# 定义非线性方程组
equations = (Eq(x**2 - y - x - 3, 0), Eq(x + 3*y - 2, 0))
# 求解符号解
symbolic_solution = solve(equations, (x, y))
print("符号解:", symbolic_solution)
# 数值解需要使用数值方法求解
from scipy.optimize import fsolve
# 定义非线性方程组的函数
def equations(variables):
x, y = variables
return [x**2 - y - x - 3, x + 3*y - 2]
# 初始猜测值
initial_guess = [1, 1]
# 求解数值解
numeric_solution = fsolve(equations, initial_guess)
print("数值解:", numeric_solution)
print("学号:3001")

习题2.10
点击查看代码
from scipy.integrate import quad
import numpy as np
#抛物线旋转体
def V1_quad(y):
return np.pi * (4*y - y**2)
V1_corrected, _ = quad(V1_quad, 1, 3)
V2 = 0.5 * (4/3) * np.pi * 2**3 - (1/3) * np.pi * 2**2 * 1
# 计算总体积
total_volume_corrected = V1_corrected + V2
print("体积:",total_volume_corrected)
import numpy as np
import math
# 圆柱面部分
V2 = 4 * math.pi # 体积
y2 = 0.5 # 重心y坐标
# 假设水的密度 rho = 1000 kg/m^3
rho = 1000 # 水的密度
g = 9.81 # 重力加速度
# 计算重力势能变化和所需功
# 假设水被抽到无穷高(实际中可能有限制),这里以 y = 10(远大于容器高度)为例
final_y = 10
delta_E_p = rho * V2 * g * (final_y - y2)
W = delta_E_p
print(f"圆柱面部分所需功: {W} 焦耳")
print("学号:3001")

习题2.11
点击查看代码
import numpy as np
from scipy.optimize import fsolve
def f(x):
return (abs(x + 1) - abs(x - 1)) / 2 + np.sin(x)
def g(x):
return (abs(x + 3) - abs(x - 3)) / 2 + np.cos(x)
def equations(variables):
x1, x2, y1, y2 = variables[:4]
eq1 = 2 * x1 - (3 * f(y1) + 4 * g(y2) - 1)
eq2 = 3 * x2 - (2 * f(y1) + 6 * g(y2) - 2)
eq3 = y1 - (f(x1) + 3 * g(x2) - 3)
eq4 = 5 * y2 - (4 * f(x1) + 6 * g(x2) - 1)
return [eq1, eq2, eq3, eq4]
initial_guess = [0, 0, 0, 0] # 初始猜测值
numeric_solution = fsolve(equations, initial_guess)
print("数值解:", numeric_solution)
print("学号:3001")

习题2.12
点击查看代码
import numpy as np
from scipy.linalg import eig
# 定义矩阵
A = np.array([[-1, 1, 0],
[-4, 3, 0],
[1, 0, 2]])
# 计算特征值和特征向量
eigenvalues, eigenvectors = eig(A)
# 打印特征值
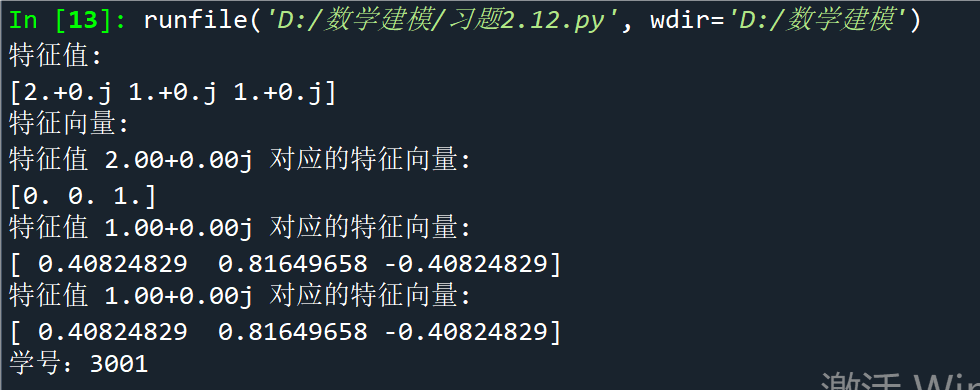
print("特征值:")
print(eigenvalues)
# 打印特征向量
print("特征向量:")
for i in range(eigenvectors.shape[1]):
print(f"特征值 {eigenvalues[i]:.2f} 对应的特征向量:")
print(eigenvectors[:, i].real) # 取实部,因为有时特征向量会有复数部分,但在这个特定例子中它们是实数
print("学号:3001")
习题2.13
点击查看代码
import numpy as np
from scipy.optimize import least_squares
def f(x):
return (np.abs(x + 1) - np.abs(x - 1)) / 2 + np.sin(x)
def g(x):
return (np.abs(x + 3) - np.abs(x - 3)) / 2 + np.cos(x)
def equations(variables):
x1, x2, y1, y2 = variables[:4]
eq1 = 2 * x1 - (3 * f(y1) + 4 * g(y2) - 1)
eq2 = 3 * x2 - (2 * f(y1) + 6 * g(y2) - 2)
eq3 = y1 - (f(x1) + 3 * g(x2) - 3)
eq4 = 5 * y2 - (4 * f(x1) + 6 * g(x2) - 1)
eq5 = x1 + y1 - (f(y2) + g(x2) - 2)
eq6 = x2 - 3 * y2 - (2 * f(x1) - 10 * g(y1) - 5)
return [eq1, eq2, eq3, eq4, eq5, eq6]
initial_guess = [0, 0, 0, 0] # 初始猜测值
result = least_squares(equations, initial_guess)
numeric_solution = result.x
print("最小二乘解:", numeric_solution)
print("学号:3001")
