SciTech-BigDataAIML-BP(BackPropagation反向传播)网络:“政经驱动”智慧星球城市的“BigData+Bitstream”+Org组织+“数学驱动”的“人+模型”
SciTech-BigDataAIML-BackPropagation反向传播:
“政治经济驱动”智慧星球城市的“BigData+Bitstream”
“数学驱动”的“人+模型”
Org组织
Computing Graph: 计算图
- Model模型四阶段:
-
Research研究:
源于一个Requirement需求,
转化为一系列的 Question/Problem问题,
明确好 Certainty + Uncertainty,
确定Goals+Strategies,
制定Plans: Data Collection, Available List of Models, Design of Experiments
执行Research + Plans:- Experiment 的 要点,流程化规范化
- 选定 Standard Dataset标准数据集,
- 总体筛选出最佳的 Models,统计概率,
-
Design设计: 确定最佳参数, 在研究选出的最佳模型上,确定 最佳模型parameters
-
Implement实现: 将“概念模型”工程化为“量产模型”
-
Application应用: 将“量产模型”部署应用“持续更新升级”
-
- Framework之上的“设计实现模型”,
如Google的Tensorflow, Meta的PyTorch, 提供并实现许多的Operators(标准组件),
Model Developers可对"积木标准件"拼积木, 得到"套路化"的"模型"的任意函数。 - Computing Graph: 计算图;
- 计算图上有"搭积木"的“Operators(算子, 标准件), 及相互之间连接的“IO张量网络”;
- Auto Gradient Machine, 自动梯度机, 涉及到本文的Backpropagation反向传播,
Backpropagation反向传播

Analysis of Mathmatics(数学分析学):
Measure Theory, 求Gradient偏导数,Integral积分, 多元
Advanced Linear Algebra 与 Matrix Analysis; 设计Tensor,Fields, Vector Space and Operations,
解方程组,
Probability + Statistics 概率论与统计学,将 Continues连续 和 Discrete离散的模型;
标准的
实现上有:Scipy, Numpy, Pandas, Matplotlib, Python, Anaconda, PyData,...
BP(Backpropagation)发的概念
BP(Backpropagation)依赖的是数学领域的PDE(Partial Differential Equation偏微分方程)
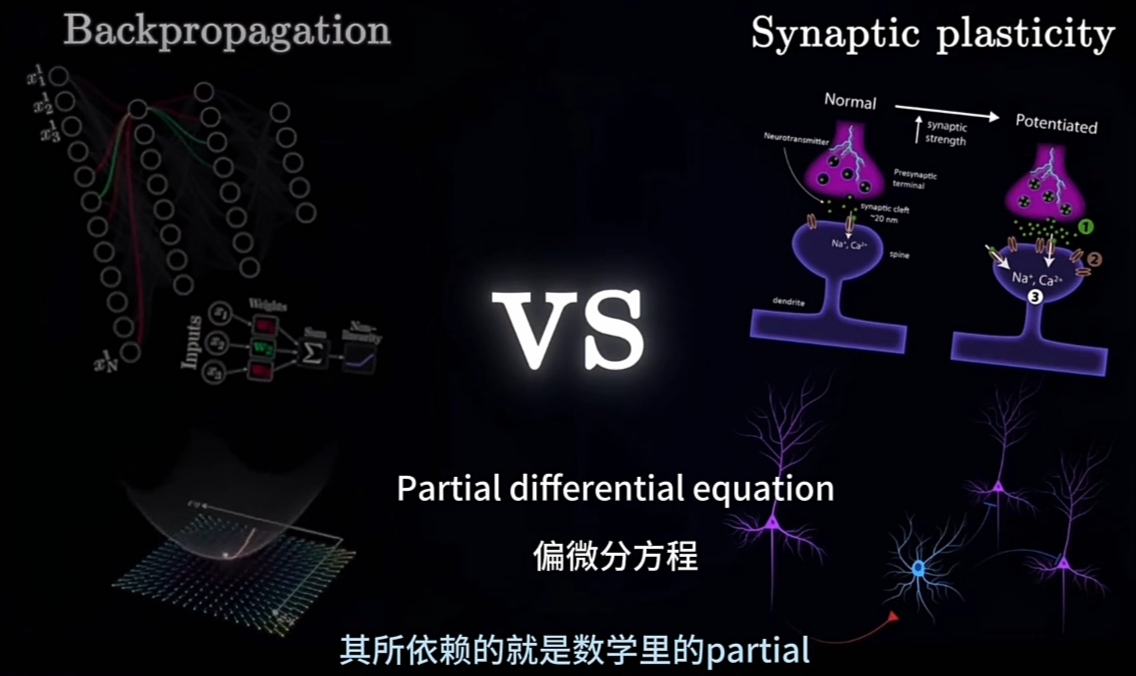
由GPT、Mid-Journey、AlphaFold到各种大模型,几乎所有的机器学习系统, 都有何共同点?
尽管他们为解决不同的问题而设计,有完全不同的架构,并在不同的数据集(库)上进行训练;
但有一些东西, 将所有这些不同系统联系在一起。在所有的这些不同模型系统,
都有一种BP(Backpropagation)算法, 在训练程序的模型内核运行.
BP(Backpropagation)是整个机器学习领域的基础. 所以深入研究就特别重要.

令人惊讶的是,人工神经网络有学习能力的原因,
也正是使他们与人类大脑的本质差异,和与生物学不相融的地方。

本视频是一个包含两部分的系列, 的第一部分. 今天探讨:
WHAT: 人工智能领域的反向传播概念,并直观的了解他是什么,
WHY: 为何有效,
HOW: 如何从无到有的构建这个算法,
BP(Backpropagation)的历史和里程碑
尽管backpropagation有变革的影响,但谁首先发明了BP却有多个版本:
- 因为BP用到的微分概念,最早可以追溯到17世纪的G.W. Leibniz(1676,莱布尼茨);
- BP算法的第一个现代表述,至今仍在使用,是由Seppo Linnainmaa在1970年发表的硕士论文(TAYLOR EXPANSION OF THE ACCUMULATED ROUNDING ERROR)提出的, 但是他并没有明确提到任何神经网络.
- 另一个重要里程碑在1986年:
- David Rumelhart, Geoffrey Hinton, Ronald Williams三人共同发布一篇名为"Lonely Representations by Backpropagating Errors"(反向传播的单独表示)的论文, 他们将BP算法应用于Multi-Layered Perceptrons(多层感知器,神经网络的一种); 并首次证明利用BP算法进行模型训练, 可使神经网络成功解决问题, 并在Hidden Layers(隐藏神经元层)开发出有意义的表示. 捕捉任务中的重要数据规律性.

- 值得一提的是, 2024的诺贝尔物理学奖就颁给David Rumelhart, Geoffrey Hinton。
- 随着这一领域的发展, 研究人员大幅扩展过这些模型, 并引入各种架构;
但训练基于BP算法的基本原则基本没有改变.
- David Rumelhart, Geoffrey Hinton, Ronald Williams三人共同发布一篇名为"Lonely Representations by Backpropagating Errors"(反向传播的单独表示)的论文, 他们将BP算法应用于Multi-Layered Perceptrons(多层感知器,神经网络的一种); 并首次证明利用BP算法进行模型训练, 可使神经网络成功解决问题, 并在Hidden Layers(隐藏神经元层)开发出有意义的表示. 捕捉任务中的重要数据规律性.
BP(反向传播)神经网络的概念构建.
为全面了解训练网络的确切含义,我们才尝试由头开始,
构建BP(反向传播)神经网络的概念.
导引问题:假设你搜集到一组"随机点序列", 要用最优函数拟合:
-
可用"数形结合"的方法进行直观的预先分析“随机点序列”;
将“随机点序列”描绘作图在“平面直角坐标系”上观察;
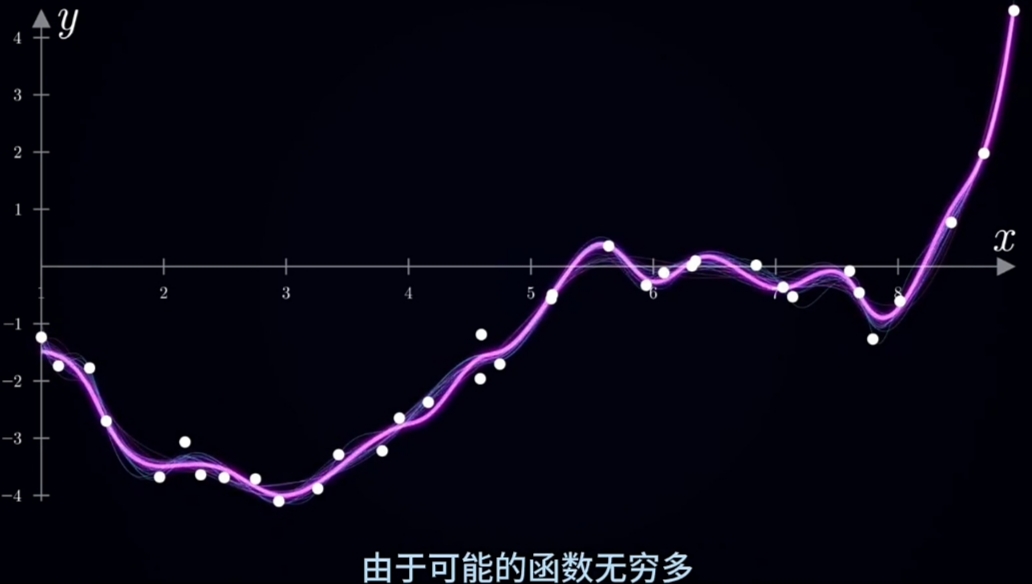
-
需要设置一组Hypothesis(假设)预筛选无限多的"可选拟和函数"。例如:
先用MSE(Mean Square Error)对无限多的可选“光滑拟和曲线”进行总体拟和精度评价估计(\(\large \mu均值, \ \sigma 标准差\));
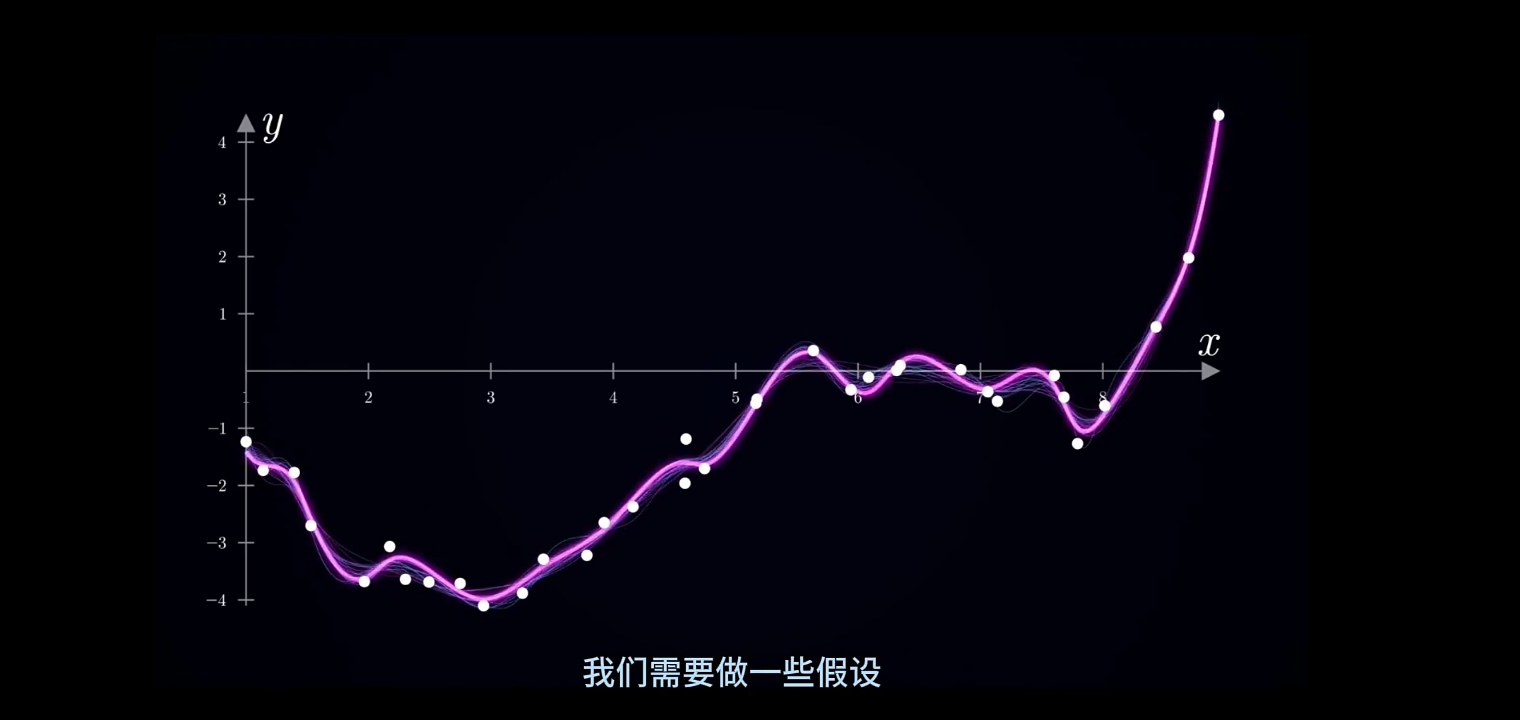
筛选出的"光滑拟和曲线"进行函数式拟和:
- 可用"高等代数学"的"eigen value decomposition"(主成分分解)将“离散点序列”分解为"eigen value matrix"
- 可用"数学分析学"的"泰勒公式拟和",Taylor拟和,的系数向量,做为参数;
- 可用"概率统计学"的"分布函数"进行"离散拟和", 复杂曲线用"分段函数"拟和,每一段都是基本的Distribution;
- 可用"复分析"及"Fourier Transform"进行"傅立叶函数拟和", 将Time Domian的光滑曲线分解为Freq Domain与一组参数;
- ...
可为"目标拟和函数"设定一组"预筛选条件":
- 选用"数学分析学"最经典的"Taylor Equation Approxmation"
-
确定"Taylor拟和"要用到的"最小最高幂次数"(\(\large 波峰数+波谷数+2\))
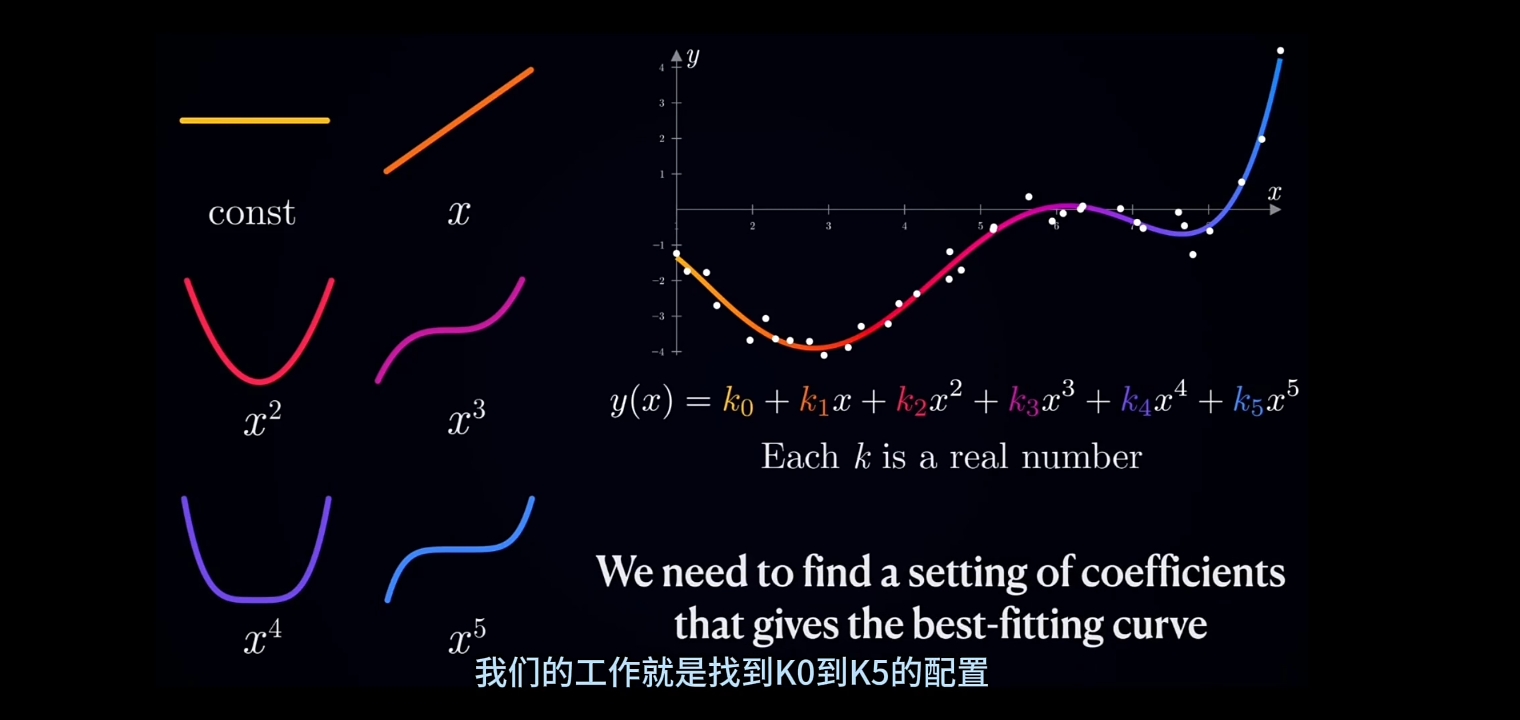
例如对上面的图例,"Taylor拟和"的"最小最高幂次数"可设置为5
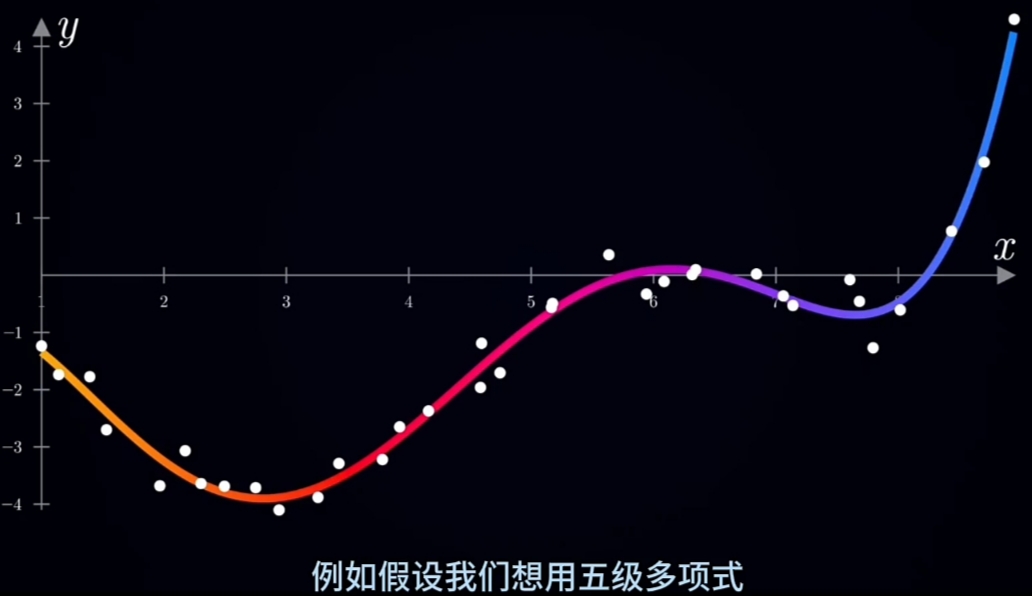
-
将"目标拟和函数"设定为“Taylor多项式形式”:
\(\large \begin{array}{ll} y=f(x) & = \overset{\rightarrow}{K} \cdot \overset{\rightarrow}{X^T} \\ &= (k_0, k_1, k_2, k_3, k_4, k_5) \cdot (x^0, x^1, x^2, x^3, x^4, x^5)^T \\ &= k_0 + k1_x^1+ k_2x^2+ k_3x^3+ k_4x^4+ k_5x^5 \\ \end{array}\)
接着的工作就是确定参数向量\(\large K\): $\large (k_0, k_1, k_2, k_3, k_4, k_5) $
-
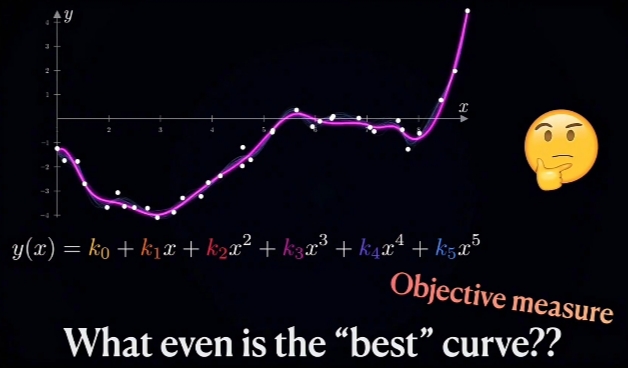
\(\large Measure\ Similarity\) 度量相似度 OR \(\large Embedding\)(嵌入):
任意两点,度量这两点的Similarity:
KL Divergence, Euclidian Distance, Cosine Similarity, ...
-
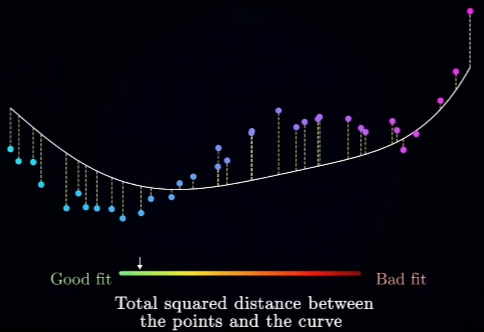
Loss Function(Relation + Quantity, 量化"拟和质量"为一"数值"):
用一个Loss Function表达式(用Similarity和多项式表示)建立数学模型;

"MSE(Mean Square Error,均方损失函数)"是最经典的(写入各大主流高等教育的数学教科书)之一.- 采集Sample(有代表性, 样本点足够多): 假设样本容量为n, 则Sample为:
\(\large X =\{(x_1, y_1),\ (x_2, y_2),\ \cdots\ (x_n, y_n)\}\) - 对每个采样点\(\large (x_i, y_i)\),计算其方差值\(\large S_{x_i}\)( 真实值(\(\large y_i\) 与 "拟和函数"在\(\large x_i\)处的函数值\(\large LF(x_i)\) 的差值(Error)的平方(Square)数:
\(\large S_{x_i} = (LF(x_i) - y_i)^2\) - 计算"拟和质量"的总量化数值:加和样本\(\large X\) 的全部采样点的方差值
\(\large \begin{array}{rl} MSE_{X} &= \overset{n}{\underset{i=1}{\sum}} {S_{x_i}} = \overset{n}{\underset{i=1}{\sum}} {(LF(x_i) - y_i)^2},\ where,\\ X &=\{(x_1, y_1),\ (x_2, y_2),\ \cdots\ (x_n, y_n)\} \\ \end{array}\)
常用的还有: - "KL Divergence"(两个Distribution的),
- "Euclidian Distance(距离)",
- "Cosine Similarity(距离+角度)",
- 其它
- 采集Sample(有代表性, 样本点足够多): 假设样本容量为n, 则Sample为:
-
s
-
http://krz.github.io/backpropagation-explained/
Backpropagation from the ground up:
In this video we will introduce the core algorithm powering all of Machine learning and build it from first principles