Python 学习记录（1）

hai-zei / 2024-11-11 / 原文

前言

简单说明：

简单情况：主要记录学习Python的简单情况，包括代码与结果，以及关键注释
工具与来源：以下代码与结果都可在JupyterLab上实现，更多情况可看Github

使用 NumPy 可视化数学函数

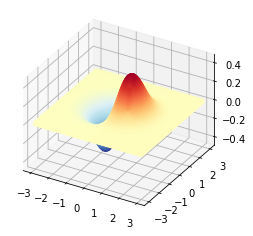
1.可视化 f=x1*e(-x1^2-x22)

import numpy as np
import matplotlib.pyplot as plt

x1_array=np.linspace(-3,3,121)

#其中生成从-3，到 3 的121个数据的数组

x2_array=np.linspace(-3,3,121)

xx1,xx2=np.meshgrid(x1_array,x2_array)

#利用meshgrid函数生成网格化数据（二维数组,前后分别表示x,y轴;xx1,xx2都是二维数组)

ff=xx1*np.exp(-xx1**2-xx2**2)

#得出函数值，也是一个二维数组，表示的是对用点的数值

fig=plt.figure()
#创建一个图形对象
ax=fig.add_subplot(projection='3d')
#使用add_subplot()方法添加一个三维轴对象

ax.plot_wireframe(xx1,xx2,ff,
                  rstride=1,cstride=100,
                  color='grey')
ax.scatter(xx1,xx2,ff,c=ff,cmap='RdYlBu_r')

#在三维轴上绘制散点图

ax.set_proj_type('ortho')
#角度
plt.show()

结果图片：

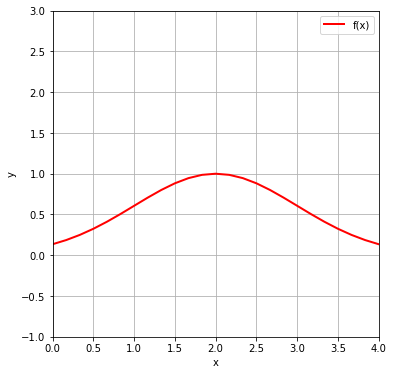
2.可视化 f(x)=e^( -(x-2)^2 /2)

import numpy as np
import plotly.express as px
import matplotlib.pyplot as plt

x_array=np.linspace(-10,10,121)
y_array=np.exp(-((x_array-2)**2/2))

#同上

fig,ax=plt.subplots(figsize=(8,6))

#同时给出图像，坐标轴对象，其中“窗口”宽8，高6.（英寸）

ax.plot(x_array,y_array,
        label='f(x)',color='r',linewidth=2)

#直接用plot方法绘画

ax.set_xlabel('x')
ax.set_ylabel('y')

#添加标签

ax.legend()

#添加图像解释

ax.set_xlim(0,4)
ax.set_ylim(-1,3)

#设置取值范围

ax.set_aspect('equal')
#表示相等
plt.grid()

#添加网格

plt.show()

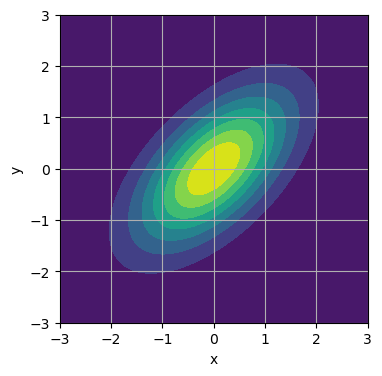
3.可视化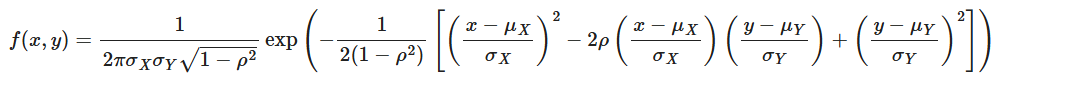

其中 μx=0,μy=0,δx=1,δy=1,ρx,y=0.6

import numpy as np
import matplotlib.pyplot as plt

sigma_X = 1
sigma_Y = 1
rho_XY  = 0.6
mu_X    = 0
mu_Y    = 0

def f_XY_PDF(xx1, xx2, sigma_X, sigma_Y, rho_XY, mu_X, mu_Y):
    coeff = 2 * np.pi * sigma_X * sigma_Y * np.sqrt(1 - rho_XY**2)
    coeff = 1/coeff
    xx1_ = (xx1 - mu_X)/sigma_X
    xx2_ = (xx2 - mu_Y)/sigma_Y
    
    ellipse = 1/(1 - rho_XY**2) * (xx1_**2 - 2*rho_XY*xx1_*xx2_ + xx2_**2)
    PDF = coeff * np.exp(-1/2 * ellipse)
    
    return PDF

x1_array = np.linspace(-3, 3, 301)
x2_array = np.linspace(-3, 3, 301)
xx1, xx2 = np.meshgrid(x1_array, x2_array)
PDF_ff = f_XY_PDF(xx1, xx2, sigma_X, sigma_Y, rho_XY, mu_X, mu_Y)


fig, ax = plt.subplots(figsize=(4, 4))
ax.contourf(xx1, xx2, PDF_ff)

ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)    
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.grid()
ax.set_aspect('equal', adjustable='box')

结果：