python第五章课后习题

5227abc / 2024-11-07 / 原文

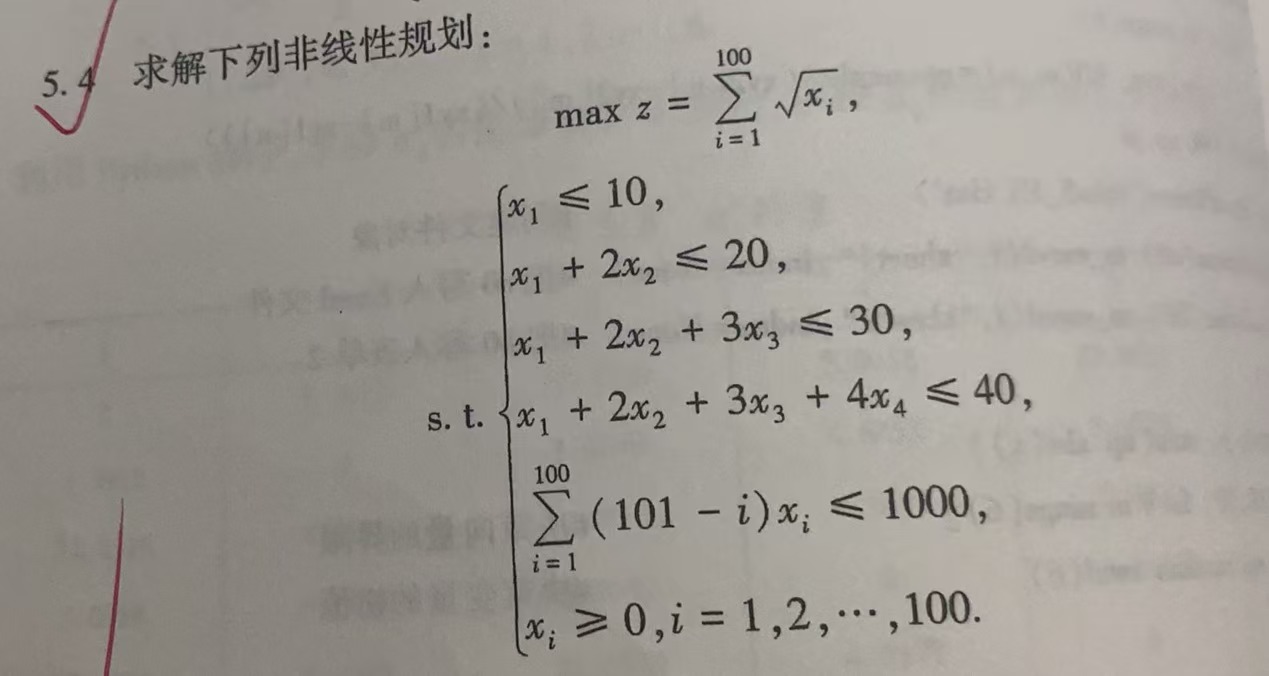
import numpy as np

import math

from scipy.optimize import minimize,Bounds

def func(x):

return sum(math.sqrt(x[i]) for i in range(100))

def con(x):

return 1000-np.sum(x[i]*(101-i+1) for i in range(100))

con1={'type':'ineq','fun': lambda x: 10-x[0]}

con2={'type':'ineq','fun': lambda x: 20-x[0]-2*x[1]}

con3={'type':'ineq','fun': lambda x: 30-x[0]-x[1]2-x[2]3}

con4={'type':'ineq','fun': lambda x: 40-x[0]-x[1]2-x[2]3-x[3]*4}

con5={'type':'ineq','fun': con}

cons=[con1,con2,con3,con4,con5]

bounds=Bounds([0]100,np.inf100)

res=minimize(func,np.random.randn(100),constraints=cons,bounds=bounds)

print(res.x)

print(res.fun)

import numpy as np
from scipy.optimize import minimize
def objective(x):
return - (2 * x[0] + 3 * x[0]2 + 3 * x[1] + x[1]2 + x[2])
def con1(x):
return 10 - (x[0] + 2 * x[0]2 + x[1] + 2 * x[1]2 + x[2])
def con2(x):
return 50 - (x[0] + x[0]2 + x[1] + x[1]2 - x[2])
def con3(x):
return 40 - (2 * x[0] + x[0]2 + 2 * x[1] + x[2])
def con4(x):
return x[0] + 2 * x[1] - 1
def con5(x):
return x[0]
def con6(x):
return x[0]2 + x[2] - 2
cons = ({'type': 'ineq', 'fun': con1},
{'type': 'ineq', 'fun': con2},
{'type': 'ineq', 'fun': con3},
{'type': 'ineq', 'fun': lambda x: -con4(x)},
{'type': 'ineq', 'fun': lambda x: con5(x)},
{'type': 'eq', 'fun': con6})

x0 = np.random.rand(3)
bounds = [(0, None) for _ in range(3)]
solution = minimize(objective, x0, method='SLSQP', bounds=bounds, constraints=cons)
print('Optimal solution:', solution.x)
print('Objective value at optimal solution:', -solution.fun)

runfile('C:/Users/ddrrg/.spyder-py3/PYTHON2/习题5.7.py', wdir='C:/Users/ddrrg/.spyder-py3/PYTHON2')

点击查看代码

demand_list = [40, 60, 80]  
max_prod = 100  
total_demand_sum = sum(demand_list)    
dp_table = np.full((4, total_demand_sum + 1), float('inf'))  
dp_table[0][0] = 0  
  
prev_prod_plan = np.full((4, total_demand_sum + 1), -1)  
  
for period in range(1, 4):  
    prev_demand_total = sum(demand_list[:period])  
    for demand_met in range(total_demand_sum + 1):  
        if demand_met < prev_demand_total + demand_list[period - 1]:  
            continue  
        for production in range(max(0, demand_met - prev_demand_total - demand_list[period - 1] + 1),  
                                min(max_prod + 1, demand_met - prev_demand_total + 1)):  
            prod_cost = 50 * production + 0.2 * production ** 2  
            storage_cost = 4 * (demand_met - prev_demand_total - production)  
            total_expense = dp_table[period - 1][demand_met - production] + prod_cost + storage_cost  
            if total_expense < dp_table[period][demand_met]:  
                dp_table[period][demand_met] = total_expense  
                prev_prod_plan[period][demand_met] = production  
  
min_expense = float('inf')  
final_demand_met = -1  
for demand_met in range(total_demand_sum, total_demand_sum + 1):  
    if dp_table[3][demand_met] < min_expense:  
        min_expense = dp_table[3][demand_met]  
        final_demand_met = demand_met    
production_schedule = [0] * 3  
current_demand_met = final_demand_met  
for period in range(3, 0, -1):  
    production_schedule[period - 1] = prev_prod_plan[period][current_demand_met]  
    current_demand_met -= prev_prod_plan[period][current_demand_met]    
print(f"最小总费用为: {min_expense} 元")  
print("生产计划为:")  
for period, plan in enumerate(production_schedule, 1):  
    print(f"第{period}季度生产: {plan} 台")  
print("学号：3028")


print("学号：2023310143028")

最小总费用为: 11280.0 元生产计划为: 第1季度生产: 50 台第2季度生产: 60 台第3季度生产: 70 台学号：3028