矩形
- 矩形
- 应用
- 应用1:Leetcode.223
- 题目
- 解题思路
- 代码实现
- 应用场景
- 应用1:Leetcode.850
- 题目
- 解题思路
- 代码实现
- 应用1:Leetcode.223
- 应用
矩形
应用
应用1:Leetcode.223
题目
223. 矩形面积
给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形,请你计算并返回两个矩形覆盖的总面积。
每个矩形由其 左下 顶点和 右上 顶点坐标表示:
-
第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。
-
第二个矩形由其左下顶点 (bx1, by1) 和右上顶点 (bx2, by2) 定义。
示例 1:
输入:ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出:45
解题思路
两个矩形覆盖的总面积等于两个矩形的面积之和减去两个矩形的重叠部分的面积。
由于两个矩形的左下顶点和右上顶点已知,因此两个矩形的面积可以直接计算。如果两个矩形重叠,则两个矩形的重叠部分也是矩形,重叠部分的面积可以根据重叠部分的边界计算。
两个矩形的在坐标轴上的投影:
-
水平边投影到 \(x\) 轴上的线段分别为 \([a_{x1},\ a_{x2}]\) 和 \([b_{x1}, b_{x2}]\) ,
-
竖直边投影到 \(y\) 轴上的线段分别为 \([a_{y1}, a_{y2}]\) 和 \([b_{y1}, b_{y2}]\)。
如果两个矩形重叠,则对于重叠部分:
-
水平边投影到 \(x\) 轴上的线段为 \([max(a_{x1}, b_{x1}), min(a_{x2}, b_{x2})]\);
-
竖直边投影到 \(y\) 轴上的线段为 \([max(a_{y1}, b_{y1}), min(a_{y2}, b_{y2})]\)。
根据重叠部分的水平边投影到 \(x\) 轴上的线段长度和竖直边投影到 \(y\) 轴上的线段长度,即可计算重叠部分的面积。
注意:只有当两条线段的长度都大于 0 时,重叠部分的面积才大于 0,否则重叠部分的面积为 0。
代码实现
class Solution:
def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:
# 先求重叠部分的长和宽
x = max(0, min(ax2, bx2) - max(ax1, bx1))
y = max(0, min(ay2, by2) - max(ay1, by1))
# 总面积=两个矩形的面积 - 重合部分的面积
return (ax2 - ax1) * (ay2 - ay1) + (bx2 - bx1) * (by2 - by1) - x * y
应用场景
应用场景:目标检测计算 IOU(Intersection over Union)。
应用1:Leetcode.850
题目
850. 矩形面积 II
给你一个轴对齐的二维数组 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐标, (xi1, yi1) 是该矩形 左下角 的坐标, (xi2, yi2) 是该矩形 右上角 的坐标。
计算平面中所有 rectangles 所覆盖的 总面积 。任何被两个或多个矩形覆盖的区域应只计算 一次 。返回 总面积 。因为答案可能太大,返回 \(10^9 + 7\) 的 模 。
示例 1:
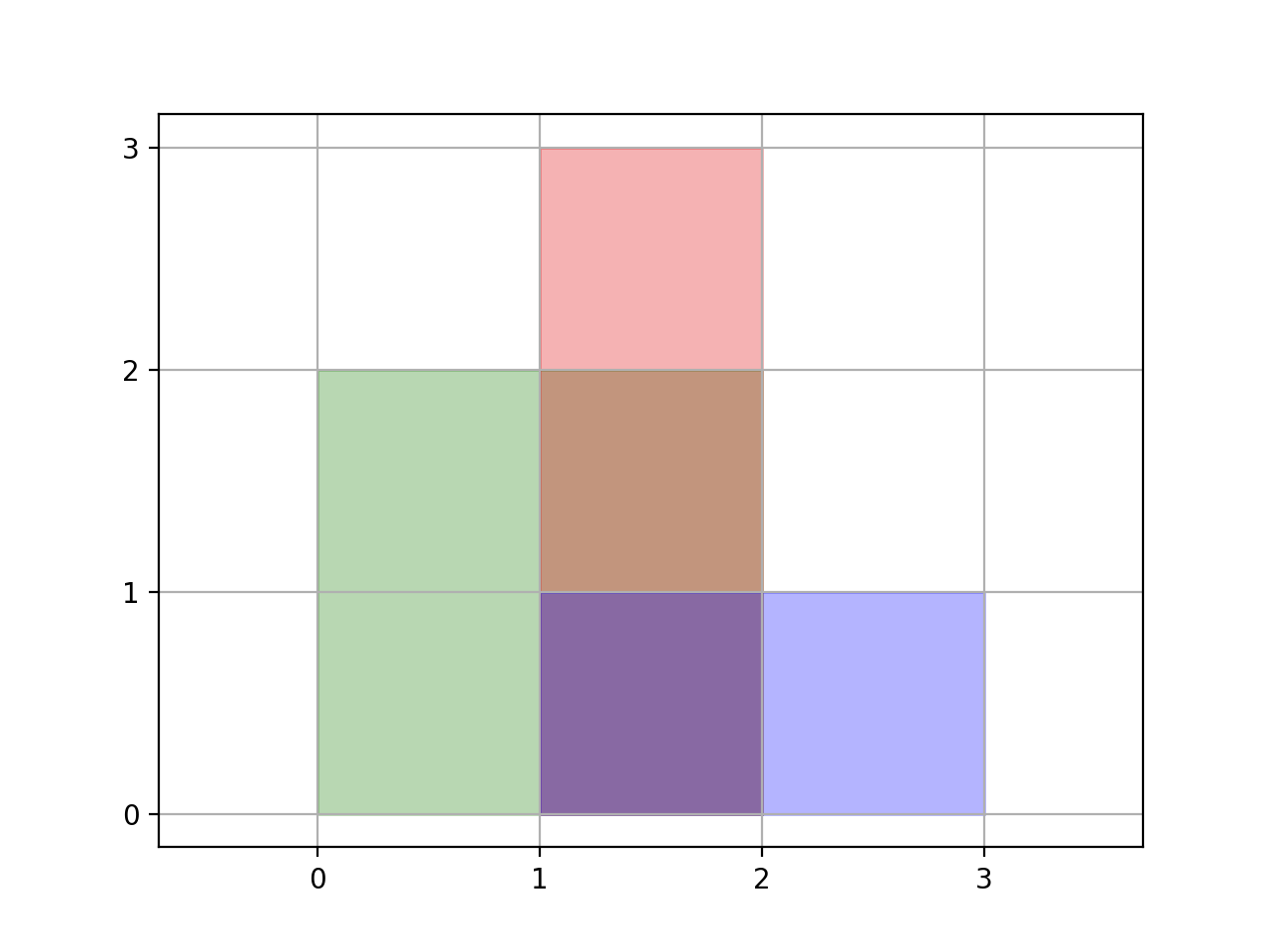
输入:rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出:6
解释:如图所示,三个矩形覆盖了总面积为 6 的区域。
从(1,1)到(2,2),绿色矩形和红色矩形重叠。
从(1,0)到(2,3),三个矩形都重叠。
解题思路
代码实现