一维差分模板

xie-blog / 2025-02-21 / 原文

一维差分模板

题目描述:

输入一个长度为 n的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r]之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式:

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式:

共一行，包含 n 个整数，表示最终序列。

数据范围:

1≤n,m≤100000
1≤l≤r≤n
−1000≤c≤1000
−1000≤整数序列中元素的值≤1000

输入样例:

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例:

3 4 5 3 4 2

差分，可以看作对前缀和的逆运算，差分和前缀和类似于求导和积分的关系。

首先我们有一个数组,a[0],a[1]........a[n-1],a[n]

然后我们可以构建另一个数组,b[0],b[1].........b[n-1],b[n]

将a数组看作是b数组的前缀和数组，也就是:a[i]=b[0]+......+b[i-1]+b[i]。

那么b数组就是a数组的差分数组。

如图所示:

知道了差分数组有什么用呢?让我们往后看。

回到题目,题目要求我们在区间[l,r]内的每个数都加上c,询问m次，我们正常的暴力做法是:

for(int i=l;i<=r;i++)
{
     a[i]+=c;
}

这个时间复杂度是O(n)的，但是我们可以用差分将这个时间复杂度优化到O(1).

我们要想到一点，a数组是b数组的前缀和数组,也就是对b数组的操作，会同样的影响到a数组。

首先，我们可以先让b[l]+c..........b[r]+c,

这样就给[l,r]内的数加上了c,

然后还没有结束,

我们还需要,b[r+1]-c..........b[n]-c

为什么要这样呢?

我们可以画图理解:

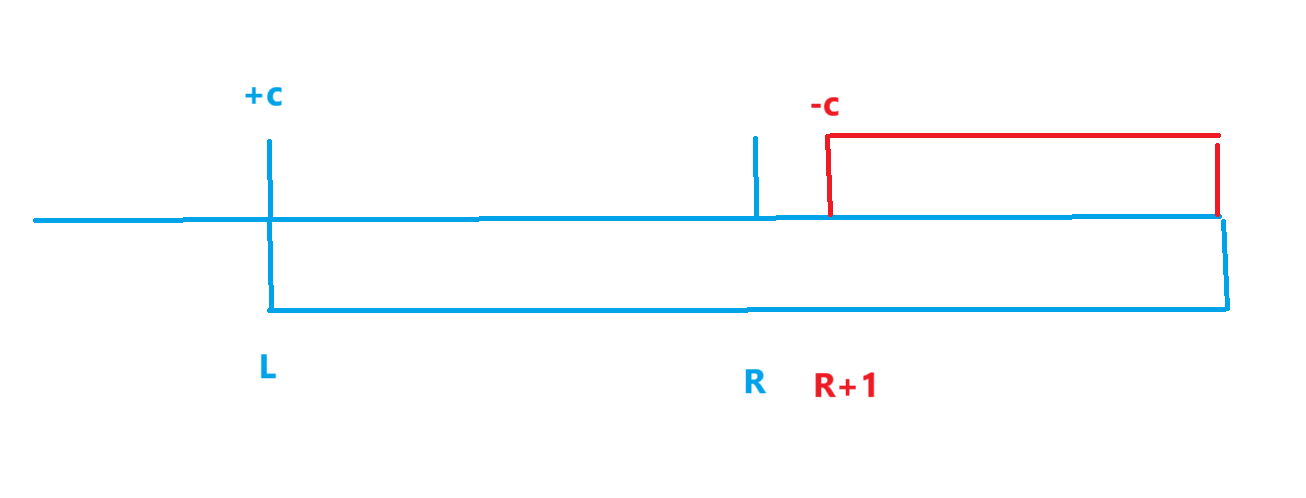
如果我们给b[l]+c,那么从l到n内的所有数都会+c,那我们该怎么做呢?

那我们只要给R+1到n内的所有数再减上c不就行了吗?

于是我们就得到了一维差分的核心代码:

b[l]+=c;
b[r+1]-=c;

完整代码如下:

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int a[N],b[N];  //a是原数组，b是差分数组 
int n,m;
  //差分操作 
void insert(int l,int r,int c)
{
	b[l]+=c;
	b[r+1]-=c;
}
int main()
{
	scanf("%d%d",&n,&m);
	
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	
	for(int i=1;i<=n;i++) insert(i,i,a[i]);     //构建差分数组 
	
	
	//询问 
	while(m--)
	{
		int l,r,c;
		scanf("%d%d%d",&l,&r,&c);
		insert(l,r,c);  //[l,r]对每个数进行加c操作
		               //O(1)的时间复杂度 
	}
	 
	 //将b数组还原为a数组 
	for(int i=1;i<=n;i++) a[i]=a[i-1]+b[i];
	
	for(int i=1;i<=n;i++) printf("%d ",a[i]);
	
	return 0;
 }