随便刷的题part1
数组基础题目&二维数组基础题目
数组
189.轮换数组(special)
分析:
像队列一样,不过出去的要放在队头。第一感觉是将前面n个元素补在后面再裁剪数组。
解法:
1、将前面n个元素补在后面再裁剪数组
2、反转数组,找到旋转节点,再次反转节点左右部分数组(巧妙方法)
3、创建新数组,找到旋转节点填充新数组,最后赋值给原数组(额外的空间,思路比较直接)
4、交错换位法,纯数学推导方法,懒得想,知道有这个方法就好
66. 加一
分析:
第一感觉就是从后向前推呗,遇到9就进位,然后在下一位加一再次判断,可以递归。
解法:
1、从后向前推呗,遇到9就进位,然后在下一位加一再次判断,可以递归。类似逆向的builtin_popcorn
2、没有2这道题极其简单,但是从评论区看到了很多刚学习算法的小可爱吐槽自己这种题都做不出来,好怀念啊
724.寻找数组的中心下标(op)
分析:
因为涉及左右之和,一眼看出来是前缀和的启蒙题,第一反映是用两个数组分别存放前缀后缀然后比较。
解法:
1、用两个数组分别存放前缀后缀然后比较
2、可以优化第一种做法,因为要满足pre_sum = reverse_pre_sum,可以先求出数组总和sum,再根据当前前缀和求后缀和。假设当前位置为i,则有sum - nums[i] - pre_sum[i] = reverse_pre_sum,得到sum - nums[i] = 2 * pre_sum[i]。嗯就是利用现有已记忆数据推导另外的数据,小优化。
485.最大连续1的个数
分析:
连续个数,一般都会想到双指针贪心,我也是这么做的,不过进行了小小的优化。
解法:
1、建立临时变量temp,遇到1则加一,遇到0则置零,每次加一都更新结果。
2、在评论区看到了一个同学的写法,思考了几分钟后才发现思路是一样的只是res : i = temp ? temp++ :0这里因为他没加括号,我在对符号前后顺序不熟的情况下产生了歧义。
238.除自身以外数组的乘积
分析:
前后缀和(积),感觉也没啥技巧,和724几乎一模一样
解法:
1、左右乘积数组
2、用原数组当左前缀积数组的左右数组乘积法
二维数组
498.对角线遍历(moni)
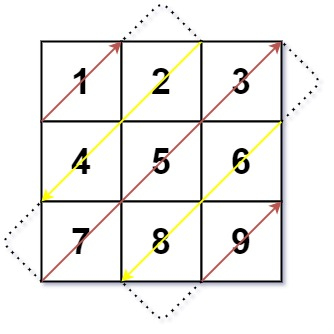
分析:
强行模拟其实也可以,不过一定的规律可以极大地减少边界条件的处理。
解法:
1、方向无非是右上或左下,在对角线前边界转弯时是向下向右走,在对角线或过了对角线是向右向下走。即不同方向过边方向在对角线处反置了。我们只需要判断其是否走到了边界,其走的方向是什么,其走到了第几个对角线。小tip是对角线数量为m+n-1。模拟,没什么说的,分解问题然后组装在一起喽。
2、官方题解和我思路一样,写法不一样,懒得看啦。
48.旋转图像(special)
分析:
很有趣的题,结合了坐标变换,开始其实是观察发现要不要试试以中间点为中央对称点直接进行坐标变换。
解法:
1、使用辅助数组,没什么说的,按顺序遍历就行,没什么可说的,用这个方法的属实是没办法的办法。
2、两次反转,上下左右反转,妙妙屋QAQ
3、原地旋转,坐标映射。提示:在4x4矩阵中,旋转过程中(0,0)->(0,3),(1,0)->(0,2)即旋转过程中行列关系存在一个公式,即after_rotate[j][k-i-1] = before_rotate[i][j]。得到这个规律,判断一下这个矩阵需要遍历几层,然后顺时针调转四个坐标的值即可,期间需要一个临时值temp做交换的中间数。(另外三个坐标持续用第一个公式推导即可)
73.矩阵置零(op)
分析:
比较经典的状态记录题,一开始想直接A掉,用二维数组记录哪行哪列有0,然后再第二次扫描时进行整体置零。这样空间时间都是O(n^2),非常垃圾。
解法:
1、用二维数组记录哪行哪列有0,然后再第二次扫描时进行整体置零。这样空间时间都是O(n^2),非常垃圾。
2、用两个一维数组分别记录行列是否有0,然后再进行第二次遍历进行置零。空间变成n了,时间还是O(n^2)
3、用矩阵的第一行第一列来替代方法二中的两个标记数组,如果当前行列有0直接将当前0所在行列第一个数置0,在第二次遍历时查看行列是否为0进行置零即可。
4、只用一个标记变量来记录第一列是否有0,第一行是否有0直接用(0,0)记录,由于本质上还是用第一行第一列记录状态,而且第一行不能先被覆盖,于是从最后一行向前遍历,当然,从第二行向后遍历结果也是一样的。