SCP-S总结
没交代码啊,肯定没交蛤。
这是不好的,下次尽量。
T1 P11188 「KDOI-10」商店砍价

是不是不太好想?
没事,后面看数据范围,有惊天秘密
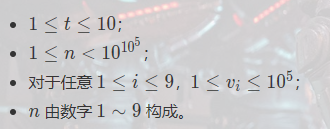
你什么 $v_i$ 这么小,才1e5?一般不都有1e9吗
其实破题的关键就在这里了,算是一种比较另类的考虑方式(我太菜了)
就是您去想想最极端的情况,就算全部都单删,那那$n>10^6$的时候,也肯定比整删划算了!
也就是说,剩余数位的长度不超过6。如果要留数位来整删,那最多只能留6个,其他都得单删。
那直接dp完事。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+1;
int c,t,v[N],f[N][6];
char s[N];
signed main(){
cin>>c>>t;
while(t--){
cin>>s+1;
int n=strlen(s+1);
for(int i=1;i<=9;++i)
cin>>v[i];
int ans=0,mins=0;
memset(f,0x3f,sizeof f);
for(int i=1;i<=n+1;++i)
f[i][0]=0;
for(int i=n;i>=1;--i){
ans+=v[s[i]-'0'];//处理普通情况
for(int j=1;j<=5;++j)
f[i][j]=min(f[i+1][j],f[i+1][j-1]+(int)pow(10,j-1)*(s[i]-'0')-v[s[i]-'0']);//当前是选择遗传下来还是当开头
}
for(int i=n;i>=1;--i)
for(int j=1;j<=5;++j)
mins=min(mins,f[i][j]);
cout<<ans+mins<<endl;
}
return 0;
}代码复制的我看的第一篇题解。我来写的话估计不会这么写,但是也就凑合着看吧。
说真的,这个题,把我坑惨了。真的没有想到,完全没有往这方面去想过,真的。
第一次看数据做题,下次长记性。
T2 P11189 「KDOI-10」水杯降温
这是个紫啊,放到T2了,不过也没什么问题不大
一眼树上差分(不是,哥,你别骂我,他都成这个样子了,谁不会想到树上差分,你不会还要老老实实地一次次去操作)(当然你说在递归上动手脚,那我确实不太会)

嗯,虽然不太好一下子全部分析完,但是一步步来还是可以的,不难理解(比较难想就是了)(其实这个题说是比较板子,那我正好趁机学习了)
那么就,嗯,就这样呗。把两个操作都转化了,就不用再考虑原树值了。
然后有了差分的树,我们很愉快地得出了我们需要的结果:全部变成0。在最后成功的时刻,根节点要是0的;他的儿孙们,每个都跟前面的一样,自然也都是0了。
其实这样的话,都不需要考虑俩操作的顺序了。不过还是说一下,有很多做法都是钦定先做操作二再做操作一;其实是一个比较好的思路。遇到这种操作与顺序无关的时候,这样想一下是有出路的。
那 $nw$值是负的,还不好办嘛,操作一加加就0了。但是说真的,如果$nw>0$,那就不好办了。只有根节点啊,他的$nw$值才可以变小,别的无论如何都变大。所以其他节点大于零了直接无解。根节点大于0,我们怎么办呢?
那这个很神秘地想到了树上DP。即,从子树往上推。
直观感受到,任意 $u$ 子树(在操作二以$u$为根时)存在一个操作次数上限,超过它会使得某些节点的$nw$值变得大于0,我们就没有办法了。所以不能超过次数上限。
设$f[u]$表示以$u$为根的子树的操作上限。当我们考虑$u$时,我们已经求出了他的儿子们的$f$值。
现在,我们需要在$u$这里进行操作。每次操作肯定要从其中一个儿子那里上来嘛。经过这个儿子和$u$,其他儿子不在路径上但与路径直接相连,$nw$值需要加一。
我们需要确保的是,在每个儿子节点的$nw$值都不大于零,并且从每个儿子上来的操作次数不大于其$f$值的前提下,把这个操作次数最大化。
可以转化为如下问题:

其中$d$就是$nw$。(另外一篇题解截的图)
又可以转化为,每次从每一堆里面都拿一个出来,再选择一堆放回去。这样不好办,我们发现正如上文所述,“从每一堆中拿一个出来”和“选择一堆放回去”,其实操作的结果和顺序无关。那么完全可以分开看。如果操作次数为$k$,那么可以先把所有的$n$d堆石子都拿$k$个;现在的石子堆里可能有正有负。然后,我们还有$k$次可以选择一堆放回去一个的机会。如果这$k$次可以把那些变成负数的堆全部填回去,并且每一堆被填的次数不大于其$f$值,那么在此子树中进行$k$次操作就是可行的。
显然,$k$具有单调性,因而直接想到二分。上界就是根节点还差多少到0。(都可以把根节点减到零了,还做更多的事情干啥?而且有些子树上界是$+ \infty$的)
那最后根节点的$f$值就是整棵树最多能够执行的操作二次数了。如果说还不足以把根节点减成0,那就无解了。
#include "bits/stdc++.h"
#define int long long
#define rep(i,k,n) for(int i=k;i<=n;++i)
#define per(i,n,k) for(int i=n;i>=k;--i)
using namespace std;
template<typename T>
inline void read(T &x){
x=0;int f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c-'0');
x*=f;
}
const int N=1e6+10,INF=1e12;
int c,T;
int n,a[N],f[N];
vector<int> g[N];
bool ck(int u,int mid){
int sum=0,sum2=0;
for(auto v:g[u]){
int need=max({0ll,mid-(a[u]-a[v])});
if(need>f[v]) return 0;
sum+=need;
}
return sum<=mid;
}
void dfs(int u){
if(!g[u].size()){f[u]=INF;return;}
int l=0,r=0;
for(auto v:g[u]){dfs(v),r+=f[v];}
while(l<=r){
int mid=(l+r)>>1;
if(ck(u,mid)) l=mid+1;
else r=mid-1;
}
f[u]=r;
}
void solve(){
read(n);
rep(i,1,n) g[i].clear();
rep(i,2,n){
int fa;read(fa);
g[fa].push_back(i);
}
rep(i,1,n) read(a[i]);
rep(i,1,n) for(auto v:g[i]){
if(a[i]<a[v]){printf("Shuiniao\n");return;}
}
dfs(1);
if(f[1]<a[1]){printf("Shuiniao\n");return;}
else{printf("Huoyu\n");return;}
}
signed main(){
read(c);read(T);
while(T--) solve();
return 0;
}哦对了,这个题读入量大,需要快读。输出?看上去比较少,cout应该没问题。
T3 P11190 「KDOI-10」反回文串

好吧,一开始还看成子串了
但是不管如何,看到这种,都想着尽可能每一个子序列都只分两个字符。
下面有两个特殊性质,是引导我们破题的关键。
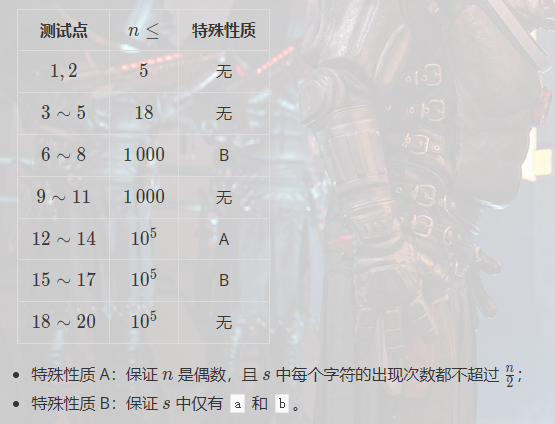
诶,为什么说,每个字符出现的次数都不超过一半呢?这就是经典的绝对众数问题思想了。如果有一个数的出现次数超过了序列长度的一半,则称其为绝对众数。
P2397 yyy loves Maths VI (mode) 这个题可谓是相当好(ban)蛙(zi)。他告诉我们一件事,如果一个序列存在绝对众数,那么把所有不同的数全部两两配对后,还会有剩下的——那就是序列的绝对众数。反之,如果没有剩下,则不存在绝对众数。很妙的trick。
这个题,基本上来说,就是这个trick的延伸吧。还评了个蓝。
不过不知道的话确实比较难想。而且延伸的idea也还不错,值得点赞。


娓娓道来。比较细致地分析。其实可以看到,主要就是考虑怎么把不同的配对以及剩下的相同的数合理处置的方式。差不多就是这样,不再赘述。

????????????
第一次见过这么6的,正解离30分只有一步之遥。但实际上,15分的A性质还好,接下来B性质的分析还是思维量比较大的。
但是真的就是这样,B性质就真的跟其他情况没啥区别了!其实也都是之前那个橙题,绝对众数的思想。只要把他处理好了,剩下不同的两两组合都好办。
但是如果你不知道这个trick,那麻烦就大了。
好题,好题。
P11191 「KDOI-10」超级演出
第一眼看到题,感到奇(hai)怪(pa)。倒像不像的图论给了一个序列,还让操作....
但其实仔细思考后发现,既然操作都是要从序列的某个子段开始从左到右操作的,而且一个点必须前面的走完了才能走,就想到暑假写的那个csp2023的t4好像有点异曲同工之处....一个点如果可以被操作,那必定在序列中他的前面存在一个点,使得至少要从这个点开始选择,他才能够操作。

这差不多就出来了。
对于$w_i$的求出,我比较偏向于使用队列去遍历该图。(然后好像还需要用spfa去迭代?)反正,先初始化每个点的$w$为-INF。其实可以去遍历$a$数组,然后如果是直达1就是$i$。如果不是就从他的所有后继(前驱?)中寻找max。然后如果直达的点重复出现了,是可以upd的。
这段话说的可能有点乱,但就是这样的。但其实还有个问题,有点节点度数可能非常大(这一点就不是我能够考虑到的了)所以有了根号分治的做法。

这段话就说的很清楚了。度数大的不管,度数小的在处理时前驱后继一并处理。
然后就是非常typical的二维数点问题了。这对我来说虽然是个新trick,但在这里并不详细赘述,会放在另外一篇里面。该怎么做怎么做即可。
#include<bits/stdc++.h>
inline int lowbit(int x){
return x&-x;
}
int bit[200005];
int k;
inline void add(int x,int y){
for(++x;x<=k;x+=lowbit(x))bit[x]+=y;
}
inline int ask(int x){
static int res;res=0;
for(++x;x;x^=lowbit(x))res+=bit[x];
return res;
}
std::vector<int>v[200005],e[200005];
bool sig[200005];
int nxt[200005];
int l[200005];
std::vector<std::pair<int,int> >g[200005];
int ans[200005];
int lst[200005];
int a[200005];
int n,m,q,lim;
int main(){
scanf("%*d%d%d%d%d",&n,&m,&k,&q);
lim=sqrt(m);
for(int x,y;m--;)
scanf("%d%d",&x,&y),
v[x].push_back(y),
sig[x]|=y==1;
for(int i=1;i<=n;++i)
if(v[i].size()>lim)
for(const int&j:v[i])
e[j].push_back(i);
for(int i=1;i<=k;++i){
scanf("%d",&a[i]);
if(sig[a[i]])l[i]=i;
else if(v[a[i]].size()<=lim)
for(const int&j:v[a[i]])
l[i]=std::max(l[i],lst[j]);
else l[i]=nxt[a[i]];
lst[a[i]]=l[i];
for(const int&j:e[a[i]])
nxt[j]=std::max(nxt[j],l[i]);
}
for(int i=1,l,r;i<=q;++i)
scanf("%d%d",&l,&r),
g[r].emplace_back(l,i);
memset(lst,0,sizeof(lst));
for(int i=1;i<=k;++i){
add(l[lst[a[i]]],1);add(l[i],-1);
lst[a[i]]=i;
for(const auto&j:g[i])
ans[j.second]=n-1-ask(j.first-1);
}
for(int i=1;i<=q;++i)
printf("%d\n",ans[i]);
return 0;
}实际上,跟t2一样,作为紫题,他的每一个子问题,每一个part,思维难度都是不小的。想到对于每个点存在$w_i$,本身就是不容易的一步;想到如何去转移,求出,又是一个子问题;如何去优化避免菊花图,需要用到根号分治这种trick;最后变成二维数点问题,本身也算比较进阶的问题模型了。但可能也正是因为子问题多,特殊性质和部分分也多。这样的特殊性质很可能是某个单独的子问题,即弱化或不考虑其他子问题的情况;最后通过这样一个个的子问题推导出正解。t3尤其如此。所以重视部分分、特殊性质,也许就是出题人在引导你推出正解。
好了写完了。第一次把S组的四个题全部弄完。不对,第一次把一场比赛的四个题全部弄完。还是很值得纪念的。
撒花✿✿ヽ(°▽°)ノ✿