摘要

时间序列聚类通过在线时间的变化对观看次数进行聚类，可以识别出随时间演变计数模式相似的动画系列，这可能有助于公司降低他们的投资风险。对于动画观看次数的时间序列数据，大多数现有的时间序列聚类方法忽略了数据内部的局部关系和数据之间的全局关系，这使得识别具有相似演变模式的动画系列变得具有挑战性。因此，我们提出了一种两阶段的深度图聚类方法，包括图数据构建和深度图聚类。具体来说，图数据构建将时间序列数据转换为图数据，而深度图聚类则使用时序卷积网络和图卷积网络分别从时间序列数据和图数据中学习特征。整个模型然后端到端训练以完成聚类任务，利用双重自监督模块。本研究使用两个数据集来评估我们提出的模型与基线方法的聚类性能。数据集包括2018年至2022年腾讯视频上185个动画系列的观看次数数据，以及一个公共的时间序列BME数据集。实验结果表明，我们的模型在两个数据集上都优于基线方法。此外，通过可视化识别的三种演变模式，我们为动画企业提出了新的产品开发策略。

1.introduction

时间序列是按时间顺序获得的一组观测数据，广泛存在于生产和日常生活中，例如产品销售数据、居民用电量数据、信号处理数据、互联网浏览行为数据等。 近年来，许多数据挖掘技术已应用于时间序列数据，包括聚类[1]、分类[2]、预测[3]和异常检测[4,5]。 聚类作为一种无监督方法引起了相当多的关注，并已应用于解决许多领域的各种问题。 例如，在能源领域，它被用来识别家庭的主要用电模式[6]； 在金融领域，用于发现不同股票价格之间相同的变化模式[7]； 在互联网领域，它被应用于探索在线内容的网络流行模式[8]。 时间序列聚类可以通过从复杂数据集中识别潜在模式来提取有价值的信息以支持决策。
动画系列在数字文化新业态中已十分普遍，并逐渐成为网络环境下成长的新一代消费者的主流文化产品[9]。 消费者可以通过Netflix、AbemaTV、腾讯视频等在线流媒体平台随时轻松便捷地观看动画剧集。 然而，由于动画系列中剧集的播放时间不同，每集的观看次数存在显着差异。 例如，在腾讯视频平台，《完美世界》第一集的播放量为9489.1万，而第七集的播放量仅为3662.4万； 同样，《唯我论》第一集的观看次数为1017.2万次，而第七集的观看次数为2316.3万次。 此外，动画系列之间的总观看次数显示出很大的差异。 例如，截至2021年底，《完美世界》的观看次数接近26.7亿次，而《唯我论》的观看次数只有4亿次[10]。 动画系列中各集观看次数的差异导致动画系列之间的总观看次数存在显着差异。 更重要的是，不同动画系列的观看次数呈现出不同的演变模式。 具体来说，进化模式是指随着动画系列剧在线总集数的增加，每集的观看次数发生变化，导致剧集的观看次数序列在动画系列的生命周期中呈现出特定的波动趋势。 例如，某些动画系列剧集的观看次数序列显示出持续下降的趋势，而另一些动画系列中的观看次数则持续上升。 因此，有必要利用聚类方法来识别具有相似进化模式的动画系列。 这些方法可以帮助动漫公司有效了解客户行为，进一步洞察客户需求，从而在后期选择、发布动漫产品、确定动漫投资等方面做出更好的决策。 此外，聚类方法可以为探索不同进化模式的原因提供基础。
然而，由于剧集的连续性质，动画系列内的剧集的观看计数序列构成了典型的时间序列数据（即，动画观看计数数据的时间序列）。 此外，这种类型的时间序列数据显示出巨大的波动性，并且前后的值不明确[11,12]，这使得它容易出现异常值和噪声。 因为前后几集的叙事质量和主题多样性[13]严重影响了观看次数。 对于动画观看次数（TS-AVC）数据的时间序列，局部和全局关系都存在。 局部关系反映了单个动画系列中各集之间观看次数的显着差异，而全局关系则反映了不同动画系列中总观看次数的显着变化。 因此，从数据的角度来看，我们不仅需要考虑局部关系，还需要考虑全局关系来提高TS-AVC数据聚类的性能。
另一方面，目前对时间序列数据聚类方法的研究大致可以分为两类：基于原始数据的方法和基于特征的方法[14]。基于原始数据的方法主要提出了各种相似性度量，如欧几里得距离（ED）[15]、动态时间规整（DTW）[16]和基于形状的距离（SBD）[17]。然而，它们只考虑使用相似性度量来实现时间序列中时间点之间的局部关系，而不是时间序列之间的全局关系。此外，这些方法通常对异常值和噪声敏感，这使得减少它们的影响变得具有挑战性。相比之下，基于特征的方法提出了不同的特征表示，如主成分分析（PCA）[18]、自适应分段常数近似（APCA）[19]和符号聚合近似（SAX）[20]。它们将原始时间序列从一个高维特征空间映射到一个低维潜在空间以执行聚类。尽管如此，它们主要手动表示时间序列特征，依赖于领域知识，导致特征表示能力有限。而时间序列深度聚类在数据特征学习方面可以是有效的。例如，Madiraju等人[21]使用自编码器和聚类层来学习非线性聚类表示。聚类层是通过测量预测和目标分布之间的KL偏差来设计的。在训练过程中，目标分布是从预测分布计算出来的，并在每次迭代中更新，这可能导致不稳定。Ma等人[22]使用序列自编码器来学习时间序列数据的隐藏向量表示，并添加了一个伪样本鉴别器来提高聚类效果。由于时间序列深度聚类的聚类分布是基于学习到的表示来计算的，编码器的能力严重影响聚类性能。同时，它们没有考虑时间序列之间的全局关系。此外，在特征表示过程中，随着数据量的减少，失真程度增加。因此，在大多数基于特征的方法中，有效地平衡降维和数据失真之间的关系是一个挑战。
先前的考虑支持需要进一步探索时间序列聚类。 具体来说，这项工作有两个动​​机。 首先，面对动画时间序列数据的差分特征，我们必须同时考虑时间序列的局部关系和全局关系。 如果我们仅仅依靠基于原始数据或基于特征的方法，我们就无法充分考虑数据之间的关系。 其次，如果数据关系得到充分关注，相似性度量和时间卷积网络（TCN）都可以捕获数据中的局部关系[23]。 此外，图神经网络（GNN）可以从图数据中提取全局关系[24]。 因此，从方法的角度来看，我们应该同时考虑相似性度量和特征表示来提高聚类性能。
基于上述观察，我们提出了一种 TS-AVC 深度图聚类方法（TDGC），该方法具有适当的相似性度量和有效的特征表示，以考虑 TS-AVC 数据中的局部和全局关系。 所提出的方法是一个两阶段的聚类框架，包括图数据构建和深度图聚类（图1）。

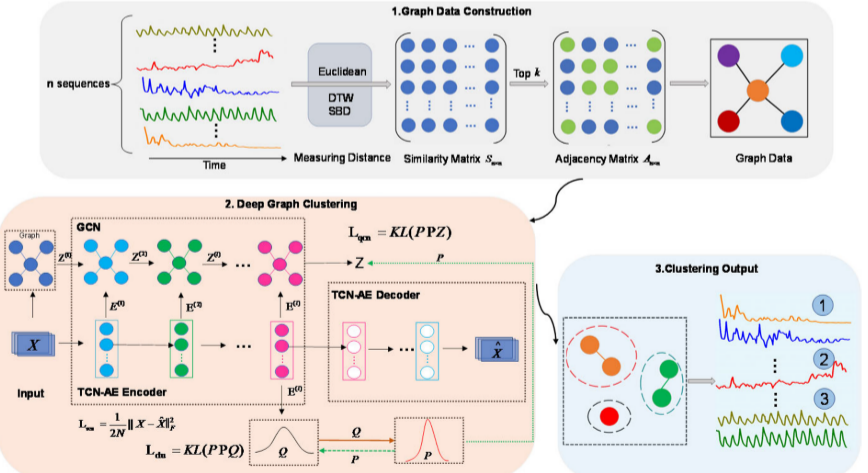
图1：该框架主要包括两个阶段：图数据构建和深度图聚类。 在图数据构建阶段，通过序列之间的相似性测度形成相似度矩阵Sn×n，然后通过选择相似度矩阵每行中最近的k个元素并分配剩余的元素来构建邻接矩阵An×n 元素为1和0组成∧图数据。 在深度图聚类阶段，X表示原始时序数据的特征矩阵。 X^表示TCN-AE编码器的重配置结果。 l 代表网络的第l层。 E(l)表示TCN网络的高维特征学习结果。 Z(l)表示GCN网络的高维特征学习结果。 Q表示聚类结果的分布，P是根据Q计算的。P和Q构成双自监督模块。 分布结果P和Q构成损失函数，用于更新整个网络的参数。
（1）在第一阶段，我们使用相似性度量从 TS-AVC 数据构建动画视图计数 (G-AVC) 数据图。 每个TS-AVC数据由一个节点表示，并且使用距离函数度量构造节点之间的边以形成G-AVC数据。 此阶段考虑 TS-AVC 数据内的局部关系以及为时间序列数据选择适当的相似性度量的重要性。
（2）在第二阶段，我们集成了图卷积网络（GCN）模块和TCN-AE模块，以充分表征G-AVC数据的结构信息和TS-AVC数据的特征信息。 为了以统一的方式指导 GCN 和 TCN-AE 模块的输出表示，我们通过双自监督模块使整个模型能够以端到端的方式针对聚类任务进行训练。 此阶段考虑 TS-AVC 数据之间的全局关系以及时间序列数据的有效特征表示学习的重要性。
总之，两阶段聚类TDGC方法巧妙地感知了时序数据内部的局部关系和时序数据之间的全局关系，有效地在降维和数据失真之间建立了平衡。 而且，它不仅是相似性度量和特征表示方法的集成，而且是数据自适应和算法自适应的集成。 具体来说，TDGC方法具有以下三个优点。
（1）使用相似性度量将时间序列数据转换为图数据可以帮助深入了解时间序列数据的全局关系并改进聚类。 同时，构建的图数据已经包含了原始数据之间的相似关系，可以输入到GCN模块中学习结构特征，从而构成二次聚类过程。 这是因为图数据的邻居节点往往具有相似的特征，使得深度图聚类阶段的邻居节点更倾向于处于同一簇中[25]。这种二次聚类过程不仅通过神经网络模块高效地学习数据特征，而且有效地平衡了降维和数据失真之间的关系。
（2）TCN-AE模块可以充分学习原始时间序列数据的特征，并减少相似性度量中异常值和噪声的影响。 因为深度神经网络（DNN）无法捕获相邻时间序列之间的语义关系，而 TCN 可以更有效地捕获相邻时间序列之间的语义关系。
(3)两个阶段是相辅相成的。第一阶段提供图形数据来支持第二阶段，构建的图形数据的质量对深度图聚类阶段有很大影响。 深度图聚类的第二阶段可以弥补第一阶段传统聚类方法的缺陷。
总的来说，本研究的贡献如下。 首先，本研究提出了一种TS-AVC数据的聚类方法，并验证了其效率和实用性。 此外，该方法的可扩展性在公共时间序列BME数据集上得到验证，丰富了现有的时间序列聚类方法，为未来的研究提供新思路。 其次，基于所提出的聚类方法，TS-AVC 的进化模式被识别和可视化。 结果表明存在三种不同的进化模式，为更深层次挖掘动画系列特征信息提供支持。 第三，分析了三种不同演化模式的动画系列特征的共性和差异，为动画企业的新产品开发提供有益的决策支持。

2.相关工作

2.1 略

2.2 时序聚类方法

时间序列聚类方法大致可以分为两种方法：基于原始数据的方法和基于特征的方法[14]。基于原始数据的方法也被称为基于形状的方法。这类方法直接处理原始时间序列数据，尝试通过时间轴的非线性拉伸和压缩尽可能匹配两个时间序列的形状。它们通常依赖于传统的聚类方法，例如使用静态数据，允许它们的距离或相似性度量被修改以适应时间序列。Petitjean等人[30]提出了一种结合DTW和K-means的K-DBA方法。Yang等人[31]提出了一种K-谱质心（K-SC）方法，该方法使用对时间序列的缩放和平移不变的相似性度量来实现聚类。Paparrizos等人[17]介绍了一种称为K-shape的方法，通过归一化交叉相关相似性度量和一种保留时间序列形状的质心计算方法来执行聚类。虽然这些方法捕捉了时间序列数据点之间的数值相似性，并考虑了时间点之间的局部对应关系，但它们没有考虑数据之间的全局关系。此外，它们通常对异常值和噪声敏感，因为定义一个合适的相似性度量必须考虑所有时间点，包括时间序列数据噪声本身、不同的序列长度、不同的动态、不同的尺度等，这些都可能影响相似性度量。因此，获得最佳的聚类结果可能需要的不仅仅是一个好的相似性度量。
在基于特征的方法中，将原始时间序列数据转换为低维特征向量，然后选择合适的聚类方法进行聚类。 郭等人。 [32]利用独立成分分析（ICA）方法将原始时间序列转换为低维特征向量，然后将改进的K均值聚类方法应用于提取的特征向量。 林等人。 [20]采用符号聚合近似（SAX）方法将时间序列从预定义的字母表转换为符号序列。 SAX采用滑动窗口的方式进行降维，然后通过松弛时间序列的趋势来实现聚类。 此类方法减轻了噪声或异常值的影响并减少了数据量。 然而，这些方法将时间序列的特征提取视为预处理步骤，在特征提取后对它们进行聚类。 在上述过程中，关于时间序列本身的潜在重要数据特征信息丢失了。 因此，仅使用从传统时间序列方法提取的特征可能不足以进行聚类。
深度学习在计算机视觉领域的兴起为聚类技术带来了显著的进步[33]。深度聚类涉及训练神经网络以学习独特的特征表示，使得数据能够被划分为几个不相交的组，而无需强烈的手动指导。在深度聚类方法中，学习到的数据表示的质量和聚类目标的优化对于实现高性能至关重要。现有方法通常关注特征学习和聚类的联合优化，这涉及到学习数据的表示并使用这些新表示进行聚类任务。例如，Yang等人[34]提出了一种联合降维（DR）和k-means聚类方法，其中DR是通过学习深度神经网络来实现的。通过联合优化堆叠自编码器进行降维和基于KL散度计算的K-means聚类目标，获得了良好的性能。类似地，Caron等人[35]提出了一种聚类方法，用于联合学习神经网络参数和结果特征的聚类分配。首先，使用K-means对潜在空间中训练集进行聚类，以获得每个对象的分配。然后，优化编码器参数以预测这些伪标签。除了高性能之外，DNNs是端到端系统，不需要额外的预处理步骤，从而节省了设计复杂框架的时间。上述聚类方法旨在学习有用的数据表示，同时忽略了数据样本之间的结构信息表示。然而，最近，图卷积网络（GCNs）受到了越来越多的关注。图是描述数据样本之间全局关系的有力机制[36]。Bo等人[37]提出了一种整合自编码器和GCN模块的方法，以考虑图数据的结构和特征信息，从而实现更好的表示学习。尽管图数据的结构信息可以反映数据之间的全局关系，但最新的深度聚类方法是为了静态数据而设计的，不适用于时间序列数据聚类。原因是这些方法提取的特征是线性的，而时间序列往往是非线性的。

3.方法

在本节中，我们正式定义问题，然后介绍我们提出的时间序列深度图聚类方法。 本研究的研究框架如图1所示。该框架包括图数据构建和深度图聚类的过程。 表1列出了本文中使用的数学符号。在下面的部分中，我们将对此进行详细说明。

3.1 问题定义

......我们基于X构建图数据，用于序列间相似性度量，以帮助执行深度图聚类方法。每个簇Si由多个形状相似的时间序列表示，这些时间序列描述了动画系列在在线天数维度上观看次数的整体演变模式。解决上述问题使我们能够发现TSAVC演变中的相似模式......

3.2 提出方法

3.2.1. 图数据构建阶段

如果不降低影响，相似性度量可以用来捕捉时间序列内部的局部关系，并将TS-AVC数据转换为G-AVC数据。也就是说，我们首先使用序列间相似性度量构建一个包含n个序列节点的图，然后在这个图中为每个节点选择最近的k个邻居节点来构建图数据。每个时间序列由一个节点表示，使用距离函数度量在节点之间构建边，形成图数据。这个阶段不仅揭示了将时间序列数据从时间-空间域转换为拓扑域中的图数据的过程，而且构建的图数据可以捕捉时间序列数据的全局关系，以减少数据量并提高聚类效率。
时间序列聚类在很大程度上依赖于合适的相似性度量；相似性度量的质量直接影响最终的聚类性能[38]。具体来说，时间序列之间的距离大小决定了序列之间的相似度，距离越小意味着相似度越高。因此，本研究使用距离度量来确定时间序列的相似性，并有可能捕捉到更多的不变性，因为距离度量考虑了序列上的所有时间点。此外，时间序列之间的距离也代表了图数据中边的距离；边的距离大小影响图数据的构建。同时，在深度图聚类阶段的数据包括构建的图数据和原始时间序列数据。因此，合适的序列间相似性度量有助于构建高质量的图数据，并为深度图聚类提供部分数据支持。
对于 x = {x1, x2,…, xt} 和 y = { y1, y2,…, yt } ，如果在所有时间点定义了两个时间距离之间的距离，则 dist(x, y) 是 点之间的距离，如方程(1)所示。

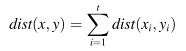
在本文中，我们参考了 Javed 等人[39]关于时间序列相似性度量并使用以下三个时间序列距离来度量相似性。
（1）欧氏距离：测量两个长度相等的时间序列[15]

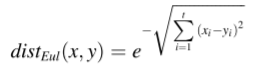
（2）DTW：对于x和y，构造任意两点之间距离的n×m距离矩阵M，其中d(i, j)表示时间序列数据点xi和yj之间的距离，即d(i, j) = (xi − yj)2。 DTW的基本思想是从距离矩阵中得到一条曲线路径W={w1,w2,…,wH}，使两个序列之间的累积距离最小。DTW(x, y) = γ(n,m)



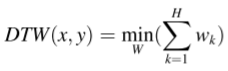
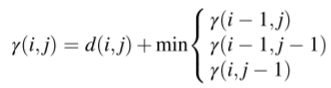
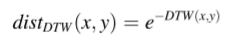
DTW算法：

（3）SBD：SBD是一种基于互相关计算的距离方法。 该方法通过有效的计算推导出具有恒定尺度和恒定位移的时间序列的相似性测度。 对于 x 和 y，使用方程式 6 计算两个序列的相似度：其中CCs(x, y)是长度为2t−1的互相关序列，其结构如图2所示。s ∈ {1,2,⋯,2t−1}。



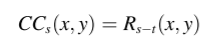
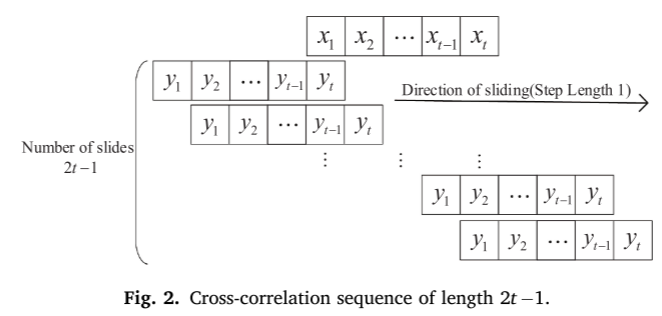
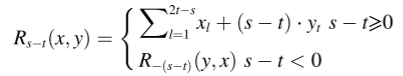
如果互相关系数没有标准化，那么来自多个时间序列成对比较的互相关序列将会出现振幅差异，因为影响互相关序列的因素是时间序列数据本身的大小。互相关系数的标准化有两个优点。一方面，它可以消除相关序列的振幅差异，以显示它们是对齐的。另一方面，它不需要移动，更好地反映了两个时间序列在移动过程中形状的相似性。标准化互相关系数（NCCs）的值在-1和1之间[17]。互相关序列系数的值越大，表示两个序列之间的正相关性越高。具体细节见(8),其中R0为两个相似序列之间不发生相对位移时的互相关系数。


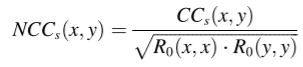
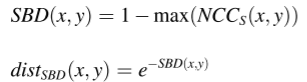
SBD值的范围是0到2。SBD越小，两条曲线越相似。 SBD 相似性度量的完整算法如表 3 所示。

我们使用 Xn×t 中的每一行来计算与所有其他行的相似度值，最终得到欧氏距离/DTW/SBD的相似度矩阵Sn*n。
具有n个时间序列节点的图可以用邻接矩阵A[40]表示。 我们通过选择相似性矩阵 Sn×n 的每行中最近的 k 个元素并将其余元素分配为 1 或 0 来构造邻接矩阵 An×n。在这项研究中，我们选择了k = {5, 10, 15, 20}用于图构建，并将它们最终输入到深度图聚类网络中进行训练，以获得最优节点图的聚类效果。

3.2.2 深度图聚类阶段

深度图聚类的核心思想是学习到的高质量特征有助于提高聚类方法的性能，而聚类结果又可以指导神经网络学习更好的特征。 该过程由三个模块组成：TCN-AE、GCN 和双重自监督。 为了更好地执行聚类任务，TCN-AE和GCN模块分别学习原始时间序列数据的特征信息和图数据的结构信息。 双自监督模块将上述两个模块结合起来，完成网络自监督训练。
（1）TCN-AE
自动编码器（AE）是最常用的以无监督方式训练的神经网络，也是最早、最广泛用于聚类任务的网络。 它通常由两个子网络组成：编码器和解码器。 在本研究中，AE还被用来学习原始时间序列数据的特征。 我们使用 TCN 作为 AE 的构建块。 TCN主要由堆叠的一维全连接卷积层组成，每个基本卷积层都包含因果卷积。 TCN 实现了因果卷积，它在每一层中使用过去和当前的信息来实现更好的时间建模。 TCN还强调通过结合更深的网络深度和扩展卷积来提高时间序列特征的学习能力。 最近的研究表明，TCN 的时间序列建模效果优于 LSTM 模型 [41]。
TCN-AE 模块由编码器网络 Eec(⋅) 和解码器网络 Dec(⋅) 组成。 图 3 左侧所示的编码器 Eec(⋅) 尝试生成一个紧凑的表示，以捕获输入序列的主要特征，并允许在后续步骤中进行相当好的重建。 编码器由 L 层组成，用 E(l) ∈ RFl×Tl 表示，其中 Fl 是第 l 层中卷积滤波器的数量，Tl 是相应的时间步数。 前l层由时间卷积和非线性激活函数组成，最后一层由最大池化层组成。

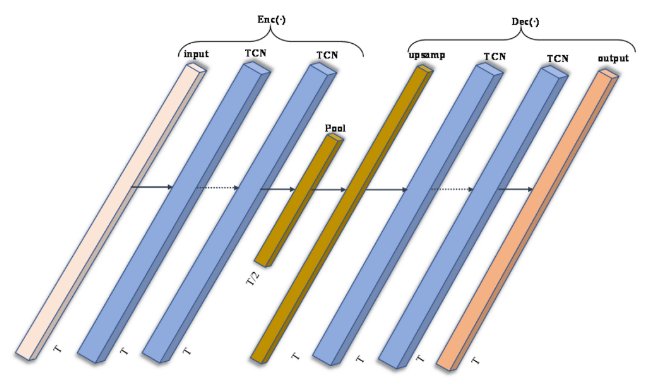
图3：TCN-AE模块由Encoder和Decoder组成； 编码器由时间卷积层和池化层组成，解码器由上采样层和时间卷积层组成。
具体来说，TCN网络在Encoder中第l层学习到的表示为E(l)：编码器中的最后一层 L 是池化层


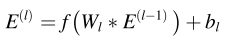
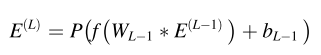
f(.)是激活函数，这里使用Relu激活函数。
上采样：通过简单地重复每个条目两次来恢复原始序列的长度来执行。
重构损失：

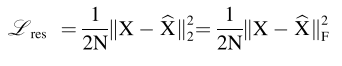
（2）GCN模块
在这项研究中，我们使用图卷积网络（GCN）模块来学习从时间序列转换而来的图数据，使用图的邻接矩阵和节点的特征矩阵作为输入，并不断聚合节点的邻居信息，从而将节点之间的关系信息整合到节点的嵌入特征学习中。同时，该过程还整合了TCN-AE模块学习的时间序列数据的特征信息，使得GCN模块能够学习两种不同类型的信息，包括图数据的结构信息和时间序列数据的特征信息。具体来说，第l层GCN学习了Z(l)的表示。f(.)是relu激活函数。

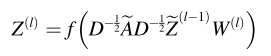
以下同SDCN，其中ε为平衡系数，统一取0.5。

GCN 的最后一层是使用 softmax 函数的多分类层。 概率分布如方程(21)所示。

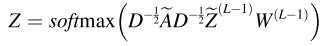
(3)双自监督模块
使用TCN-AE和GCN模块，我们的模型获得了原始时间序列数据的特征表示和图数据的结构表示。然而，这些表示中的大多数并不一定适合聚类，因为它们不输出一个离散的潜在空间，尽管它们很好地描述了输入时间序列的信息。在这种情况下，很难区分每个簇。为此，我们参考了Bo等人[37]提出的使用双重自监督模块来优化聚类结果分布的想法。该模块将TCN-AE和GCN模块集成到一个统一的模块中，以实现模型的端到端自监督训练。我们使用学生t分布来计算自编码网络特征的类别分布，使用softmax函数来获得图神经网络特征的类别分布，并使用KL散度[42]来约束上述两个类别分布与目标分布之间的相似性。
时间序列聚类的规则如下。 首先，对于第 i 个样本和第 j 个聚类，我们使用 Student-t 分布作为核来测量时间编码器的隐藏层表示 ei 与聚类中心 μj 之间的相似度。 qij 可以认为是样本 i 被分配到簇 j 的概率，属于软分配。 将 Q 视为簇分配分布，其计算公式如下：其中 ei 是编码器隐藏层 E(L) 的第 i 行，μj 是在自编码器学习到的预训练表示上使用 K 均值初始化的簇中心，ϑ 是学生的自由度 t 分布：

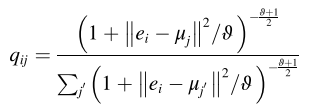
其次，在获得聚类分配分布Q之后，目标分布P必须从高置信度分布中学习聚类友好的表示。 也就是说，表示应该靠近集群中心以提高集群内的凝聚力。

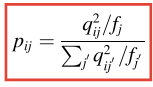
第三，为了使时间自编码网络的聚类分配分布Q更接近目标分布P，我们使用KL散度作为聚类优化的目标函数。



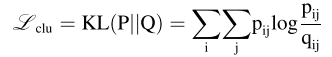
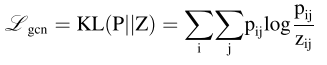
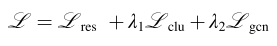
第五，训练结束后，根据Z的结果，我们将每个样本点的聚类标签Ri等同于Z分布中概率最高的类。 因为GCN学习的表示包含两种不同的信息。

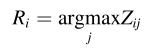
4 实验

4.2 数据预处理

（1）首先，填充缺失值。 每行缺失值均用上下数据填充，保证时间序列数据的数值连续性。
（2）其次，我们进行异常值剔除。 我们将异常值定义为该剧出现次数序列中的数据为0。由于该动画系列可以被关注者观看，因此爬虫的数据必须剥离不完整的数据值。 例如0出现的次数较多，可能是网站更新错误造成的，所以可以去掉该顺序。
（3）第三，我们进行数据标准化。 为了避免由于样本中时间序列数据的数量级差异较大而导致聚类性能下降，我们使用z-score归一化对TS-AVC数据进行归一化，将其转换为0到1之间的数据。

4.3 baseline

K-means是使用欧氏距离比较相似度后对时间序列数据进行聚类[30]。 K-shape在使用归一化互相关度量后进行聚类[17]。 这两种方法代表了传统的浅层聚类方法。 DTC 使用顺序自编码器来学习时间数据的表示，并使用时间聚类层对表示进行聚类[21]。 DTCR使用序列自编码器来学习时间序列数据的隐藏层向量表示，并添加伪样本鉴别器和软K均值来增强聚类效果[22]。 SDCN使用GCN和DNN自编码器联合构建一个将结构信息集成到深度聚类中的网络[37]。 这三种方法代表了深度聚类方法。

4.4 评价指标

4.5 参数设置

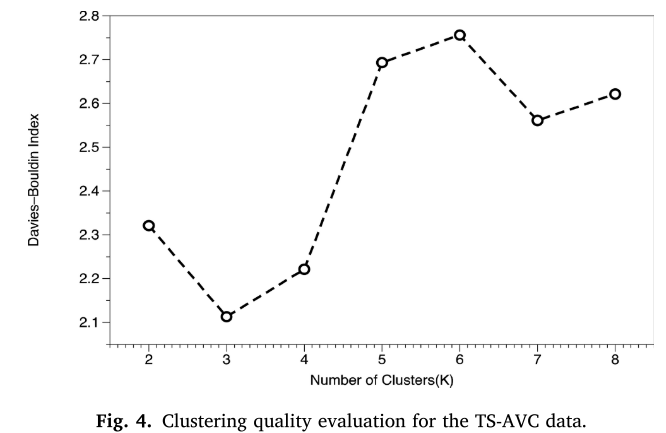
在运行TDGC算法之前，必须设置以下初始条件：通过与内部指标Davies-Bouldin Index比较确定，动画序列数据集的最佳聚类数为K = 3。由于两个时间序列数据集的规模相对较小，我们使用了三个膨胀卷积层，膨胀率分别为r = (0, 0, 1)（编码器）和r = (1, 0, 0)（解码器）。在GCN模块中，图卷积层的数量为四层，每层的维度设置为d−200–500-1000–5，其中d是输入数据的维度。为了更好地更新参数，批量大小设置为64，并使用学习率为0.0001的Adam [80]优化器，随着训练的进行，学习率会动态向下调整。训练迭代次数的默认设置为500。我们将损失函数的权重统一设置为λ1 = 0.1和λ2 = 0.01。在实验中，平衡系数ε设置为0.5。此外，我们将相似性度量设置为SBD，并将每个节点的最近邻居数k设置为10。对于DTC、DTCR和SDCN，方法的参数根据原始设置进行设置。【这里的batchsize指的是预训练AE的时候么？】

5 结果与分析

5.1 K值：TS-AVC数据，没有进行过预先聚类，属于是簇数未知的数据集

基于图 4 所示的 DaviesBouldin 指数，K = 3 被定义为对动画系列视频视图的时间序列进行聚类的最佳聚类数。

5.2 对比实验

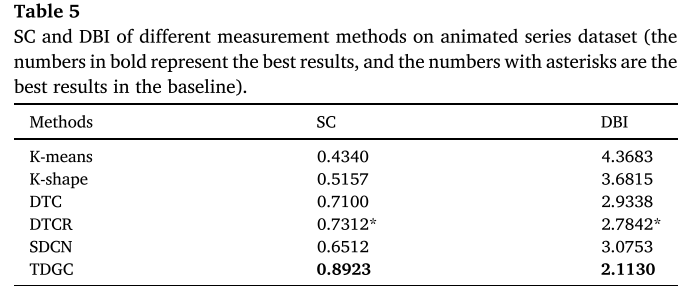
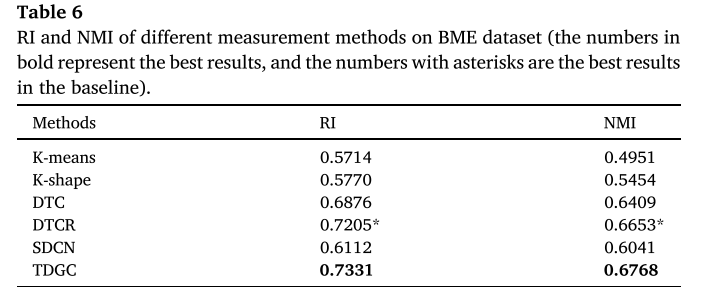
分析：
具体来说，K-means和K-shape的聚类效果相对最差，因为它们直接对原始时间序列数据进行聚类分析，严重依赖序列之间的相似性度量。 其中，K-means使用欧几里德相似性度量，K-shape使用归一化互相关度量。 可以看出，单独考虑时间序列中的相似性测度后的聚类方法不足以获得最佳的聚类结果。 尽管SDCN考虑了原始数据的结构信息，但它并不是仅针对时间序列数据的聚类模型。 它采用DNN网络来学习多类数据的特征表示，导致模型对于时间序列数据的聚类性能相对较差。 与 SDCN 不同，DTC 和 DTCR 是针对时间序列数据提出的两种聚类模型。 DTCR的聚类效果优于DTC。 这是因为虽然DTC和DTCR都依赖于时间编码器的能力来学习表示，但DTC主要使用Bi-LSTM来学习时间数据的表示，而DTCR主要使用双向RNN来学习表示 时间数据并添加伪样本生成策略和辅助分类任务以增强编码器的能力。 同时，它们仅利用原始时间序列内的特征信息，很少考虑数据之间的结构信息，这没有充分利用数据中的丰富信息，导致聚类性能次优。相比之下，TDGC成功地利用了TCN-AE模块和GCN模块来分别高效学习时间序列数据的特征信息和结构信息，以提高聚类性能。此外，我们选择了合适的SBD相似性度量来构建高质量的图数据，这也有助于TDGC高效聚类。在BME数据集上，我们方法的聚类性能优于具有最佳基线聚类效果的DTCR。然而，两者之间的差异有限。原因是我们的方法主要是针对由动画系列的观看次数形成的波动性时间序列数据提出的。如果使用预训练特征获得的聚类准确度较低，那么在KL散度损失微调后，准确度也无法显著提高。此外，目标分布是从学生t分布计算得出的，其更新频率被用作算法的超参数，这可能对不同的数据集有影响。

5.3 敏感性分析：相似性度量和图数据中邻居节点的数量

由于动画系列内部和之间的观看计数数据存在显着差异，因此考虑动画系列的观看计数数据的本地和全局关系非常重要。 巧妙的是，相似性度量可以洞察数据内的局部关系，也是对深度图聚类性能产生间接影响的标准。这是因为选择合适的相似性度量不仅可以减少异常值和噪声的影响，而且可以为深度图聚类阶段提供高质量的图数据，以辅助高效聚类。 此外，图数据中邻居节点的数量可以洞察数据之间的全局关系，也是图数据构建中的重要参数。 原因是图数据是深度图聚类阶段GCN模块的输入。 它的好坏直接影响GCN模块的特征学习能力，间接影响最终的聚类性能。

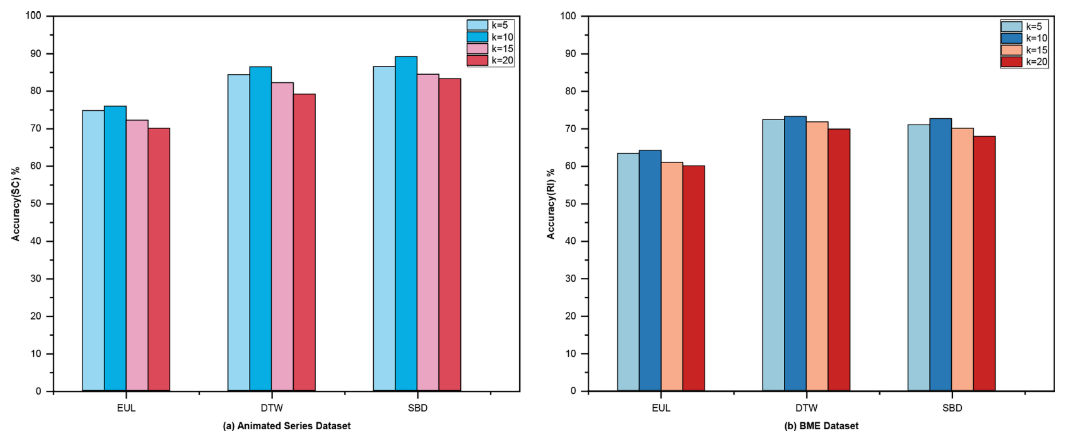
具体分析略
SBD 相似性度量是一种标准化互相关度量，在比较时间序列时考虑时间序列的整体形状。 同时，SBD相似性度量对时间序列数据的幅度和偏移缺乏敏感性，可以有效消除曲线间相位偏差的影响。
对于k = 15和k = 20构建的图数据，节点周围的拓扑结构信息的范围更大，图神经网络可能不太容易学习节点周围的全面结构信息。
因此，对于TDGC方法聚类，选择SBD相似性度量与邻居节点数k=10的图数据的这种组合进行聚类是最优的。

5.4 时间复杂度分析

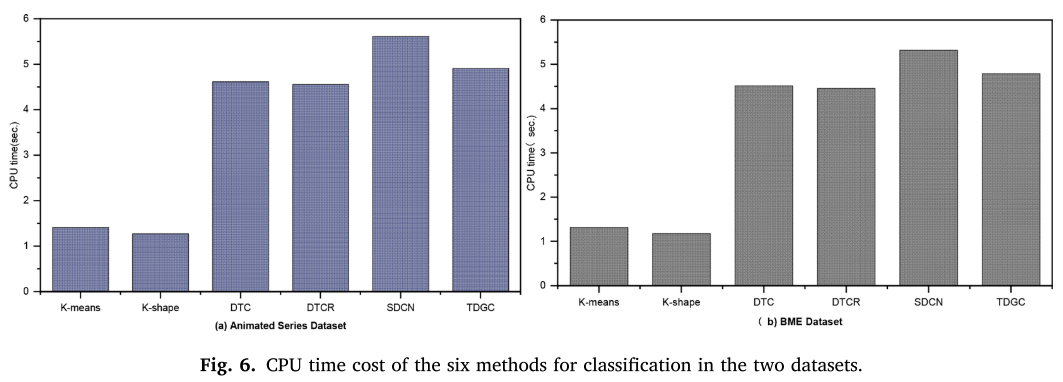
我们提出的 TDGC 方法的运行时间与 DTC 和 DTCR 相当，但比 SDCN 更快。 这是因为选择SBD相似性度量和邻居节点数k = 10的图数据的这种组合有利于时间序列的有效聚类。
同时，应该分析两个最关键的参数，即相似性度量和图数据中邻居节点的数量，以了解它们对我们提出的 TDGC 方法的效率的影响。

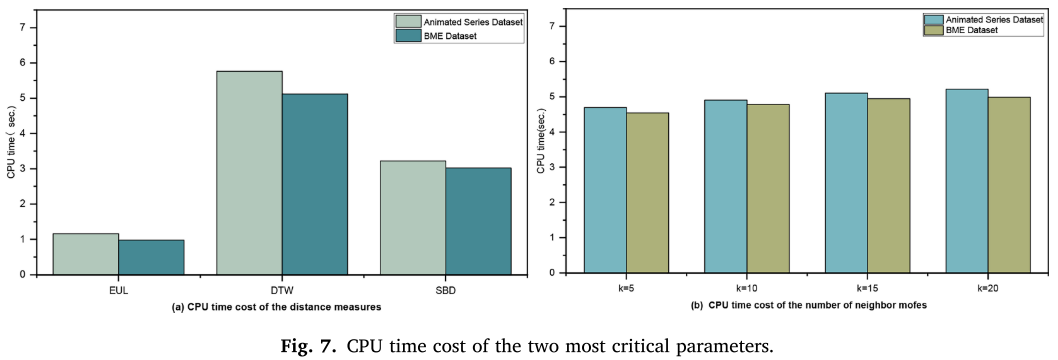
在图 7(a) 中，两个数据集的结果表明，SBD 测量的运行速度仅比 EUL 测量慢约三倍，但仍然比 DTW 测量快一个数量级。 原因是DTW算法在执行过程中，每一步搜索路径都需要计算上下边界，导致计算成本较大。 严格来说，SBD算法只需要计算两个时间序列之间的形状距离，涉及的参数较少。 因此，SBD相似性度量可以帮助我们提出的TDGC方法改善聚类时间。 图7（b）显示，四种图数据构建方法的运行时间在两个数据集之间没有显着差异，但执行时间随着邻居节点数量的增加而增加。 这是因为当邻居节点数量较少时，图数据包含的结构信息较少，而当邻居节点数量较多时，图数据的结构信息更丰富，并且相对耗时。 因此，在四种图节点构造方法几乎不影响运行时间成本的前提下，我们选择聚类精度较高的邻居节点数k = 10。

5.5 可视化：主要是对动漫数据以及在消费者的角度

5.6 讨论

时间序列聚类方法通常从两个研究角度进行探索。 从时间序列数据的角度来看，大多数方法只考虑数据内的局部关系[16]，而忽略数据之间的全局关系。 从聚类方法本身的角度来看，大多数方法仅考虑单个相似性度量或单个特征表示。 此外，单个相似性度量通常对异常值和噪声敏感，而单个特征表示也可能严重依赖编码器的表示能力。
更重要的是，我们从一个新的角度深入研究了时间序列聚类方法，它融合了时间序列数据的特点和神经网络特征表示的优点。 具体来说，首先，针对动画剧集数据内和数据间差异的特点，既要考虑数据内部的局部关系，又要考虑数据之间的全局关系。 其次，聚类方法的本质是发现整体样本中具有相似特征的数据，并将其分组为一个簇。
适当地，深度聚类中的不同神经网络模块可以高效地学习不同数据类型的特征，而丰富的特征学习更有利于对相似属性进行聚类。 面对时间序列数据和图数据，TCN和GCN分别具有较强的特征表示能力。 因此，同时考虑时间序列数据的关系和神经网络的特征表示能力的重要性怎么强调也不为过。
总之，本研究的研究意义概括为三个方面。 首先，两个过程的巧妙结合，适当的相似性度量和有效的特征表示，可以提高聚类精度。 换句话说，可以通过增加聚类过程中的级数来提高聚类精度。 这一发现与 Guijo-Rubio 等人的观点一致。 [49]并验证了他们的观点。 其次，相似性度量对聚类算法的质量起着重要作用。 同时，没有单一的相似性度量可以在所有数据集上产生最佳结果； 相反，它取决于时间序列本身的形状特征。 最后，有效洞察时间序列数据的关系并通过不同的神经网络学习数据的特征对于提高聚类效果极为有帮助。 此外，我们的研究证实深度聚类在时间序列聚类方面优于传统聚类方法。

首先，所提出的方法关注动画系列视频观看次数的时间序列数据，并在公共数据集上进行简单的扩展实验。 在未来的工作中，我们的方法的通用性将在许多公共时间序列数据集上得到验证。 其次，我们的方法仅考虑单变量时间序列。 然而，同样的想法可以扩展到多元时间序列聚类，至少可以通过以下方式。 一方面，我们可以改变第一阶段时间序列的相似性度量。 在这种情况下，我们只需要使用为多元时间序列设计的新距离函数[50]，而深度图聚类过程的第二阶段保持不变。 另一方面，在第二阶段的深度图聚类模块中，可以为时序数据找到更适合学习数据的深度神经网络，不断优化特征，实现高效聚类。 在我们未来的工作中，我们计划解决这个问题。