2022.10.27

xingke233 / 2024-11-09 / 原文

CSP-S寄了，被 COVID-19 定点打击。

练习情况

P1402 酒店之王

P1231 教辅的组成

P2891 [USACO07OPEN]Dining G

最大流，关键在建图，以 P1402 为例。

一开始我是这样建的。

源点 -> 房间 -> 客人 -> 菜品 -> 汇点

看起来没有问题，但实际上这有很大问题。

如：

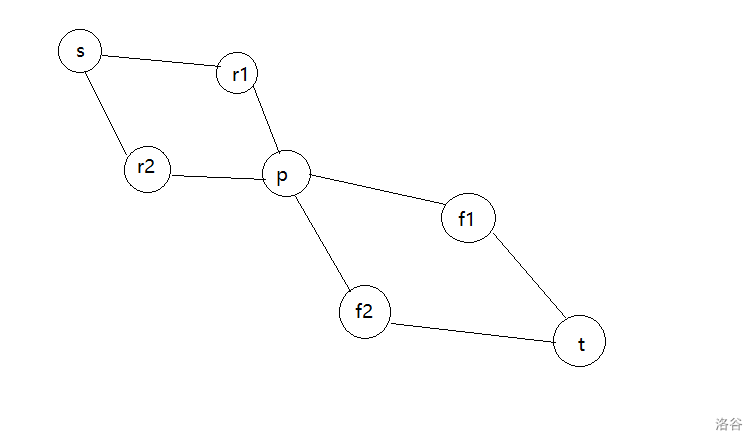
这样的图，一个人就贡献了 2 次。

所以我们将人拆成入点与出点。

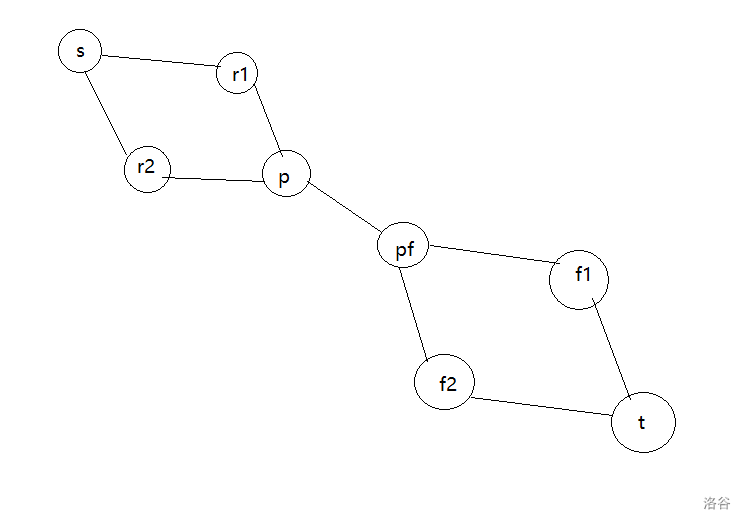
Code:

P1402

P3455 [POI2007]ZAP-Queries

莫比乌斯反演入门第一题。

求： $\displaystyle\sum\limits_{i=1}^a\sum\limits_{j=1}^b[\gcd(i,j)=d]$

开始推柿子。

我们设 $a\le b$ 。

$\displaystyle\sum\limits_{i=1}^a\sum\limits_{j=1}^b[\gcd(\frac{i}{d},\frac{j}{d})=1]$

$\displaystyle\sum\limits_{i=1}^{\left\lfloor\frac{a}{d}\right\rfloor}\sum\limits_{j=1}^{\left\lfloor\frac{b}{d}\right\rfloor}[\gcd(i,j)=1]$

运用反演 $\ \ \displaystyle[\gcd(i,j)=1]=\sum\limits_{d\mid\gcd(i,j)}\mu(d)$

$\displaystyle\sum\limits_{i=1}^{\left\lfloor\frac{a}{d}\right\rfloor}\sum\limits_{j=1}^{\left\lfloor\frac{b}{d}\right\rfloor}\sum\limits_{k\mid\gcd(i,j)}\mu(k)$

枚举 $k$ 得

$\displaystyle\sum\limits_{k=1}^{\left\lfloor\frac{a}{d}\right\rfloor}\mu(k) * \left\lfloor\frac{a}{dk}\right\rfloor * \left\lfloor\frac{b}{dk}\right\rfloor$

后面一坨可以用数论分块降低复杂度。

Code:

#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define Ld long double
const int N = 50005,M=1000005;

LL t,a,b,d,prime[N],vis[N],cnt,mu[N],sum[N];

void mobius(LL n){
    mu[1]=1;
    for(LL i=2;i<=n;i++){
        if(!vis[i]) prime[++cnt]=i,mu[i]=-1;
        for(int j=1;prime[j]<=n/i;j++){
            vis[prime[j]*i]=1;
            if(i%prime[j]==0){
                break;
            }
            mu[i*prime[j]]=-mu[i];
        }
    }
    for(int i=1;i<=n;i++){
        sum[i]=sum[i-1]+mu[i];
    }
    return ;
}

int main(){
    t=read();
    mobius(N-5);
    while(t--){
        a=read(),b=read(),d=read();
        LL ans=0;
        a/=d,b/=d;
        if(a>b) swap(a,b);
        for(LL l=1,r;l<=a;l=r+1){
            r=min(a/(a/l),b/(b/l));
            ans+=(a/l)*(b/l)*(sum[r]-sum[l-1]);
        }
        print(ans);
    }
    return 0;
}