理解共轭函数

她说，她是仙，她不是神 / 2023-09-06 / 原文

以下摘自 https://zhuanlan.zhihu.com/p/642693808

考虑一个可微函数 $f: \mathbb{R}^{n} \rightarrow \mathbb{R}, \operatorname{dom} f=\mathbb{R}^{n}$
对某一点 $\left(x_{0}, f\left(x_{0}\right)\right)$ 作其切线 $l: y=\nabla f(x_0)\left(x-x_{0}\right)+f\left(x_{0}\right)$
当 $x=0$ 时, 得到该切线交轴上的截距 $D=f\left(x_{0}\right)-\nabla f\left(x_{0}\right) \cdot x_{0}$
先放到一边, 对比一个函数 $f^{*}(y)=y^{T} x-f(x)$
可以发现, 对任意一个给定的点 $\left(x_{0}, f\left(x_{0}\right)\right), x_0 \in \operatorname{dom} f$, 当 $y=\nabla f\left(x_{0}\right)$ 时, $f^{*}(y)$ 的值
为该点在函数 $f(x)$ 上对应切线的截距的相反数, 即 $f^{*}(y)=\nabla f\left(x_{0}\right) \cdot x_{0}-f\left(x_{0}\right)=-D$
现在再来看看共轭函数, $f(x)$ 的共轭函数 $f^{*}(y)=\underset{x \in dom f}{\sup }\left(y^{T} x-f(x)\right)$
首先根据定义, $y^{T} x-f(x)$ 是关于 $y$ 的一个凸函数（因为 $y^{T} x$ 是对 $y$ 的线性变换）, 取凸函
数的逐点上确界是保凸运算, 所以共轭函数一定是凸函数。
对于任意给定的一个自变量值 $y=y_{0}$, 等式右边的意思是, 作一条梯度为 $y_{0}$ 且过原点的直线
$y_{0}^{T} x$, 取遍 $d o m f$ 中的点 $x$, 它与 $f(x)$ 相减的最大值。
不难发现, 若 $f$ 可微, 当某点 $\left(x_{0}, f\left(x_{0}\right)\right)$ 使得 $y_{0}=\nabla f\left(x_{0}\right)$ 时, $y^{T} x-f(x)$ 的值最大。
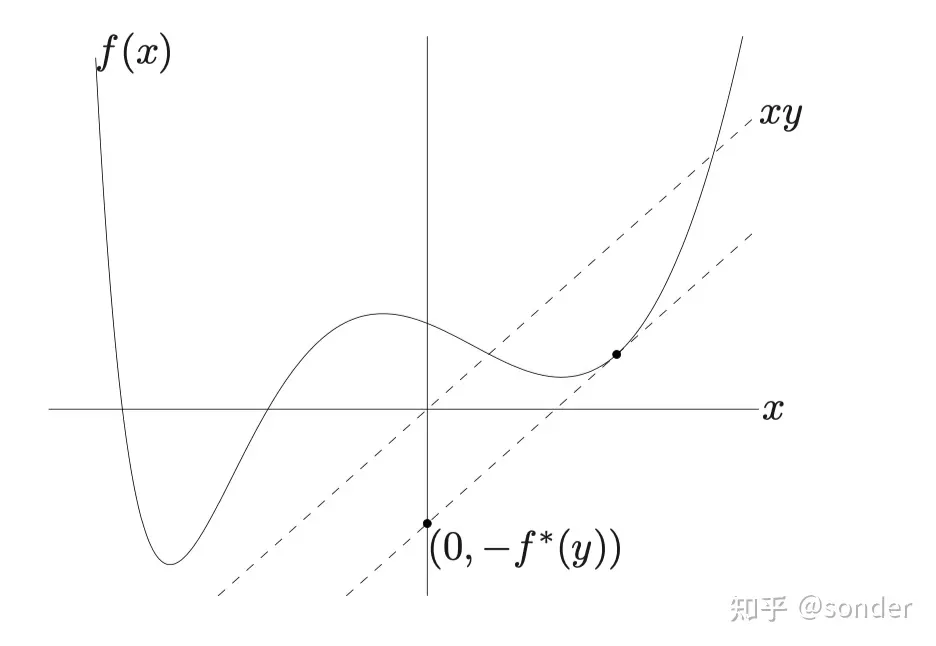
例如, 若 $f$ 是 $\mathbb{R} \rightarrow \mathbb{R}$ 的一个映射, $y_{0}^{T} x-f(x)$ 相当于直线 $y_{0} x$ 与函数的差值。可以发现,
对于某点 $\left(x_{0}, f\left(x_{0}\right)\right)$, 其切线的斜率恰好等于 $y_{0}$ 时, 两直线间距离最大, 也就是对于这两条平
行线, 截距之差最大。

以下摘自 https://zhuanlan.zhihu.com/p/400597409

一个函数 $f: R^{n} \rightarrow R$，其共轭函数(conjugate function) 定义为
$f^{*}(y)=\sup _{x \in \operatorname{dom} f}\left(y^{T} x-f(x)\right)$
使上述上确界有限, 即差值 $y^{T} x-f(x)$ 在 $d o m f$ 有上界的所有y 构成了共轭函数的定义域。
共轭函数 $f^{*}(y)$ 是线性函数 $y^{T} x$ 和 $f(x)$ 之间的最大差值，如果f可微，则在满足 $\nabla f(x)=y$ 的
点x处差值最大。
显而易见, $f^{*}(y)$ 是凸函数，因为它是一系列 $y$ 的凸函数（实质上是仿射函数）的逐点上确界。
无论 $f$ 是否为凸函数， $f^{*}$ 都是凸函数。

常见凸函数共轭函数

凸二次函数 $f(x)=(1 / 2) x^{T} Q x, Q \in \mathbf{S}_{++}^{n}$
$\begin{aligned} f^*(y) & =\sup_{x} \left(y^{T} x-(1 / 2) x^{T} Q x\right) \\ & =\frac{1}{2} y^{T} Q^{-1} y\end{aligned}$
范数平方 $f(x)=(1 / 2)\|x\|^{2}$
$f^{*}(y)=(1 / 2)\|y\|_{\star}^{2}$
范数 $f(x)=\|x\|$
$f^*(y)=\left\{\begin{array}{ll}0 & \|y\| \leq 1 \\ \infty & \text { otherwise }\end{array}\right.$
- 对于绝对值函数，可以从几何上理解。对于一般$p$范数，严格证明如下？
- https://mathworld.wolfram.com/HoeldersInequalities.html
  - Hoelders不等式证明 https://zhuanlan.zhihu.com/p/114469435
  - 基于Cauchy-Schwarz不等式推广 https://image.hanspub.org/Html/10-1251477_48972.htm
- 参考 https://zhuanlan.zhihu.com/p/435757883