高级算法指北——李超线段树及其应用
I 走进李超线段树
定义
李超线段树是一种用于维护多条一次函数的线段树。你可以使用它在 \(O(\log n)\) 的复杂度内插入一条新的直线,或是查询所有直线 \(y=k_ix+b_i\) 中,当 \(x=x_0\) 时,\(y\) 的最值。
李超线段树上的每个节点都维护当前区间的中点处,\(y\) 的最值。
修改操作
有一个很显然的修改方式——每插入一条直线,就到最底端的节点修改。这样的时间复杂度显然错误,且我们并没有把所有的节点都利用起来维护信息。
以维护最小值为例,考虑下面一种情况。点 \(x\) 是线段树上的一个节点,\(mid\) 是 \(x\) 所代表的区间的中点。原来,使 \(y\) 取到最大值的直线编号是 \(t_x\),现在新增的直线编号是 \(p\)。不难发现,新增一条直线 \(p\) 后,该点的答案直线会更新,且仅有左区间中的答案不确定,右区间的答案一定与该点的答案相同。为了使修改做到 \(O(\log n)\),我们不再遍历与父亲区间答案相同的区间,而只遍历有可能答案不同的区间。这样一来,每一次都只会修改左右区间中的 \(1\) 个,时间复杂度就正确了。我们把这种对 区间修改、单点查询 起效的方法称作“标记永久化”。
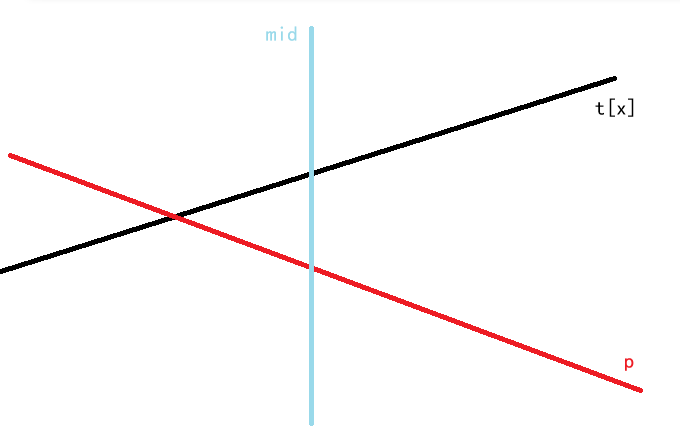
我们可以依照 \(x\) 点处的新答案是谁,和斜率的大小关系分类讨论,并在可能更改答案的区间继续遍历。通过画图很容易判断出可能更改答案的区间是哪一个。下面给出维护最小值的情况下修改的函数。
inline int gety(int id,int x){//这是求函数值的
if(id==0)return inf;
return k[id]*x+b[id];
}
void modify(int x,int le,int ri,int p){
//这里的p是与父亲节点答案不同的、可能成为该区间答案的直线标号,并不一定是新加入进来的直线编号。
if(le==ri){
if(gety(p,le)<gety(t[x],le))t[x]=p;
return;
}
int mid=(le+ri)>>1;
if(gety(t[x],mid)>gety(p,mid)){//p的直线在 mid 处更优,答案就调成 p,t[x]下方看后面有没有t[x]更优的。
if(k[p]>k[t[x]])modify(rs(x),mid+1,ri,t[x]);
else modify(ls(x),le,mid,t[x]);
t[x]=p;//标记永久化
}
else{
if(k[t[x]]>k[p])modify(rs(x),mid+1,ri,p);
else modify(ls(x),le,mid,p);
}
}
查询操作
单点查询,时间复杂度显然正确。需要注意的是由于 标记永久化 的存在,路径上遇到的任意一个答案都可能是最终的答案,而叶子节点处可能根本没有记录答案。所以需要将路径上遇到的所有答案取最值作为最终结果。
如上图中右区间的任意一个点的答案都在 \(x\) 节点处被记录,而没有继续往下传递。所以需要在 \(x\) 处求出答案并和其它可能答案取 \(\min\)。
下面给出查询的函数。
int query(int x,int le,int ri,int p){//这里的p是横坐标
if(le==ri)return gety(t[x],p);
int res=gety(t[x],p);
int mid=(le+ri)>>1;
if(p<=mid)return min(res,query(ls(x),le,mid,p));
else return min(res,query(rs(x),mid+1,ri,p));
}
经典例题
[JSOI2008] Blue Mary 开公司
显然,每一个 Project 都是一个一次函数,每次询问 \(x=T\) 时,哪一条函数的值最大。李超线段树套上去即可。
#include<bits/stdc++.h>
#define ls(x) x*2
#define rs(x) x*2+1
using namespace std;
const int N=1e6+5;
int n,cnt=0;
int t[4*N];
struct func{
double k,b;
}f[4*N];
inline double val(int x,int id){
return f[id].k*(x-1)+f[id].b;
}
void modify(int x,int le,int ri,int id){
if(le==ri){
if(val(le,id)>val(le,t[x]))t[x]=id;
return;
}
int mid=(le+ri)>>1;
if(f[id].k>f[t[x]].k){
if(val(mid,id)>val(mid,t[x])){
modify(ls(x),le,mid,t[x]);
t[x]=id;
}
else modify(rs(x),mid+1,ri,id);
}
else{
if(val(mid,id)>val(mid,t[x])){
modify(rs(x),mid+1,ri,t[x]);
t[x]=id;
}
else modify(ls(x),le,mid,id);
}
}
double query(int x,int le,int ri,int d){
if(le==ri)return val(d,t[x]);
int mid=(le+ri)>>1;
double ans=val(d,t[x]);//标记永久化
if(d<=mid)return max(ans,query(ls(x),le,mid,d));
else return max(ans,query(rs(x),mid+1,ri,d));
}
int main(){
scanf("%d",&n);
while(n--){
char c[10];
cin>>c;
if(c[0]=='P'){
double x,y;
scanf("%lf%lf",&x,&y);
f[++cnt].k=y;
f[cnt].b=x;//原点是第一天
modify(1,1,N,cnt);
}
else{
int x;
scanf("%d",&x);
printf("%d\n",(int)(query(1,1,N,x))/100);
}
}
return 0;
}
II 李超线段树的复杂操作
区间修改
如果我们维护的不是直线,而是只在某个范围内存在的 线段,可以考虑用区间修改的方式找到包含线段的 \(\log n\) 个区间,再从每个区间开始往下执行原来的操作即可。时间复杂度约为 \(O(n\log n)\)。
李超线段树合并
和普通的线段树合并相同,只需要在合并完每个节点后,比较原来的两个节点上的答案,选择最佳的那一个记录即可。复杂度仍然是 \(O(n\log n)\)。
动态开点李超线段树
由于标记永久化的存在,动态开点的李超线段树一次其实只需要新建一个点,新建后即可返回。
int rt[4*N],np,lson[32*M],rson[32*M],t[32*M];
void modify(int &x,int le,int ri,int p){
if(!x){
x=++np,t[x]=p;
return;
}
if(le==ri){
if(gety(p,le)<gety(t[x],le))t[x]=p;
return;
}
int mid=(le+ri)>>1;
if(gety(p,mid)>gety(t[x],mid)){
if(k[p]>=k[t[x]])modify(lson[x],le,mid,p);
else modify(rson[x],mid+1,ri,p);
}
else{
if(k[p]>=k[t[x]])modify(rson[x],mid+1,ri,t[x]);
else modify(lson[x],le,mid,t[x]);
t[x]=p;
}
}
III 李超线段树的应用——优化dp
介绍
对于一类dp,它们的转移形如 \(f_i\leftarrow f_j\),且化简后可以写作 \(y=kx+b\),其中 \(x\) 是含有 \(dp_i\) 一项的式子,\(x\) 是含有与 \(i\) 相关的常量的式子,\(k\) 和 \(b\) 是含有与 \(j\) 相关的值的式子。显然我们可以维护凸包进行斜率优化,但对于 \(x\) 和 \(k\) 不单调的情况,代码难度较高,不容易维护。此时,代码量小的李超线段树是一个很好的选择。
显然,当 \(j\) 转移完毕后,我们可以在李超线段树中加入上文所述的一条直线,并标号为 \(j\)。不难发现 \(dp_i\) 的转移就是在 \(x=x_i\) 时求所有直线中函数值的最值。最基础的李超树即可解决。
经典例题
[CEOI2017] Building Bridges
设 \(dp_i\) 表示建桥连接到第 \(i\) 个柱子时的代价最小值,显然平方拆开后就可以将转移写成一次函数的形式。用李超线段树维护每一个 \(j\) 代表的直线即可。
#include<bits/stdc++.h>
#define int long long
#define rep(i,j,k) for(int i=j;i<=k;i++)
#define repp(i,j,k) for(int i=j;i>=k;i--)
#define ls(x) x*2
#define rs(x) x*2+1
#define mp make_pair
#define fir first
#define sec second
#define pii pair<int,int>
#define lowbit(x) x&-x
using namespace std;
const int N=1e5+5,M=1e6+5,inf=1e18+7;
const double eps=1e-9;
void read(int &p){
int x=0,w=1;
char ch=0;
while(!isdigit(ch)){
if(ch=='-')w=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<1)+(x<<3)+ch-'0';
ch=getchar();
}
p=x*w;
}
int dp[N],h[N],sum[N],k[N],b[N];
int n;
int t[4*M];
inline int gety(int id,int x){
if(id==0)return inf;
return k[id]*x+b[id];
}
void modify(int x,int le,int ri,int p){//这里的p是直线标号
if(le==ri){
if(gety(p,le)<gety(t[x],le))t[x]=p;
return;
}
int mid=(le+ri)>>1;
if(gety(t[x],mid)>gety(p,mid)){
if(k[p]>k[t[x]])modify(rs(x),mid+1,ri,t[x]);
else modify(ls(x),le,mid,t[x]);
t[x]=p;
}
else{
if(k[t[x]]>k[p])modify(rs(x),mid+1,ri,p);
else modify(ls(x),le,mid,p);
}
}
int query(int x,int le,int ri,int p){//这里的p是横坐标
if(le==ri)return gety(t[x],p);
int res=gety(t[x],p);
int mid=(le+ri)>>1;
if(p<=mid)return min(res,query(ls(x),le,mid,p));
else return min(res,query(rs(x),mid+1,ri,p));
}
/*
容易写出dp方程 dpi=dpj+(hi-hj)^2+sum(i-1)-sumj,化简后发现可以斜率优化.由于k和x有不单调,单调队列不容易写,考虑李超树维护.
*/
signed main(){
read(n);
rep(i,1,n)
read(h[i]);
rep(i,1,n)
read(sum[i]),sum[i]+=sum[i-1];
//每一次的李超树都可以从任意一个之前的转移过来,所以直接加全局直线并对 x=hi 单点查询即可.
k[1]=-2*h[1],b[1]=dp[1]+h[1]*h[1]-sum[1];
modify(1,0,1e6,1);
rep(i,2,n){
dp[i]=query(1,0,1e6,h[i])+h[i]*h[i]+sum[i-1];
k[i]=-2*h[i],b[i]=dp[i]+h[i]*h[i]-sum[i];
modify(1,0,1e6,i);
// printf("%lld\n",dp[i]);
}
printf("%lld\n",dp[n]);
return 0;
}
[NOI2014] 购票
容易写出树上 dp 的转移式子并化成一次函数的形式。问题在于可以转移到每个 \(i\) 的直线是不同的。考虑线段树套动态开点李超树,区间在 \([le,ri]\) 的节点套的李超树上仅有标号从 \(le\) 到 \(ri\) 的线段,每一次转移可在 \(\log\) 棵李超树上单点查询并求合起来的最小值。根据前面介绍的动态开点方法,每一条直线只需要在一棵树上新开 \(1\) 个节点,共计开 \(\log\) 个节点,故空间复杂度和时间复杂度均为两只 \(\log\)。
若用树剖维护,会再多一只 \(\log\);若用出栈序边 dfs 边计算答案,可以在两只 \(\log\) 的复杂度内解决问题。
#include<bits/stdc++.h>
#define int long long
#define rep(i,j,k) for(int i=j;i<=k;i++)
#define repp(i,j,k) for(int i=j;i>=k;i--)
#define ls(x) x*2
#define rs(x) x*2+1
#define mp make_pair
#define fir first
#define sec second
#define pii pair<int,int>
#define lowbit(x) x&-x
using namespace std;
const int N=2e5+5,M=1e6+5,inf=1e18+7;
const double eps=1e-9;
void read(int &p){
int x=0,w=1;
char ch=0;
while(!isdigit(ch)){
if(ch=='-')w=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<1)+(x<<3)+ch-'0';
ch=getchar();
}
p=x*w;
}
/*
显然的斜率优化,但不单调,可以用李超线段树维护.考虑到有距离限制,需要查询的是部分线段,改为树套树,每个外层线段树的节点表示该节点
对应的李超树上有哪些线段.由于其非叶子节点上也有标记,李超树上一次新增线段可以只新增1个点,故总的空间复杂度是一只log.
在树上,dfs的过程中要撤销,可以考虑树剖/边dfs,边在出栈序上区间查询。这里用第二种,只带两只log
方程:dpi-di*pi-qi=min(-dj*pi+dpj),每条直线即为y=-dj*x+dpj
*/
int n,tp,nump[N],q[N],l[N],ans[N],dfn[N],id[N],dis[N],fa[N][20];
struct edge{
int to,nxt,v;
}e[2*N];
int fir[N],np;
int k[N],b[N];
int gety(int j,int x){
if(j==0)return inf;
return k[j]*x+b[j];
}
struct lctree{//李超树
int rt[4*N],np,lson[32*M],rson[32*M],t[32*M];
void modify(int &x,int le,int ri,int p){
if(!x){
x=++np,t[x]=p;
return;
}
if(le==ri){
if(gety(p,le)<gety(t[x],le))t[x]=p;
return;
}
int mid=(le+ri)>>1;
if(gety(p,mid)>gety(t[x],mid)){
if(k[p]>=k[t[x]])modify(lson[x],le,mid,p);
else modify(rson[x],mid+1,ri,p);
}
else{
if(k[p]>=k[t[x]])modify(rson[x],mid+1,ri,t[x]);
else modify(lson[x],le,mid,t[x]);
t[x]=p;
}
}
int query(int x,int le,int ri,int p){
if(!x)return inf;
int res=gety(t[x],p);//每个点都记录信息,每个点都要记录贡献
if(le==ri)return res;
int mid=(le+ri)>>1;
if(p<=mid)return min(res,query(lson[x],le,mid,p));
else return min(res,query(rson[x],mid+1,ri,p));
}
}T;
void add(int x,int y,int w){
e[++np]=(edge){y,fir[x],w};
fir[x]=np;
}
int cnt;
void dfs_pre(int x,int f){
fa[x][0]=f;
rep(i,1,19)
fa[x][i]=fa[fa[x][i-1]][i-1];
for(int i=fir[x];i;i=e[i].nxt)
dis[e[i].to]=dis[x]+e[i].v,dfs_pre(e[i].to,x);
dfn[++cnt]=x,id[x]=cnt;
}
int farth(int x){//倍增
int nw=x;
repp(i,19,0){
int j=fa[nw][i];
if(!j)continue;
if(dis[x]-dis[j]<=l[x])nw=j;
}
return nw;
}
void modify(int x,int le,int ri,int p){
T.modify(T.rt[x],0,1e6,p);//每个节点都代表一个包含直线p的李超树,都要建树.
if(le==ri)return;
int mid=(le+ri)>>1;
if(p<=mid)modify(ls(x),le,mid,p);
else modify(rs(x),mid+1,ri,p);
}
int query(int x,int le,int ri,int ql,int qr,int p){
if(ql<=le&&qr>=ri){//返回这一部分线段的答案
int ret=T.query(T.rt[x],0,1e6,nump[dfn[p]]);
return ret;
}
if(!x)return inf;
int mid=(le+ri)>>1;
int ret=inf;
if(ql<=mid)ret=min(ret,query(ls(x),le,mid,ql,qr,p));
if(qr>mid)ret=min(ret,query(rs(x),mid+1,ri,ql,qr,p));
return ret;
}
void dfs_solve(int x){
if(x!=1){
int l=id[fa[x][0]],r=id[farth(x)];//x最远能到达的节点.
ans[x]=query(1,1,n,l,r,id[x])+dis[x]*nump[x]+q[x];//边走边算答案,这样在出栈序中无关的点的李超线段树还没有建立起来.
}
k[id[x]]=-dis[x],b[id[x]]=ans[x];modify(1,1,n,id[x]);//printf("%d %lld %lld\n",x,k[x],b[x]);
for(int i=fir[x];i;i=e[i].nxt)
dfs_solve(e[i].to);
}
signed main(){
read(n),read(tp);
rep(i,2,n){
int x,s;
read(x),read(s),read(nump[i]),read(q[i]),read(l[i]);
add(x,i,s);
}
dfs_pre(1,0);//出栈序
dfs_solve(1);
rep(i,2,n)
printf("%lld\n",ans[i]);
return 0;
}
李超线段树的主要内容到此就结束啦!
QwQ