电路与电子技术基础(1)
电子与电子技术基础初步
电路的组成
-
电源
例如: 蓄电池和干电池: 化学能转换成电能
-
负载
实际的负载包括电动机、电动工具和家用电路
-
导线
-
开关
电路的作用
-
电能的传输、转换
-
信号的传递、处理
电路的基本物理量
大写直流--不变
小写交流--变化
-
电流 \(I\) \(i\)
方向: 正电荷定向移动的方向,高电位流向低电位
-
电压 \(U\) \(u\)
电位降低的方向(高电位 --> 低电位)
-
电动势 \(E\) \(e\)
电源力驱动正电荷的方向(低电位 --> 高电位)
-
功率 \(P\)
用电或供电
电压与电动势
| 基本量 | 性质 |
|---|---|
| 电动势 \({E}\) | 电动势的方向电位升 |
| 电压 \({U}\) | 电压的方向电位降 |
电路中的参考点
-
概念: 在分析和计算电路时,常把电路中的抹一点选作参考点,并规定其电位为零,也称为地
-
符号: 常用"\(\perp\)"表示
-
作用: 电路中各点的电位只有在参考点选定后才有确定的数值 -- 单值性
-
选取方法和原则: 可以任意选择,但一般常选大地或机壳作为参考点; 且在分析电路的过程中一经选定不可随机更改
电路常见解决方法
在解题前先任意选定一个方向,称为参考方向 (或正方向)。依此参考方向,根据各个公式定理进行电路的分析计算
-
根据计算结果确定U, I的实际方向
-
计算结果为正,实际方向与假设方向一致
-
计算结果为负,实际方向与假设方向相反
-
电路中的参考方向
-
电流参考方向
-
电压参考方向
电流和电流方向
-
大小: 单位时间内流过导体横截面积的电荷量(单位:安培 A)
-
普遍定义: \(i = \lim\limits_{\Delta t\to0}{\frac{\Delta q}{\Delta t}}\)
-
交流: \(i = \frac{dq}{dt}\)
-
恒定电流: \(I = \frac{\Delta q}{\Delta t}\)
-
-
方向: 正电荷的宏观运动方向
-
电流可以作为时间函数(常量可以堪称时间函数特例), 电流是代数量,其值可以为正,也可以为负
因为是代数量,所以正负号仅仅只代表方向,如果为正,则与参考方向相同,如果为负,则与参考方向相反
note: 电流中的参考方向可以随意规定,但是一经规定后,在计算过程中不得任意改变
- 参考方向的表示方法
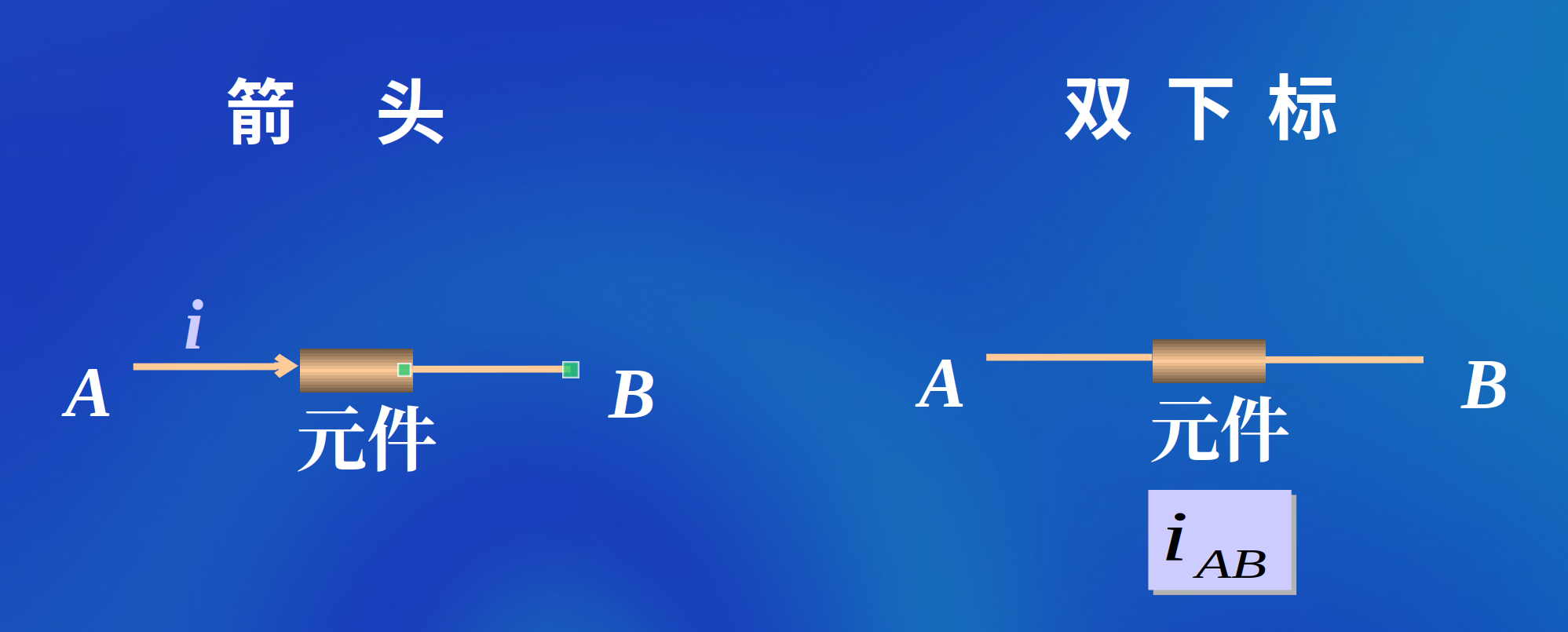
电压的参考方向

| 电压情况 | 实际情况 |
|---|---|
| \(u > 0\) | 实际电位A点高于B点电位 |
| \(u < 0\) | 实际电位B点高于A点电位 |
- 作为时间函数(常量可以堪称时间函数的特例)的电压是代数量,其数值可以正,也可以负。正负仅仅代表方向而已
note: 电压的参考方向可以随意规定,但是一经规定后,在计算过程中不得任意改变
电压参考方向的表示
| 表示方法 | 写法 |
|---|---|
| \(+ -\) |  |
| 双下标 |  |
| 箭头 | 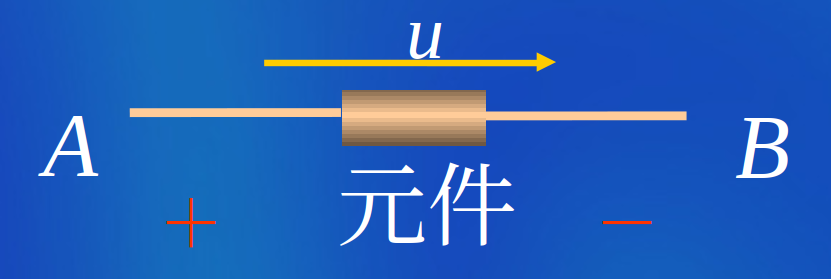 |
关联参考方向
-
定义: 元件电流的参考方向是从标以电压正极性的一端指向负极性一端,即电流和电压的参考方向一致,称为关联参考方向
-
关联性的描述方式
| 情景 | 描述 |
|---|---|
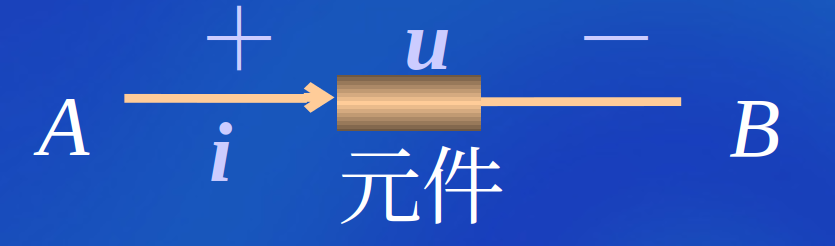 |
参考方向关联 / 参考方向一致 |
 |
参考方向不关联 / 参考方向不一致 |
note:
- 电路计算中,参考方向的选择是任意的,但是一经选定后,解题过程中一般不再变动。
- 电压、电流的真是指向是客观存在的,若设定的参考方向相反,则计算结果的代数符号也会相反。
- 电路分析过程中,必须画图并标定参考方向和回路的绕行方向,否则计算结果无意义。
关联方向在问题解决方面的应用
-
电压电流 "实际方向" 是客观存在的物理现象,"参考方向"是认为假设的方向。
-
\({R} = \frac{{U}}{{I}}\) 只适用于 \({R}\) 中 \({U}\) 、\({I}\) 参考方向一致的情况——欧姆定律表达式含有正负号。
-
在解题前,一定先假定电压电流的“参考方向”,然后再列方程求解。即 U、I为代数量,也有正负之分
-
为方便列电路方程,习惯假设I与U的参考方向一致(关联参考方向)
功率的计算及其意义
- 计算
-
意义
-
若计算结果 \(P > 0\) , 则说明U、I的实际方向一致,此部分电路吸收电功率(消耗能量)即 负载
-
若计算结果 \(P > 0\) , 则说明U、I的实际方向相反,此部分电路输出电功率(提供能量)即 电源
-
-
性质
- 在同一电路中,电源产生的总功率和负载消耗的总功率是平衡的
电气设备的额定值
-
额定电流 \(({I}_{{N}})\):
电气设备在长期连续运行或规定工作制度下允许通过的最大电流。
-
额定电压 \(({U}_{{N}})\):
电气设备根据所用绝缘材料的耐压程度和容许温升等情况,所规定正常工作时的电压。
-
电气设备的额定值:
额定电压、额定电流、额定功率 \({P}_{{N}}\) 以及其他规定值 (电动机的额定转矩等)。
-
常见符号:
符号 意义 \({U}_{{N}}\) 额定电压 \({I}_{{N}}\) 额定电流 \({P}_{{N}}\) 额定功率 \({n}_{{N}}\) 额定转速 --- --- note: N -- normal
-
性质意义:
-
负载设备通常工作与额定状态
-
电源设备的额定功率标志电源的供电能力,是长期运行允许的上限值
-
电源输出的功率由外电路决定,不一定等于电源额定功率
-
电路的三种工作状态
| 电路图 | 状态 | 物理量的关系 | 电路状态 |
|---|---|---|---|
| 开路 |  |
\(I = 0\) \(U_0 = E\) | 开路状态: 开关S打开 |
| 有载 | 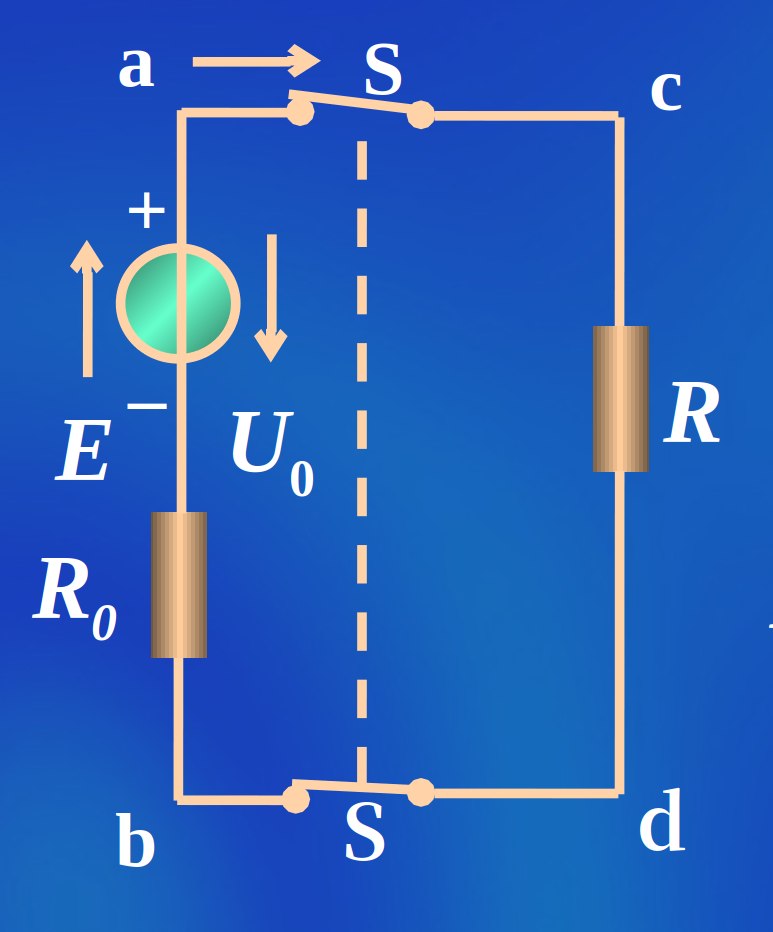 |
\(I = \frac{E}{R + R_0}\) | 有载状态: 开关S合上,电流I通过电阻R |
| 短路 | 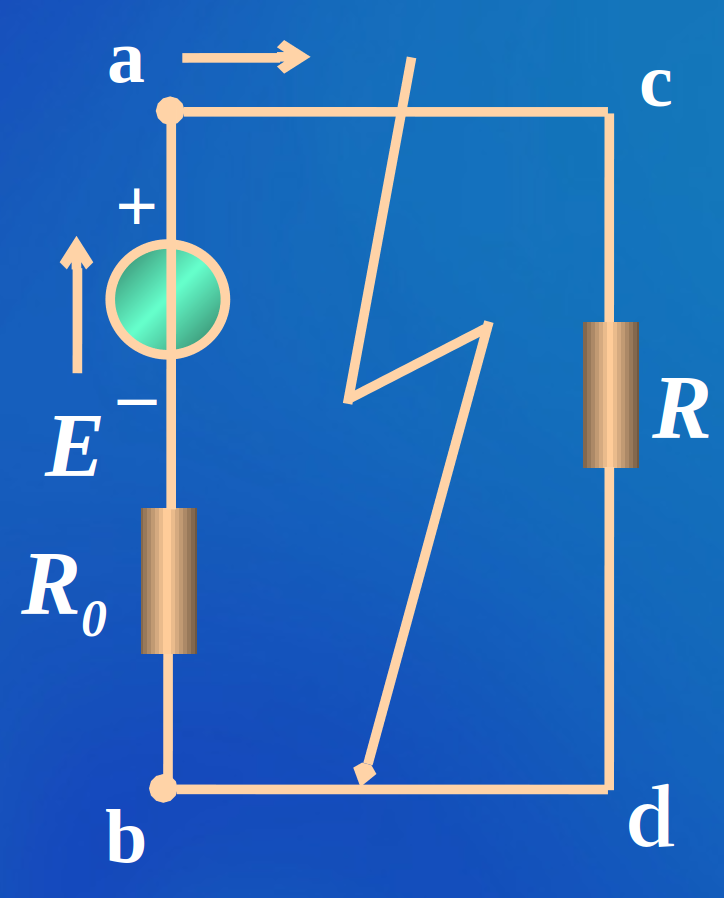 |
\(U = 0\) \(I_S = \frac{E}{R_0}\) | 短路状态: 电路的负载电阻为零 |
理想电路元件分类
电阻元件
-
电阻(R): 具有消耗电能特性的元件
-
相关公式
note: G是电导率
伏安特性
电阻原件上电压与电流间的关系
线性电阻
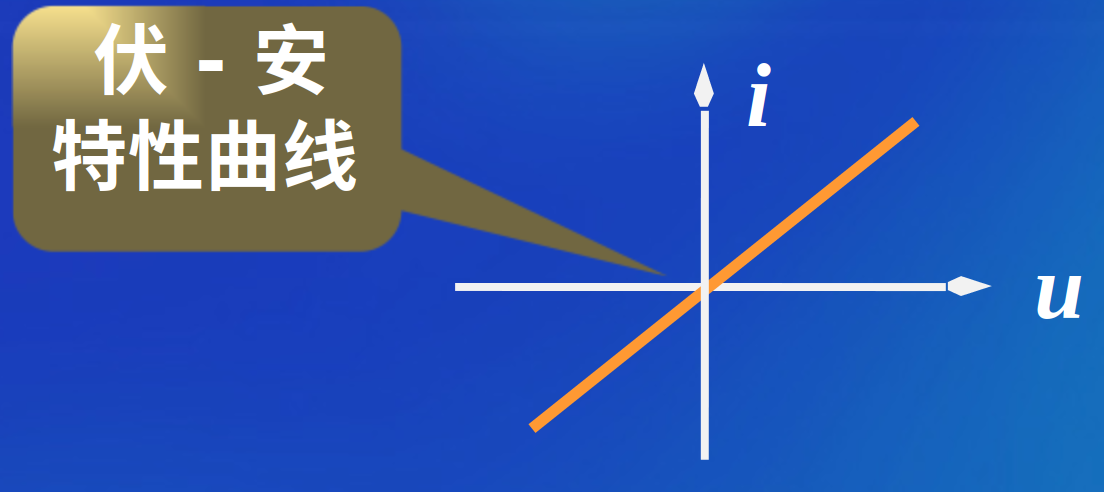
当 \(R = \frac{U}{I}\) 恒定不变时,称为线性电阻
非线性电阻
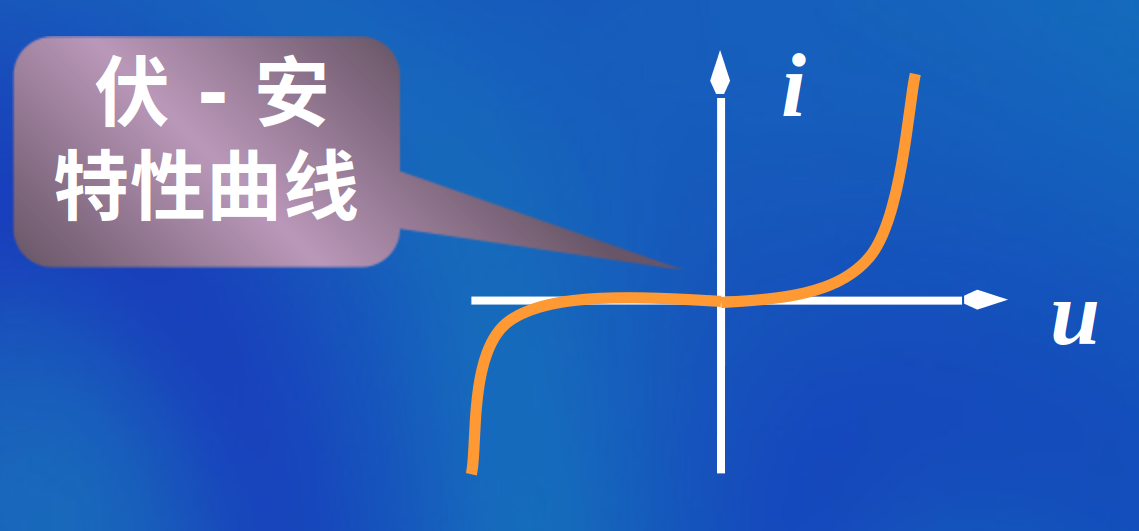
当电压与电流之间不是线性函数关系时,称为非线性电阻
电阻的计算
实际金属导体的电阻与导体的尺寸及材料的导电性能有关
| 符号 | 意义 |
|---|---|
| \(\rho\) | 电阻率 |
| \(l\) | 导体的长度 |
| \(S\) | 导体的横截面积 |
常见的电阻单位: 欧姆 (\(\Omega\)), 千欧 (\(k \Omega\))
电阻类型
- 普通金属膜电阻

- 绕线电阻

- 电阻排

- 热敏电阻

电感元件
-
电感: 能够存储磁场能量的元件
-
符号

-
自感系数
\[ L = \frac{N \times \Phi}{i} = \frac{\psi}{i} \]\(\psi\): 单位电流产生的磁通链
-
常见单位
\(H, mH\)
-
电感元件的基本伏安关系式
\[ u = L \frac{di}{dt} \]到变化的电流流经电感元件,电感元件会产生与电流变化相反的电动势
产生的电压是自感系数乘以电流的变化率
-
在直流电路中,电流的变化率为零,所以电感元件相当于一根无阻的导线
-
电感存储的磁场能量
\[ W_L = \frac{1}{2}Li^2 \]可以类比动能的表达式
\[ W = \frac{1}{2}mv^2 \]\(L\) 是相当于 \(m\) 的常量,由电感本身决定,\(i\) 相当于 \(v\) 都是描述运动的物理量,\(i\) 是电子的运动,而 \(v\) 是宏观物体的运动。
-
线圈自感系数的计算
线圈的电感与线圈的尺寸、匝数以及附近截至的导磁性能等有关
| 符号 | 意义 |
|---|---|
| \(\mu\) | 线圈附近截至的磁导率 (H/m) |
| \(S\) | 线圈的横截面积 (\(m^2\)) |
| \(l\) | 线圈的长度f (m) |
-
电感元件的常见类别
-
陶瓷电感

-
带有磁心的电感

-
铁氧体电感

电容元件
-
电容: 具有储存磁场能量特性的元件
-
电容的定义式
- 电容元件的伏安关系式
-
由于直流电路中电流的变化率为0,所以电容在直流电路中相当于开路
-
电容储存的电场能量
- 电容的计算
电容器的电容与尺寸介质的介电常数有关
| 符号 | 意义 |
|---|---|
| \(\varepsilon\) | 介质的介电常数 (F/m) |
| \(S\) | 两个极板相对的面积 ( \(m^2\) ) |
| \(d\) | 两个极板的距离 (m) |
-
常见的电容器
- 电解电容器

- 普通电容器

- 电力电容器

- 电解电容器
理想无源元件的伏安关系 -- 总结
note: u与i参考方向一致
| R | L | C |
|---|---|---|
| \(u = Ri\) | \(u = L\frac{di}{dt}\) | \(i = C\frac{du}{dt}\) |