CF743C

观察样例二，可以发现 \(n\) ， \(n+1\) ， \(n\times (n+1)\) 是一组合法的解。

那么如果正经地推，怎么推呢？

将 \(\frac {2}{n}\) 拆成 \(\frac {1}{n}+\frac {1}{n}\) ，然后令 \(x=\frac {1}{n}\) ，接下来就考虑如何构造 \(y,z\) 使得 \(\frac {1}{y}+\frac{1}{z}=\frac {1}{n}\)

根据小学学过的分数裂项，可知：\(\frac{1}{n}=\frac{n+1}{n\times (n+1)}=\frac{1}{n+1}+\frac{1}{n\times (n+1)}\)，所以 \(y=n+1,z=n\times (n+1)\)

网络

题目大意：\(n\times m\)的方格图，相邻的方格之间有边，需要构造一个最小生成树，使得它的直径为 \(d\) （\(n,m<=1000,d<=10^6\)），无解输出 \(NO\) 。

先考虑是否存在解。首先直径最多只能是 \(nm-1\) ，这个相当于用蛇形图把所有格点串起来。如果 \(n,m\) 全为偶数，那么直径最少是 \(n+m-1\) ；否则直径最少是 \(n+m-2\) 。直径最少时是王字图，可以借助下面的图理解一下。

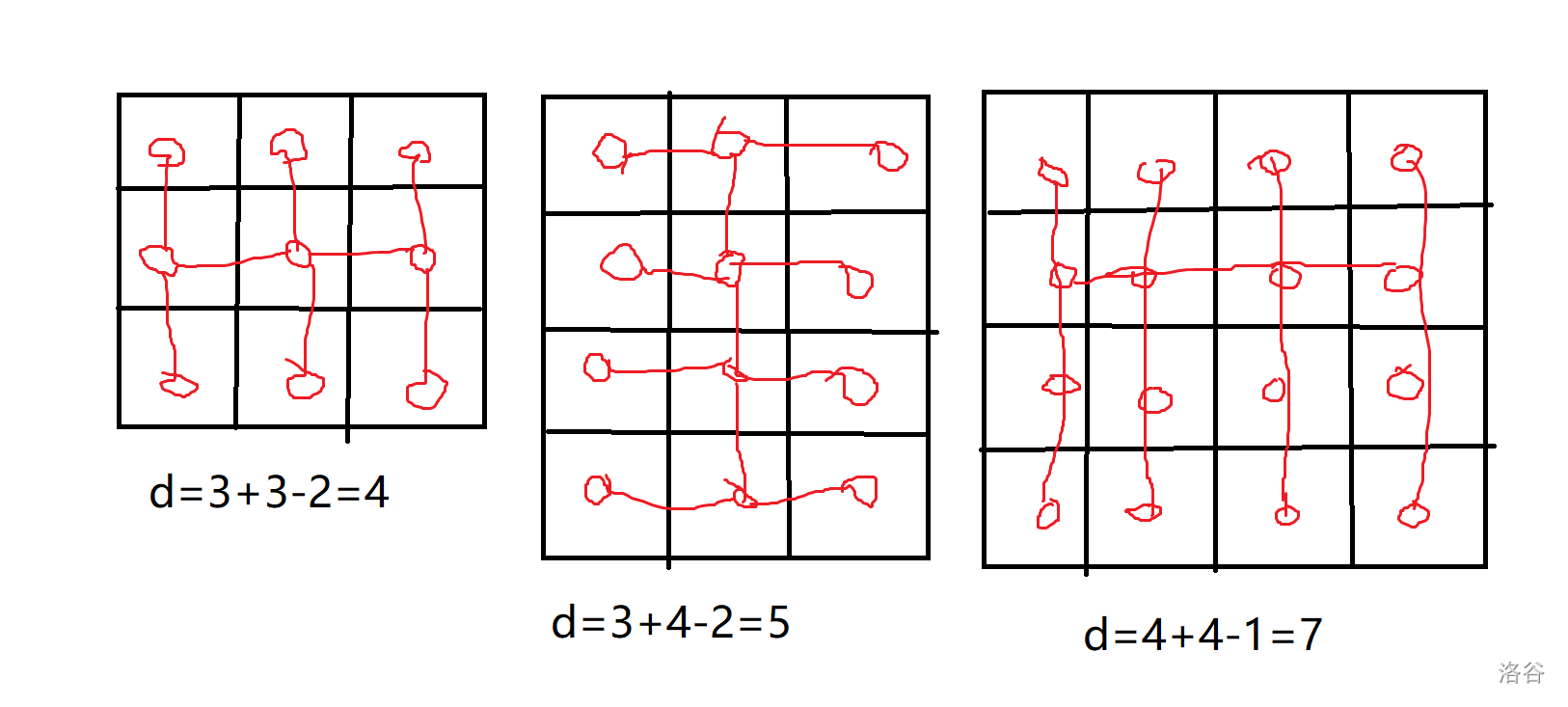
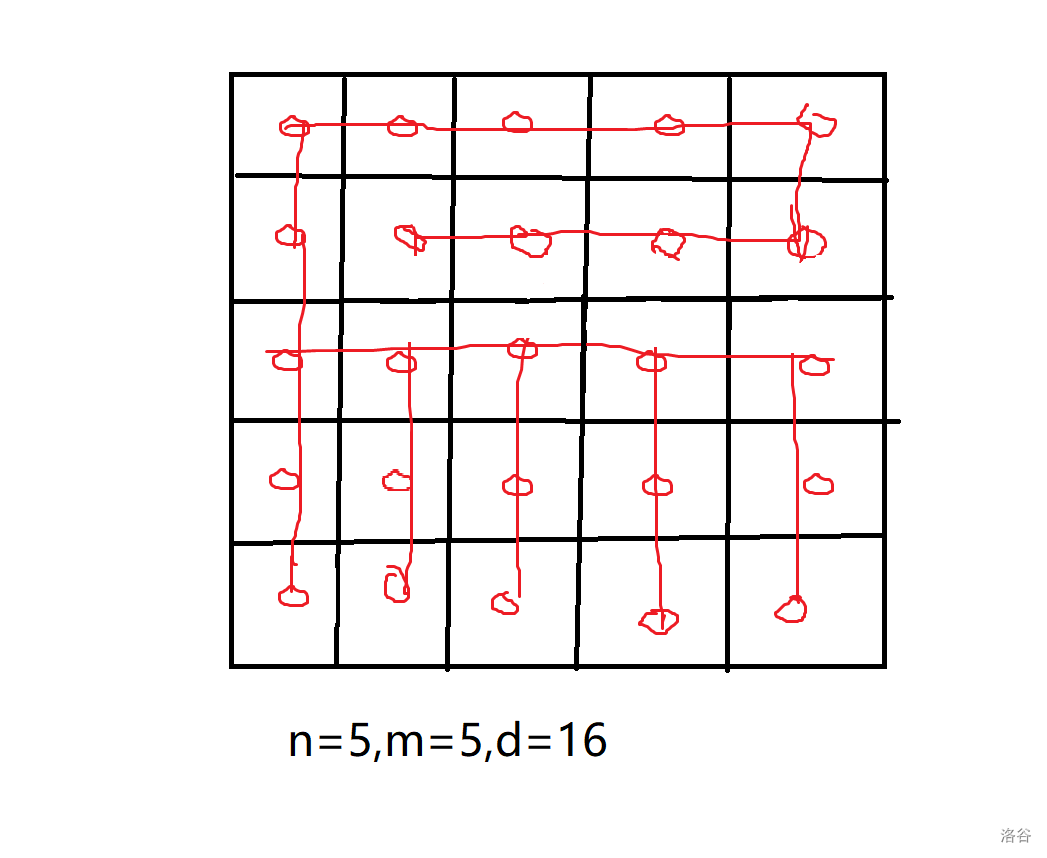
再考虑构造。当直径最小时为王字图，当直径最大时为蛇形图，因此构造时不妨将二者结合起来。具体而言，先将中间的一行设为“王”字的那一竖，然后从分别从左上角，右下角开始构造蛇，最后将王和蛇连起来。可以借助下图理解构造过程：

\(code:\)

void print(int x1,int y1,int x2,int y2){
    if(!tag)
        printf("%d %d %d %d\n",x1,y1,x2,y2);
    else
        printf("%d %d %d %d\n",y1,x1,y2,x2);
}
int main(){
    scanf("%d%d%d",&n,&m,&d);
    if(!(n&1)&&(m&1))
        swap(n,m),tag=1;//尽量让n是奇数
    if(n&1)//等价于：存在奇数
        minn=n+m-2;
    else
        minn=n+m-1;
    if(d>=n*m||d<minn){
        printf("NO\n");
        return 0;
    }
    printf("YES\n");
    mid=(n+1)>>1;
    z=d-minn;//直径比起最小情况还需要增加多少
    if(mid!=1&&m>1){//从左上角开始的蛇形
        x=1;y=1;
        if(!(n&1)&&!(m&1))
            ++z;//如果全是偶数，那么n也是偶数，那么mid会略靠上一些，蛇长度需要加一
        while(z){//只有比最小值多的部分用蛇形
            if(x&1){//奇数行向右
                if(y<m)//向右
                    print(x,y,x,y+1),vis[x][++y]=1,--z;
                else if(x<mid-1)//换行
                    print(x,y,x+1,y),vis[++x][y]=1,--z;
                else
                    break;
            }
            else{//偶数行向左
                if(y>2)//向左
                    print(x,y,x,y-1),vis[x][--y]=1,--z;
                else if(x<mid-1)//换行
                    print(x,y,x+1,y),vis[++x][y]=1,--z;
                else
                    break;
            }
        }
    }
    if(mid<n&&m>1){//从右下角开始的蛇形
        x=n;y=m;
        while(z){//只有比最小值多的部分用蛇形
            if((x&1)==(n&1)){
                if(y>1)//向左
                    print(x,y,x,y-1),vis[x][--y]=1,--z;
                else if(x>mid+1)//换行
                    print(x,y,x-1,y),vis[--x][y]=1,--z;
                else
                    break;
            }
            else{
                if(y<m-1)//向右
                    print(x,y,x,y+1),vis[x][++y]=1,--z;
                else if(x>mid+1)//换行
                    print(x,y,x-1,y),vis[--x][y]=1,--z;
                else
                    break;
            }
        }
    }
    for(int i=1;i<=m;++i){
        if(i<m)
            print(mid,i,mid,i+1);//“王”字的中间那一竖
        for(int j=mid-1;j>=1;--j){
            if(vis[j][i]) break;
            print(j,i,j+1,i);//扩展王，连接王与蛇
        }
        for(int j=mid;j<n;++j){
            if(vis[j+1][i]) break;
            print(j,i,j+1,i);//扩展王，连接王与蛇
        }
    }
    return 0;
}

Road to 1600

直接构造比较困难，所以我们可以考虑先暴力搜索出\(3\times 3\)的一种方案：

然后发现，当 \(n\) 大于 \(3\) 时，可以根据上面的方案螺旋构造出当前的方案。当 \(n=4\) 时，可以构造出如下方案：

数据规模更大时，仍然可以像这样螺旋构造，只需要注意当 \(n\) 为奇数时，从左下角开始螺旋构造；当 \(n\) 为偶数时，从右上角开始螺旋构造。

\(code;\)

signed main(){
    scanf("%lld",&n);
    a[1][1]=9;a[1][2]=5;a[1][3]=6;
    a[2][1]=7;a[2][2]=2;a[2][3]=8;
    a[3][1]=1;a[3][2]=3;a[3][3]=4;
    if(n<=2){
        printf("-1\n");
        return 0;
    }
    for(int i=4;i<=n;++i){
        cnt=0;
        if(i&1){
            for(int j=1;j<=i;++j)
                a[i][j]=++cnt;
            for(int j=i-1;j>=1;--j)
                a[j][i]=++cnt;
            sum[i-1]=cnt;
        }
        else{
            for(int j=1;j<=i-1;++j)
                a[j][i]=++cnt;
            for(int j=i;j>=1;--j)
                a[i][j]=++cnt;
            sum[i-1]=cnt;
        }
    }
    for(int i=n-1;i>=1;--i)
        sum[i]+=sum[i+1];
    for(int i=1;i<=n;++i,printf("\n"))
        for(int j=1;j<=n;++j){
            printf("%lld ",sum[max(i,j)]+a[i][j]);
        }
    return 0;
}