充分条件、必要条件、充要条件
逻辑条件的运用场景
充分条件与必要条件在现实生活中有广泛的运用。以下是一些常见的例子:
-
医疗诊断:
在医疗诊断中,医生常常根据患者的症状和检查结果来推断可能的疾病。
例如,如果一个患者出现胸痛和气短的症状,且心电图显示心肌缺血,那么医生可以推断该患者可能患有冠心病。这里,充分条件是胸痛和气短的症状以及心电图检查结果,必要条件是患者患有冠心病。 -
法律判决:
在法律判决中,法官通常根据证据和法律规定来判断被告人是否有罪。
例如,如果被告人被发现持有毒品,且没有合法的理由来解释这一点,那么法官可能会判定被告人有罪。这里,充分条件是被告人持有毒品且没有合法的理由,必要条件是被告人有罪。 -
决策分析:
在决策分析中,决策者通常考虑各种因素来评估不同方案的可能性、风险和收益。
例如,在选择投资项目时,投资者可能会考虑项目的盈利能力、可持续性以及市场需求等因素。这里,充分条件是投资项目的各种因素满足投资者的要求,必要条件是投资者选择该项目。
这些例子表明,充分条件与必要条件在生活中帮助我们进行推断、判断和决策。 了解充分条件和必要条件的含义和运用对于解决实际问题具有重要的意义。
背景知识
- 先了解命题、命题结构、真命题、假命题;
命题(proposition)
- 命题是陈述性语句或表达式,可以被判定为真或假。命题陈述某个主题或陈述某个事实,并且只有两种可能的逻辑状态:真(True)或假(False);
- 最基本的命题的结构必须包括
条件和结论; - 命题结构是指命题的组成方式或形式。命题结构包括命题中的
变量、连接词和量词等。通过改变命题结构中的变量的取值,我们可以得到不同的具体命题。例如,命题结构"P(x): x是偶数"中的变量是"x","P(x)"表示x是偶数。
什么是充分、什么是必要?
充分、必要(Necessity and sufficiency)是西方逻辑学科专用词,翻译过来之后,我们用固有的语言思维去套用在句子总会感觉怪怪的,这也不难怪。
所以不用太在意翻译过来的中文字和固有逻辑的冲突,只需要捋顺这个词的本质逻辑即可。
以前的西方人,也起了另一名字叫蕴含( → ),但其实意思还是一样的。
"蕴含"是指一个命题或条件可以推导出另一个命题或条件的关系。如果命题A蕴含命题B,那么当命题A成立时,可以推断出命题B也成立。
| 当命题 “若P则Q” 为真时,P称为Q的充分条件,Q称为P的必要条件。 |
因此:
当命题 “若P则Q” 与 “若Q则P” 皆为真时,P是Q的充分必要条件,同时,Q也是P的充分必要条件。
当命题 “若P则Q” 为真,而 “若Q则P” 为假时,我们称P是Q的充分不必要条件,Q是P的必要不充分条件,反之亦然。
基于对命题真假的推理,可以得出如下4种组合:
- 充分不必要
- 必要不充分
- 充分且必要
- 不充分且不必要
条件状态真值表
(注意!)实际上,真值表是根据两个命题的逻辑关系来判断两个命题的真假的工具,它建立的依据是逻辑关系。脱离逻辑关系的真值表没有任何意义。

意味着如果A为真,则B也为真;如果A为假,则对B没有任何影响。

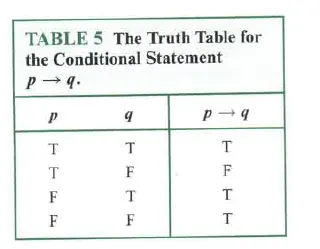
最后一条有点超出了我的认知,我查了一下,基于条件p和q都为假的假设。在这种情况下,我们可以确定p和q的否定命题为真。
我思考并总结了一下:假的条件推出假的结论,但是这个逻辑形式是真的。(这个假结论不要和总体的真假混淆)。
建议程序员都认真学习一下真值表,还是很有的。
分析过程技巧
先将命题解构成如下格式,
___ 是 ___ 的 ___ 条件 ?
可以把 ___替换成左,也可以替换成A:
左 --- 右
A --- B
条件 --- 结论
前件 --- 后件
A称为前提或前件,B称为结论或后件
命令的结构也可以是如下形式:
- 若……,则……
- 如果……,那么……
- 只要……,就……
- ...
得出结论的固定规律:
左 → 右 :充分 | 右 → 左 :必要
左 ↛ 右 :不充分 | 右 ↛ 左 :不必要
Reference
充分必要条件
https://zh.wikipedia.org/zh-hans/充分必要条件
逻辑符号表
https://zh.wikipedia.org/zh-cn/逻辑符号表