《北文的树形连通块dp》

ddl1no2home / 2023-09-03 / 原文

想看原文可以看这个

对于一些问题，让我们数颜色数，要知道数颜色数这个东西非常的不好维护。

往往我们四种解决方法：

直接暴力数
只数最后一个出现的（如果有什么性质的话）
容斥，减去算重的
将每个分开来计算贡献

本文着重讲解第三种和第四种。

P2664 树上游戏

先来一道例题。

首先我们考虑将每种颜色分开来计算，且计算不包含这种颜色的数量，最后用总数一减就好了。

我们可以先考虑一种颜色一种颜色枚举处理。

我们先看红色的点都是与根节点也暗色相同的点，我们假设根节点是最上面的那个点，那么假如把这些红色的点全部删掉，我们就会形成若干个连通块，这些连通块内部不管怎么走，都是不包含我们当前这种颜色的。

也就是说对于一种颜色我们需要计算他的子树大小减去子树中根节点鱼这个节点颜色相同的极大子树的大小，剩下的就是我们连通块的数量，不过需要注意，我们这样做，只能计算连通块不包含 $1$ 的情况，对于连通块包含 $1$ 的情况还要额外算一下贡献。

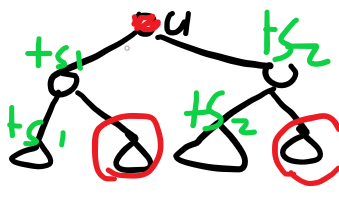
对于上图

假设对于当前节点 $u$ ，那么子树分别 $+s_1,s_2$

现在考虑多种颜色，我们发现每个点至多修改一种颜色，而其他颜色仍然不变，所以我们考虑每次只改与当前节点颜色相关的东西。

首先我们加数肯定不能像刚才那样一个一个子树里面的点枚举，然后加，考虑差分。

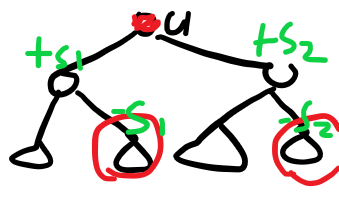
大概长成这样。

然后我们这题就做完了，理论做完了，不过实现起来有点麻烦就是了。

分析一下 $dfs$ 怎么写

点击查看代码

//sc[u] 表示颜色u在当前节点子树中的极大子树是多少
void dfs1(int u,int fa) {
	sz[u]=1; dfn[u]=++len;//记录字典序
	int c=col[u];
	for(int i=h[u];i;i=que[i].f) {
		int t=que[i].t;
		if(t==fa) continue;
		LL ls=sc[c];
		dfs1(t,u);
		sz[u]+=sz[t];
		LL xx=sz[t]-(sc[c]-ls);
		sc[c]+=xx;//加上连通块中数量
		cf[t]+=xx;//差分在第一个节点加
		while(e[c].size()&&dfn[e[c].back()]>dfn[u]) {//找到所有dfs序大于u的，全部打上S1标记，因为这代表在u子树中
			cf[e[c].back()]-=xx;
			e[c].pop_back();
		}
	}
	++sc[c];//加上自己
	e[c].push_back(u);
}

然后是全部代码，全部代码里面对于连通块含 $1$ 部分有讲解。

点击查看代码

#include<bits/stdc++.h>
typedef long long LL;

using namespace std;
const int MAXN=1e5+10;
LL n;
LL col[MAXN];
LL buc[MAXN],tot;
struct daduoli {
	LL f,t;
}que[MAXN*2];
LL cnt,h[MAXN];
void add(int f,int t) {
	que[++cnt].f=h[f];
	que[cnt].t=t;
	h[f]=cnt;
}
LL sz[MAXN],dfn[MAXN],len,sc[MAXN],cf[MAXN];
vector<LL> e[MAXN];
void dfs1(int u,int fa) {
	sz[u]=1; dfn[u]=++len;
	int c=col[u];
	for(int i=h[u];i;i=que[i].f) {
		int t=que[i].t;
		if(t==fa) continue;
		LL ls=sc[c];
		dfs1(t,u);
		sz[u]+=sz[t];
		LL xx=sz[t]-(sc[c]-ls);
		sc[c]+=xx;
		cf[t]+=xx;
		while(e[c].size()&&dfn[e[c].back()]>dfn[u]) {
			cf[e[c].back()]-=xx;
			e[c].pop_back();
		}
	}
	++sc[c];
	e[c].push_back(u);
}
LL sum[MAXN];
void dfs2(int u,int fa) {
	sum[u]=sum[fa]+cf[u];
	for(int i=h[u];i;i=que[i].f) {
		int t=que[i].t;
		if(t==fa) continue;
		dfs2(t,u);
	}
}
int main () {
	scanf("%lld",&n);
	for(int i=1;i<=n;++i) {
		scanf("%lld",&col[i]);
		if(!buc[col[i]]) ++tot;
		buc[col[i]]=true;
	}
	for(int i=1;i<n;++i) {
		LL x,y;
		scanf("%lld%lld",&x,&y);
		add(x,y);
		add(y,x);
	}
	dfs1(1,0);
	for(int i=1;i<=100000;++i) {
		if(buc[i]) {
			cf[1]+=n-sc[i];//求剩下的
			for(auto t:e[i]) {
				cf[t]-=n-sc[i];//也是差分
			}
		}
	}
	dfs2(1,0);
	for(int i=1;i<=n;++i) {
		printf("%lld\n",tot*n-sum[i]);
	}
	return 0;
}

[ABC163F] path pass i

直接对每个颜色求，那甚至连差分都不用了，直接计算贡献，不过他这里的路径有点奇怪。

总路径是 $n+n*(n-1)/2$

然后一个大小为 $x$ 的连通块贡献是 $x*(x-1)$

对于 $i\sim i$ ，自己走到自己的简单路径另外讨论一下，因为不太好计算。

点击查看代码

#include<bits/stdc++.h>
typedef long long LL;

using namespace std;
const int MAXN=2e5+10;
LL n;
LL col[MAXN];
LL buc[MAXN],tot;
struct daduoli {
	LL f,t;
}que[MAXN*2];
LL cnt,h[MAXN];
void add(int f,int t) {
	que[++cnt].f=h[f];
	que[cnt].t=t;
	h[f]=cnt;
}
LL sz[MAXN],dfn[MAXN],len,sc[MAXN],cf[MAXN];
LL ans[MAXN];
vector<LL> e[MAXN];
void dfs1(int u,int fa) {
	sz[u]=1; dfn[u]=++len;
	int c=col[u];
	for(int i=h[u];i;i=que[i].f) {
		int t=que[i].t;
		if(t==fa) continue;
		LL ls=sc[c];
		dfs1(t,u);
		sz[u]+=sz[t];
		LL xx=sz[t]-(sc[c]-ls);
		sc[c]+=xx;
		ans[col[u]]-=xx*(xx-1)/2;
		while(e[c].size()&&dfn[e[c].back()]>dfn[u]) {
			e[c].pop_back();
		}
	}
	++sc[c];
	e[c].push_back(u);
}
int main () {
	scanf("%lld",&n);
	for(int i=1;i<=n;++i) {
		ans[i]=n+n*(n-1)/2;
	}
	for(int i=1;i<=n;++i) {
		scanf("%lld",&col[i]);
	}
	for(int i=1;i<n;++i) {
		LL x,y;
		scanf("%lld%lld",&x,&y);
		add(x,y);
		add(y,x);
	}
	dfs1(1,0);
	for(int i=1;i<=n;++i) {
		LL xx=n-sc[i];
		ans[i]-=(xx-1)*xx/2;
		ans[i]-=n;
	}
	for(int i=1;i<=n;++i) ++ans[col[i]];
	for(int i=1;i<=n;++i) {
		printf("%lld\n",ans[i]);
	}
	return 0;
}