【无线通信基础】第三章点对点通信中的检测以及分集

AAZeusSkyThunder / 2023-09-03 / 原文

David Tse在此章介绍了无线通信中不可避免会遇到的问题：衰落信道造成的误码率上升，以及对抗衰落信道的方式——分集。
整个章节的思路非常清晰，首先介绍Rayleigh衰落信道下的检测，并且通过计算分析了衰落信道下的误码率为何远超过AWGN信道，由此引出了深度衰落的现象以及对抗的方式：分集；之后便介绍了分集的思想以及具体实现方式。

1. Rayleigh衰落信道下的检测

先从最简单的情况分析——平坦衰落信道(flat fade channel,即不存在多径)。

\[\tag{1.1}y(m)=h(m)x(m)+w(m) \]

其中$h(m)\sim\mathcal{CN}(0,1)$，$w(m)\sim\mathcal{CN}(0,N_0)$。

若使用未编码的信号进行传输，如使用BPSK：

\[\begin{cases} x_1=a\\x_0=-a \end{cases} \]

那么即使没有AWGN噪声，接收信号也是无法解调的，因为发送$x_0$和$x_1$时，接收端信号分布相同，都是服从$\mathcal{CN}(0,a^2)$，无法区分。

若使用简单的正交调制：

\[x_A=\left[ \begin{matrix} x(0)\\ x(1) \end{matrix} \right]=\left[\begin{matrix} a\\ 0 \end{matrix}\right]\quad x_B=\left[\begin{matrix}0\\a\end{matrix}\right] \]

可以很直观的推出最大似然估计的准则：

\[\begin{cases} x_A&\Lambda(y)\geq 0\\ x_B&\Lambda(y)<0 \end{cases} \]

其中$\Lambda(y)$为对数似然比：

\[\Lambda(y)=ln(\frac{f(y|x_A)}{f(y|x_B)}) \]

而判决准则也易于推出：

\[|y(0)|^2>|y(1)|^2->x_A \]

因为$y$服从圆对称复高斯分布，因此$y^2$服从指数分布，均值分别为$a^2+N_0$和$N_0$，误判的概率可以表示为：

\[p_e=P{|y(0)|^2<|y(1)|^2|x_A}=[2+\frac{a^2}{N_0}]^{-1} \]

若记$a^2/2N_0$为信噪比$SNR$，则

\[p_e=\frac{1}{2(1+SNR)} \]

这一结果意味着若是想要达到$p_e=10^{-3}$则至少需要$SNR=500(27dB)$，这种信噪比的需求太高了！

为何会出现这种情况，会不会是衰落信道导致的呢？基于这种猜测，我们下面分析无衰落信道情况下的系统，即AWGN系统下的误码率。

1.1 AWGN信道下误码率分析

对于AWGN信道，不需要进行正交调制，判决的准则也十分简单，当用BPSK发送信号$\pm a$时，充分估计量为$\mathcal{Re}(y)$，即根据$y$的符号判断发送信号，系统模型可以表示为：

\[y(m)=x(m)+w(m) \]

误码率为：

\[p_e=P{y<0|x=a}=\mathcal{Q}(\frac{a}{\sqrt{N_0/2}})=\mathcal{Q}(\sqrt{2SNR}) \]

其中$SNR=\frac{a^2}{N_0}$（是平坦衰落信道正交调制的两倍），达到$p_e=10^{-3}$仅需要7dB。
为何会有如此巨大的差异？分析几种可能

信道随机性导致：不知道信道增益的大小
~~正交调制/非相干检测的锅（我也不知道为什么是你的问题，先写上）~~
衰落信道就是逊啦！遇到就会变差
还有啥，我也想不到了。

基于上述三种假象的可能，先试着排除前两者：若是接收端能对信道进行估计（用导频、训练序列等whatever），每次信道都是确定性的了，此种情况下系统的performance如何呢？

1.2 Rayleigh衰落信道+相干检测

已知信道增益的情况下，可以进行相干检测，系统模型可以表示为

\[y=hx+w \]

$h$是已知的了，充分估计量可以表示为：

\[r:=\mathcal{Re}\left\{\frac{h^*}{|h|}y\right\}=|h|x+z \]

误码率可以推出：

\[\tag{3.1}p_e=\mathcal{Q}(\frac{a|h|}{\sqrt{N_0/2}})=\mathcal{Q}(\sqrt{2|h^2|SNR}) \]

此时，系统的信噪比和AWGN信道情况下一致$SNR=a/N_0$。若是对信道衰落求平均，因为$h\sim\mathcal{CN}(0,1)$

\[p_e=\mathbb{E}_h\{\mathcal{Q}(\sqrt{2|h^2|SNR})\}=\frac{1}{2}\left(1-\sqrt{\frac{SNR}{1+SNR}}\right)\approx\frac{1}{4SNR} \]

(这里对$\sqrt{\frac{SNR}{1+SNR}}$做了Taylor展开：$\sqrt{\frac{SNR}{1+SNR}}=1-\frac{1}{2SNR}+\mathcal{O}(\frac{1}{SNR^2})\dots$）
效果依然很差，若是需要获得$p_e=10^{-3}$，相较于AWGN信道，Rayleigh衰落信道下相干检测的情况仍需要额外的17dB信噪比增益。WHY？

通过上述分析可以看出，问题不在于接收机不知道信道状态信息(CSI)，而是在于衰落信道的信道增益是随机的，并且有很大一部分几率信道处在深度衰落(deep fade)的情况。
根据(3.1)的误码率公式，因为Q函数的拖尾在$(x>1)$后衰减的很快，而$x<1$时则下降的不快，因此，当$|h|^2SNR>1$时，误码率下降很快，而$|h|^2SNR\leq 1$时，星座点之间的间隔会变得和噪声标准差在同一个量级，此时误码率很大。

\[P\{|h|^2SNR\leq 1\}=\int_0^{1/SNR}e^{-x}dx=\frac{1}{SNR}+\mathcal{O}(\frac{1}{SNR^2}) \]

（所以深度衰落是啥？深度衰落就是$|h|^2<1/SNR$的情况)所以说，对于高信噪比情况下错误发生的原因主要是信道处于深度衰落，而并非加性噪声过大导致。

2. 分集

上述衰落信道中误码率较高的原因主要是通信的可靠性主要依靠于一条路径的强度，而这条路径发生深度衰落的概率较大。自然地可以想到能够通过将信号通过多条独立信道，只要有一条路径的信道强度足够，就可以保证可靠通信。

时间分集：通过编码和交织在时间上构建多个独立信道
空间分集：通过多天线构建多个独立信道
频率分集：通过在多个频段通信，构建多个独立信道

2.1 时间分集

Time diversity is achieved by averaging the fading of the channel over time.

还是以最简单的平坦衰落信道为例，设传输一段长度为L的码字为$\mathbf{x}=[x_1,\dots,x_L]^T$，让$x_l$发送的间隔足够大，因此每个信道增益$h_l$都可以认为是独立的（这里$L$称作分集支路(diversity branches)的数量）

repetition code

最简单的情况是采用重复编码，即将一个符号重复$L$次发送，相当于时间上扩展了$L$倍。即：

\[\mathbf{y}=\mathbf{h}x_1+\mathbf{w} \]

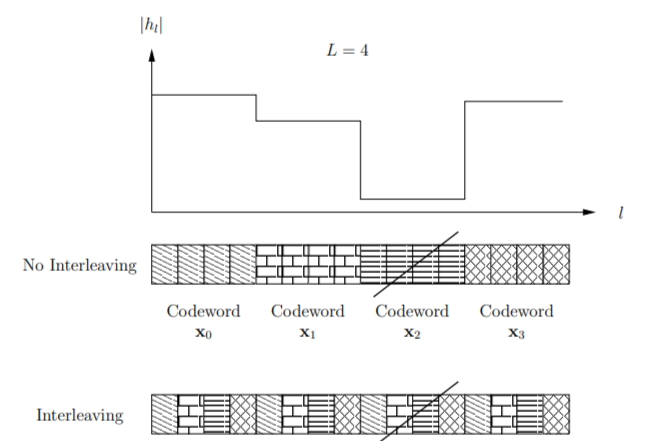
上图给出了采用重复编码情况下发送4个码字且分集之路数量为4的情况，在信号发送前需要进行交织，这样每个码字都会经历不同的分集支路。
若进行相干检测（即信道增益在接收机可以提前估计出来），采用最大比合并器(按照各个支路信道强度加权然后合并)，充分估计量可以表示为：

\[\frac{h^*}{||\mathbf{h}||}\mathbf{y}=||\mathbf{h}||x+\frac{h^*}{||\mathbf{h}||}\mathbf{w} \]

若是采用BPSK，则误码率可以表示为：

\[p_e=\mathcal{Q}(\sqrt{2||\mathbf{h}||SNR}) \]

其中信噪比$SNR=a/N_0$和之前的情况一样，但是$||\mathbf{h}||=\sqrt{\sum|h_l|^2}$，因为$h_l$是复数，所以相当于$2L$个高斯随机变量平方相加后开根号，属于$\chi^2$分布，有$2L$的自由度,其概率密度函数为：

\[f(x)=\frac{1}{(L-1)!}x^{L-1}e^{-x}\quad x\geq 0 \]

而对信道增益求期望，平均误码率可以求出：

\[\begin{align} p_e&=\int_0^\infty\mathcal{Q}(\sqrt{2xSNR})f(x)dx\\ &=(\frac{1-\mu}{2})^L\sum_{l=1}^{L-1}(\matrix{{L-1+L}\\{l}})(\frac{1+\mu}{2})^l \end{align} \]

其中$\mu=\sqrt{\frac{SNR}{1+SNR}}$，求近似可以得到

\[p_e=\left(\matrix{{2L-1}\\{L}}\right)\frac{1}{(4SNR)^L} \]

显然降低了较多，类似地可以评估深度衰落发生的概率：

\[P\left\{||h||^2\leq \frac{1}{SNR}\right\}=\frac{1}{L!}\frac{1}{SNR^L} \]

tips:这种估计较为粗略，只是阶数是正确的，即，当所有$L$个之路的信道都陷入深度衰落时，深度衰落才会发生！