Self-Adjusting Top Tree（SATT）学习笔记

\(\mathtt{1}\) 树收缩

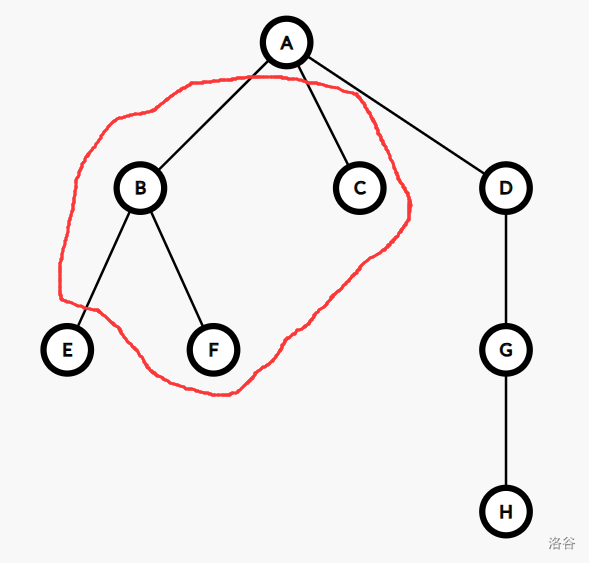
树收缩的两个核心操作为 \(\operatorname{compress}\) 和 \(\operatorname{rake}\)。

\(\mathtt{1/1}\) \(\operatorname{compress}\)

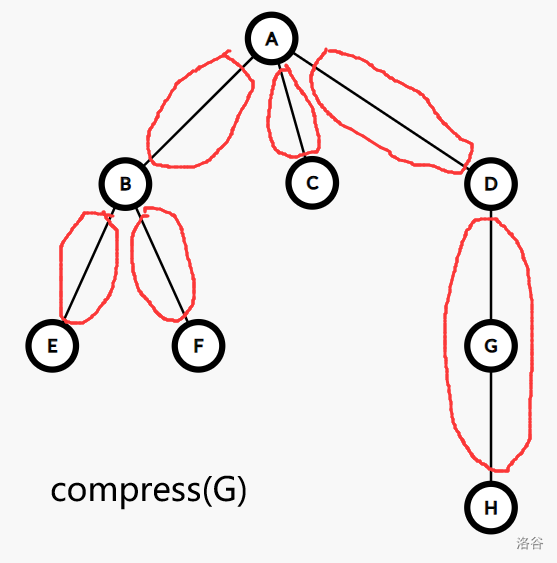
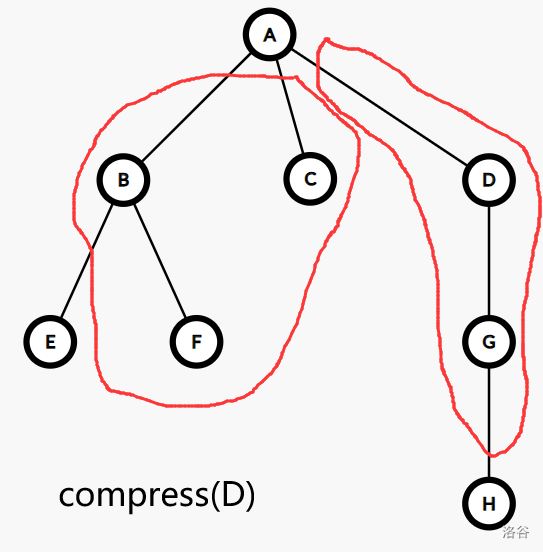
\(\operatorname{compress}\) 操作指定了树上的一个度为 \(2\) 的节点 \(v\)，设 \(v\) 的两个邻点为 \(u,w\)，则 \(\operatorname{compress}(v)\) 将点 \(v\) 与边 \((u,v),(v,w)\) 的信息合并记录到新建的边 \((u,w)\) 上，并删去点 \(v\) 与边 \((u,v),(v,w)\)：

（图源 negiizhao 的博客）

\(\mathtt{1/2}\) \(\operatorname{rake}\)

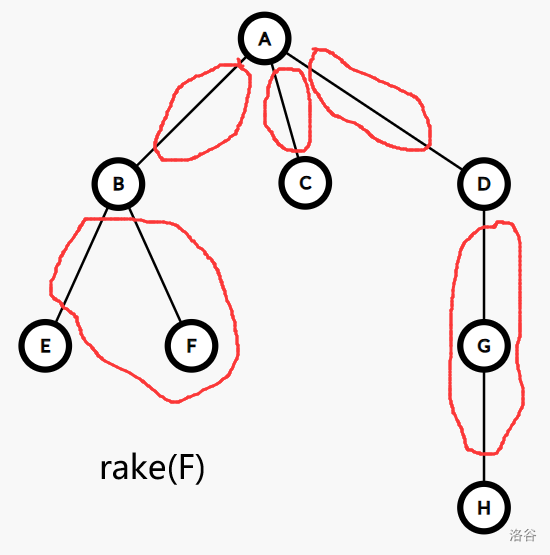
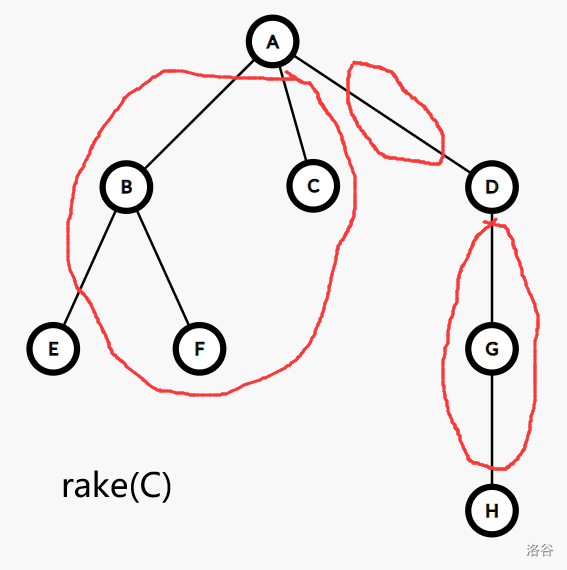
\(\operatorname{rake}\) 操作指定了树上的一个度为 \(1\) 的节点 \(v\)，设 \(v\) 的邻点为 \(x\)，而 \(x\) 的另一个邻点为 \(w\)（\(w\ne v\)），则 \(\operatorname{rake}(v)\) 将点 \(v\) 与边 \((v,x)\) 的信息合并记录到边 \((x,w)\) 上，并删去点 \(v\) 与边 \((v,x)\)：

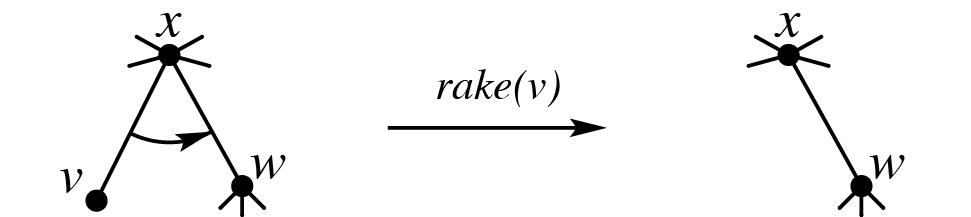
（图源 negiizhao 的博客）

不难发现，\(\operatorname{compress}\) 操作与 \(\operatorname{rake}\) 操作足以将一棵树收缩成一条边。

以下是一个可能的树收缩的过程：

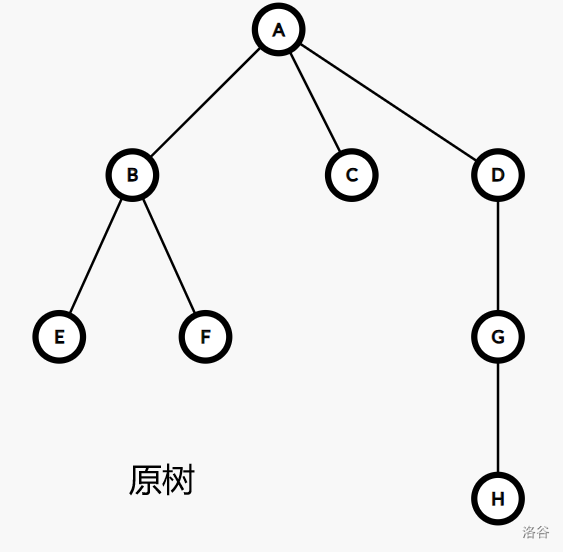
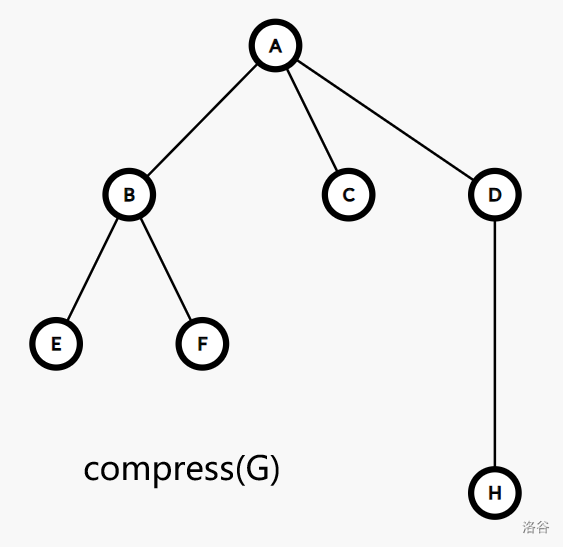
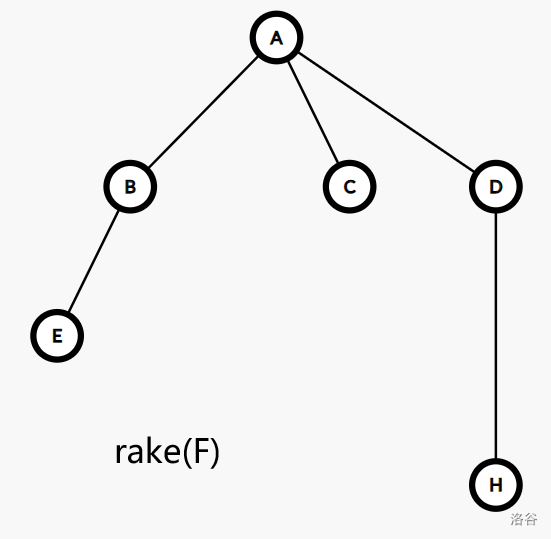
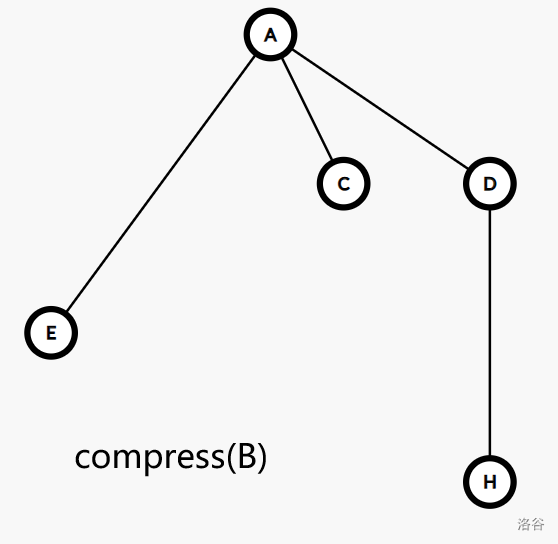
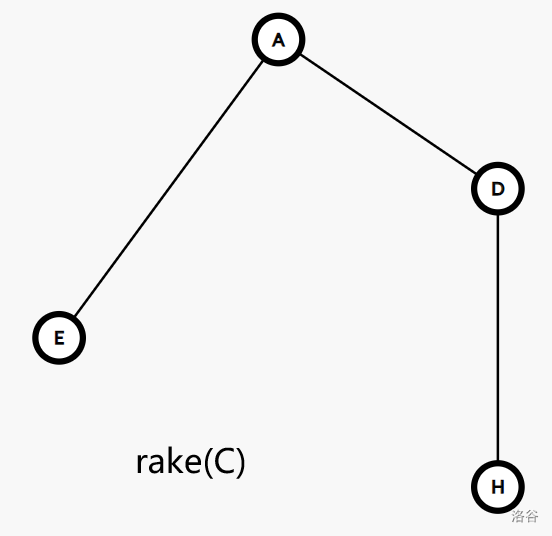
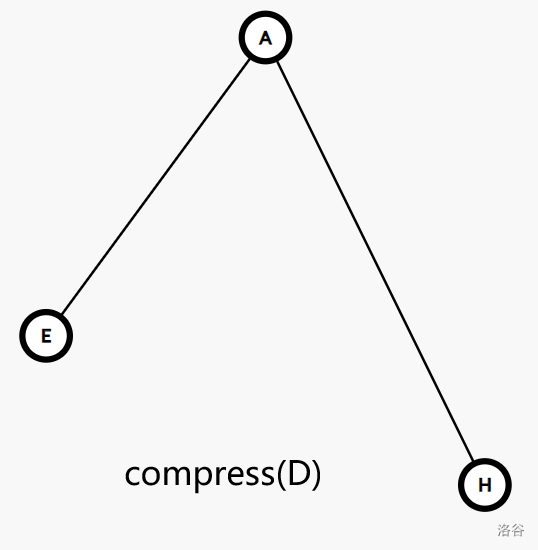
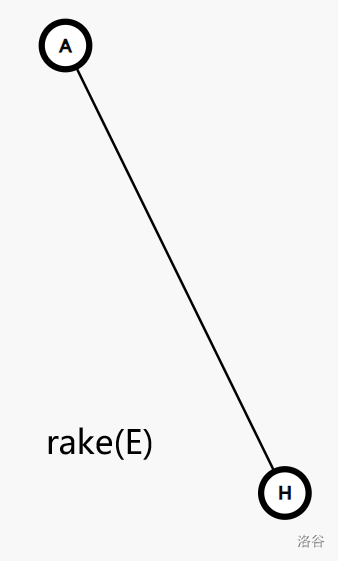
为了更好的刻画收缩过程中每条边蕴含的结构，我们引入一个概念：

\(\mathtt{2}\) 簇

以下记原树为 \(T\)，收缩过程中的某棵树为 \(T'\)。

则对于 \(T'\) 中的一条边，其蕴含的信息有两种：一种是它自身（前提是它存在于 \(T\)）的信息，另一种则是通过 \(\operatorname{compress}\) 和 \(\operatorname{rake}\) 操作合并到它上面的点或边包含的信息。

例如，对于

这棵树中的边 \((A,E)\)，它蕴含着原树中的这些信息：

（注意边 \((A,E)\) 在原树中并没有蕴含点 \(A,E\)）

容易发现，边 \((A,E)\) 在原树中蕴含的点和边再加上点 \(A,E\) 就组成了原树的一个联通子图，我们将这种连通子图称为簇。点 \(A,E\) 被称为这个簇中的端点，该簇中的其他点被称作这个簇中的内点，该簇中的边被称作这个簇中的内边。

簇有以下性质：

• 一个簇只维护内点和内边的信息；
• 一个簇对应着原树的收缩过程中某个时刻的一条边；
• 一个簇总是有两个端点，即为其对应的原树的收缩过程中某个时刻的一条边的两个端点；
• 一个簇的两个端点在原树上的路径被称为簇路径；
• 一个簇中内边连接的两个点仍在簇中，内点的邻点仍在簇中，但端点可能会有不在簇中的邻点。

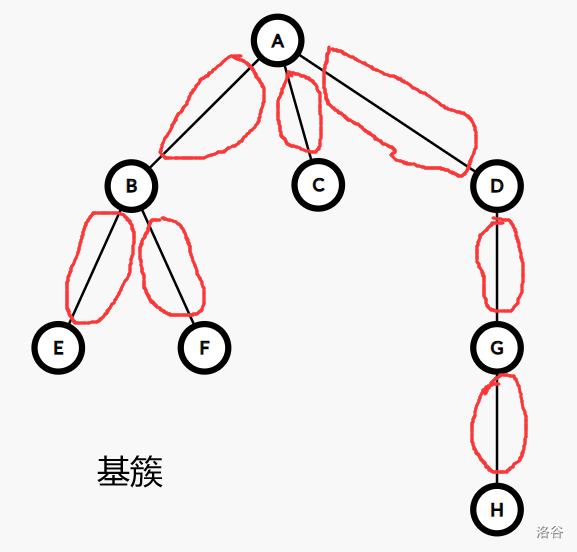
在原树中，每条边都对应着一个只包含它自身的簇，我们将其称为基簇。

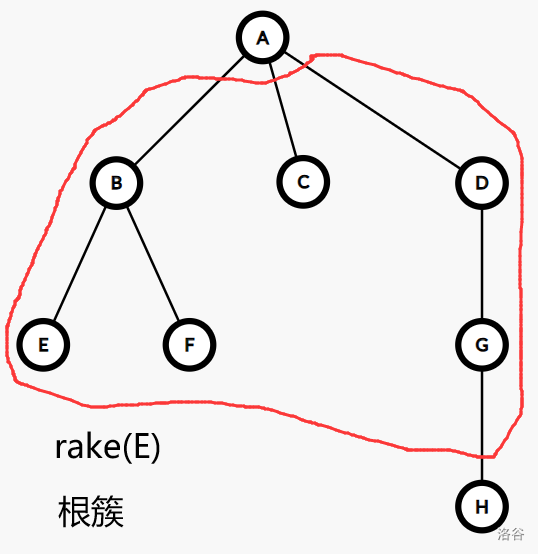
在原树收缩到的最终的边中，这条边对应着一个包含整棵树的簇，我们将其称为根簇。

从簇的视角，不难发现 \(\operatorname{compress}\) 和 \(\operatorname{rake}\) 的本质都是在原树上合并两个簇，因此树收缩的过程就是将基簇合并为根簇的过程。

于是，我们可以从簇的视角来观察树收缩的过程：

\(\mathtt{3}\) Top Tree

Top Tree 是一棵二叉树，其维护了一棵树的一个收缩过程，其中每个节点都表示着树中的一个簇（或收缩过程中某棵树的一条边），一个节点的左右儿子对应的簇可以通过 \(\operatorname{compress}\) 或 \(\operatorname{rake}\) 操作合并成该节点对应的簇。其叶节点为基簇，根节点为根簇，通常我们使用一个簇的两个端点来代指这个簇。

以上文的收缩过程与原树可以得到如下的 Top Tree：

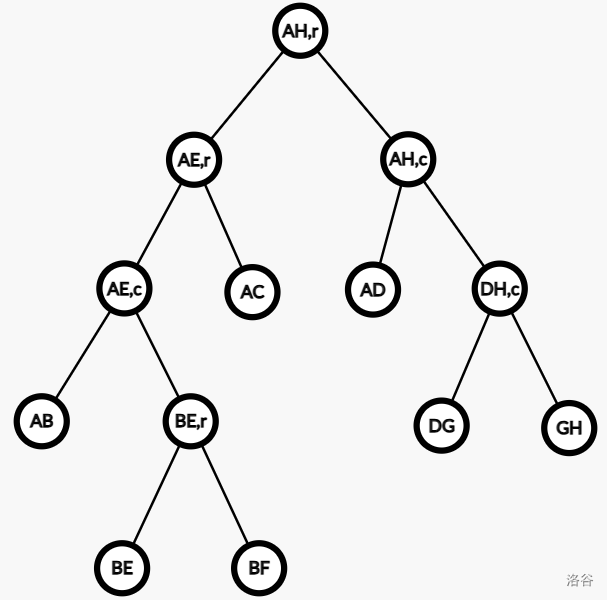
（非叶节点的后缀表示它的构造方法，\(r\) 表示 \(\operatorname{rake}\)，\(c\) 表示 \(\operatorname{compress}\)）

Top Tree 通过维护收缩操作与簇的信息来实现较复杂的操作，根据具体实现又分为 SATT，WCTT 等。本文将只介绍更易实现的 SATT。

\(\mathtt{4}\) SATT

\(\mathtt{4/1}\) 构建

我们指定一个度为 \(1\) 的点 \(r\) 为根，再任意指定另一个度为 \(1\) 的点 \(x\)，我们称这两个点之间的路径为根路径，它也是根簇的簇路径，在构建出来的 Top Tree 中，根簇的两个端点即为 \(r\) 和 \(x\)。

如果只有根路径，这就是一条链，我们可以通过一系列的 \(\operatorname{compress}\) 操作将其收缩成一个簇，我们将该过程得到的 Top Tree 称作 compress tree。

但除了 \(r\) 和 \(x\)，根路径上的其他点 \(i\) 可能会有一些不在根路径上的邻点 \(y\)，我们递归地将以 \(y\) 为根的子树收缩成一个簇（构建出 Top Tree），然后通过一次 \(\operatorname{compress}(y)\) 操作将点 \(y\) 和边 \((y,i)\) 加入当前的簇，同时使 \(i\) 变成该簇的端点；特殊的，如果 \(y\) 没有子节点，则我们不需要进行任何操作。接着通过 \(\operatorname{rake}\) 操作将以 \(i\) 为端点的不在根路径上的簇合并，过程中得到的 Top Tree 称作 rake tree。

最后我们将 rake tree 通过 \(\operatorname{rake}\) 操作尽可能晚的合并到根路径上（接到 compress tree 上），即可得到最终的 Top Tree。

例如，在

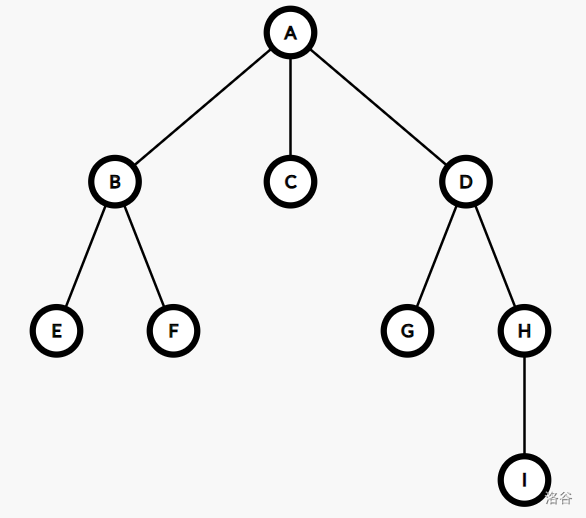
这棵树中，我们可以令 \(C\) 为根，并指定另一个点为 \(E\)，并递归地对其他子树操作，可以得到这样的结构：

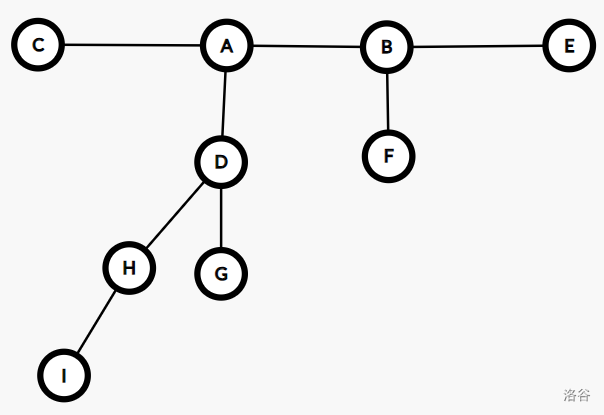
我们需要递归构建出以 \(D\) 为根的子树的 Top Tree，而其又要递归构建出以 \(H\) 为根的子树的 Top Tree，其只有一个根节点 \((H,I)\)，然后我们进行 \(\operatorname{compress}(H)\) 操作使点 \(D\) 称为该簇的端点，然后进行 \(\operatorname{rake}(I)\) 操作即可将以 \(D\) 为根的子树收缩成一条边，其 Top Tree 为：

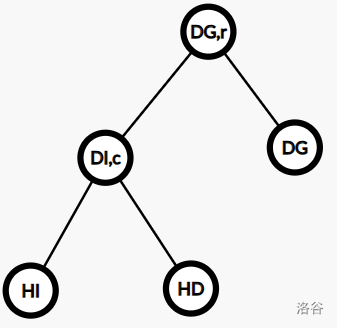
然后我们进行一次 \(\operatorname{compress}(D)\) 操作，将该簇的端点变为 \(A\)，就得到了 \(A\) 的 rake tree：

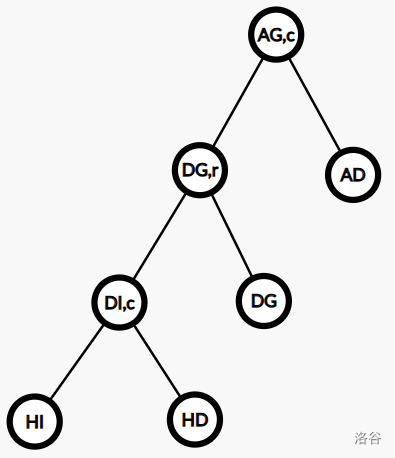
由于 \(F\) 没有子节点，所以我们可以直接保留它，于是 \(B\) 的 rake tree 简单的由根节点 \(BF\) 构成。

最后我们构建出 compress tree：不妨先进行 \(\operatorname{compress}(A)\)，但在那之前我们需要先执行 \(\operatorname{rake}(G)\) 将 \(A\) 的 rake tree 合并到根路径上，接着通过 \(\operatorname{rake}(F)\) 将 \(B\) 的 rake tree 合并到根路径上，最后 \(\operatorname{compress}(B)\) 即可得到最终的 Top Tree：

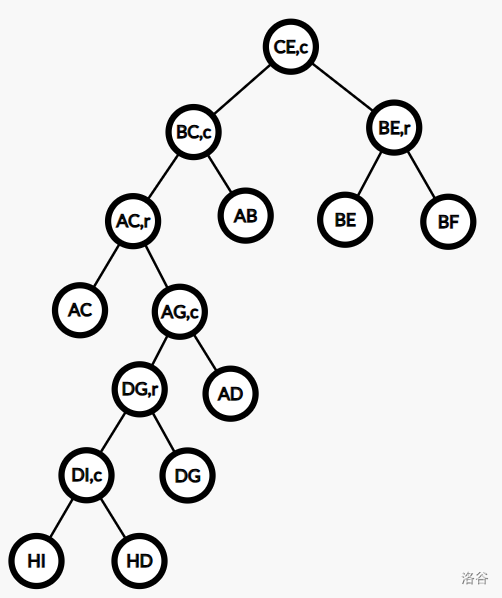
事实上，我们可以将 compress 节点改为三叉的：一个 compress 节点 \(x\) 由三个儿子构成，其含义即为：先将中儿子 \(\operatorname{rake}\) 到簇路径上，然后 \(\operatorname{compress}(x)\) 合并两个簇。

那么原来的 SATT 三度化后变为：

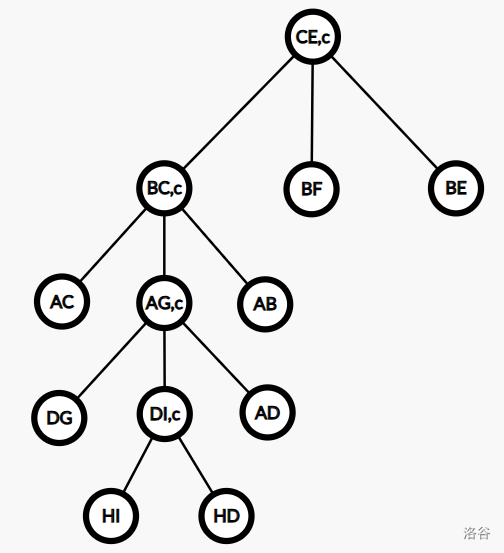
如果我们不需要维护边上的信息，可以删去基簇部分。

我们可以任意旋转（中儿子不变）compress 节点或 rake 节点（注意不能旋转基簇，因为它既不是 compress 节点也不是 rake 节点），因此我们可以使用 splay 来维护 SATT。