01-Trie - 解决异或问题的 Trie
前言
Trie 树就是所谓的字典树(前缀树),每个节点都是一个字母,用来解决单词匹配的问题。
而 01-Trie 是一种特殊的字典树,其中的节点的值都在 \({0, 1}\) 中。
01-Trie 可以用来解决一部分异或问题。
建树
向 01-Trie 中插入的是一个二进制数,根据题目的不同,可以从高位向低位插,也可以从低位向高位插。
现在我们从高位往低位插。
第一步我们需要把所有的数字的二进制位对齐。
比如我们要插入 11,4 和 14,11 的二进制是 1011,14 是 1110,4 是 100,我们就需要把 4 补为 0100。
接下来就可以采取普通字符串插入普通 Trie 的方式插入了。最终的插入结果应该是这样的(红色是根,黑色是 \(1\),白色是 \(0\))。
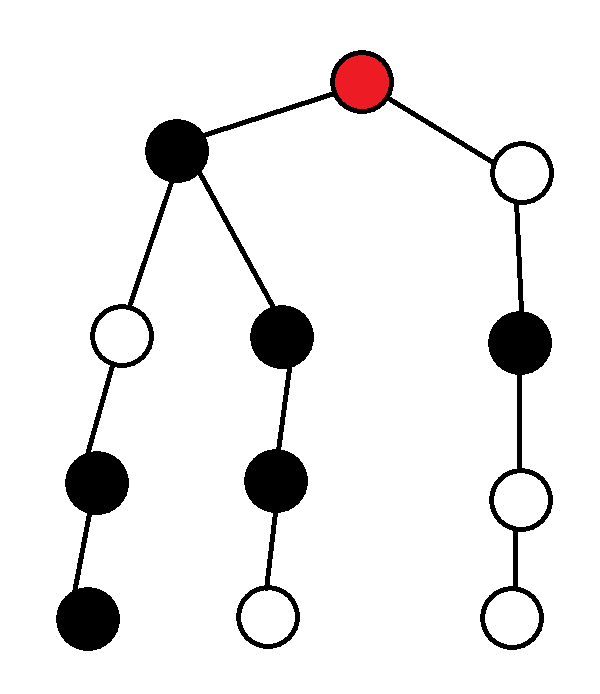
维护异或极值
给你一个集合 \(A\),你需要从其中挑出两个数使他们的异或和最大。
乍一看可以使用线性基解决,实际上会发现线性基并不好做,线性基适合的类型是从集合中挑出任意多数求极值。
这个时候就需要使用 01-Trie 了。