割点、割边、双连通分量
目录
- 割点、割边
- 双连通分量
- 求双连通分量 - tarjan算法
- 例题
割点、割边
割点 和 割边 就是特定的点和边,满足在图中删去其后,会使得图的连通分支数增加
例如下图中点 0, 1, 5, 7 就是割点(图中加粗),边 12、05、78、79 就是割边
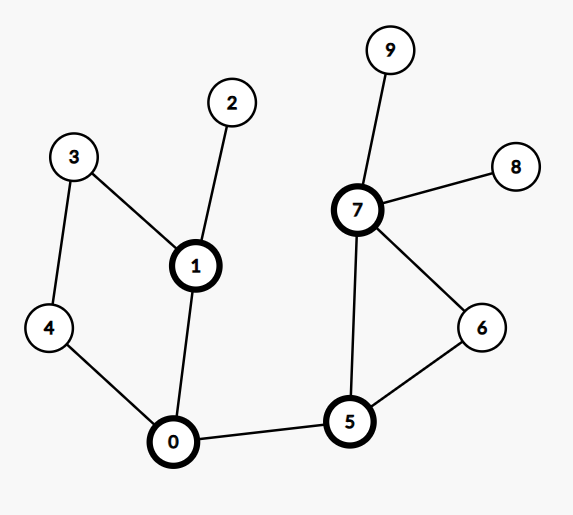
双连通分量
双连通分为点双连通和边双连通
点双连通:在一个连通图中任选两点,如果它们之间至少存在两条“点不重复”的路径,称为点双连通
边双连通:在一个连通图中任选两点,如果它们之间至少存在两条“边不重复”的路径,称为边双连通
点双连通图可以理解为没有割点的连通图,边双连通可以理解为没有割边的连通图
双连通分量
点双连通分量:一个图中的点双连通极大子图
边双连通分量:一个图中的边双连通极大子图
双连通分量可以缩图,边双缩成树,点双缩成 block tree