【Leetcode刷题记录】1、买钢笔和铅笔的方案数；2、一个图中连通三元组的最小度数；3、带因子的二叉树

Archigenius / 2023-09-01 / 原文

1、买钢笔和铅笔的方案数

题目：给你一个整数 total ，表示你拥有的总钱数。同时给你两个整数 cost1 和 cost2 ，分别表示一支钢笔和一支铅笔的价格。你可以花费你部分或者全部的钱，去买任意数目的两种笔。

请你返回购买钢笔和铅笔的 不同方案数目 。

思路：枚举法。

假设 total 最多可以买 n 支钢笔，则令 i = 0 ... n 枚举购买 i 支钢笔剩下的钱最多可以买多少支铅笔。此时公式为 j = (total - cost1 * i) / cost2。则当购买 i 支钢笔时，一共有 j + 1 种方案。

 1 class Solution {
 2 public:
 3     long long waysToBuyPensPencils(int total, int cost1, int cost2) {
 4         long long res = 0;
 5         int cnt = 0;
 6         while(cost1 * cnt <= total) {
 7             res += (total - cost1 * cnt) / cost2 + 1;
 8             cnt++;
 9         }
10         return res;
11     }
12 };

2、一个图中连通三元组的最小度数

题目：给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [u_i, v_i] ，表示 u_i 和 v_i之间有一条无向边。

一个 连通三元组 指的是三个节点组成的集合且这三个点之间两两有边。

连通三元组的度数 是所有满足此条件的边的数目：一个顶点在这个三元组内，而另一个顶点不在这个三元组内。

请你返回所有连通三元组中度数的 最小值 ，如果图中没有连通三元组，那么返回 -1 。

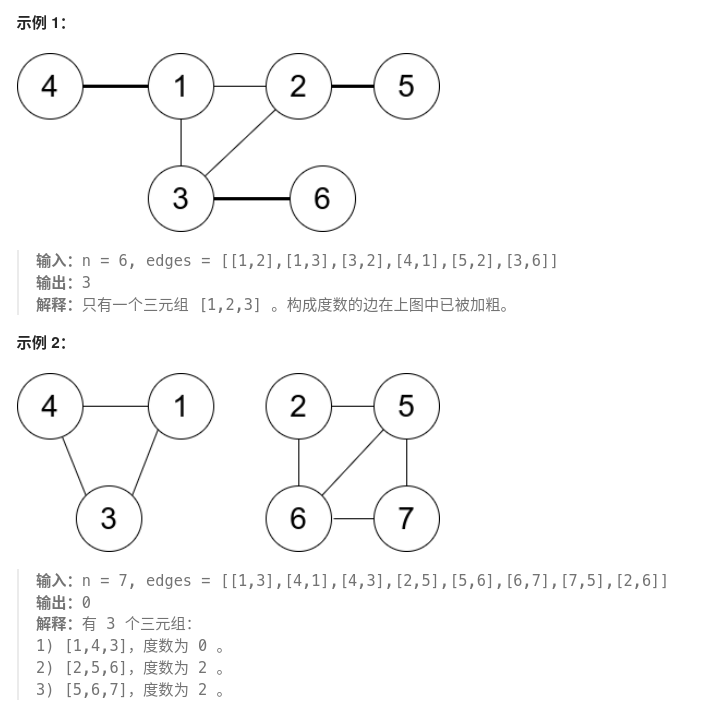
思路：遍历所有的连通三元组

创建一个二维 vector 数组记录节点的无向边，创建一个一维 vector 数组记录节点的度（即该节点有几条无向边）。

从小到大遍历所有节点计算每个连通三元组的度数，具体的做法是：假设三元组的节点分别是 i 、j 、k，则这个三元组的度数就是 i 、j、 k的度数和减去 6（6是构成三元组的边数，三条边每条都乘2）

代码：C++

 1 class Solution {
 2 public:
 3     int minTrioDegree(int n, vector<vector<int>>& edges) {
 4         vector<vector<int>> index(n+1,vector<int>(n+1,0));
 5         vector<int> degree(n+1,0);
 6         for(auto const& edge : edges){
 7             int x = edge[0], y = edge[1];
 8             index[x][y] = 1;    //无向边
 9             index[y][x] = 1;
10             ++degree[x];        //每个节点的度数 +1
11             ++degree[y];
12         }
13         int res = edges.size();
14         //遍历每个连通三元组
15         for(int i = 1; i < n; ++i) {
16             for(int j = i + 1; j <= n; ++j) {
17                 if(index[i][j] == 1){
18                     for(int k = j + 1; k <=n; ++k){
19                         if(index[i][k] == 1 && index[j][k] == 1){
20                             res = min(res,degree[i]+degree[j]+degree[k] - 6);
21                         }
22                     }
23                 }
24             }
25         }
26         return res == edges.size() ? -1 : res;
27     }
28 };

3、带因子的二叉树

题目：给出一个含有不重复整数元素的数组 arr ，每个整数 arr[i] 均大于 1。

用这些整数来构建二叉树，每个整数可以使用任意次数。其中：每个非叶结点的值应等于它的两个子结点的值的乘积。

满足条件的二叉树一共有多少个？答案可能很大，返回对 10⁹ + 7 取余的结果。

思路：动态规划。双指针。

先将 arr 数组排序，因为每个节点的子结点一定要比自身小！

然后动态规划计算以每个节点作为根节点时，共有多少种二叉树。具体的做法是：假设以第 i 个节点作为根节点，那么则从 [0 ... i-1] 找到两个节点，使得两个节点的值的乘积等于该节点的值；

然后做一次判断，如果这两个节点相等，则作为左右子结点不能互换，如果这两个节点不相等，则作为左右子结点可以互换。

代码：C++

 1 class Solution {
 2 public:
 3     int numFactoredBinaryTrees(vector<int>& arr) {
 4         sort(arr.begin(),arr.end());
 5         int n = arr.size();
 6         vector<long long> dp(n,1);
 7         long long res = 0, mod = 1e9 + 7;   //防止res过节，预先设置为long long类型
 8         for(int i = 0; i < n; ++i){
 9             for(int left = 0, right = i - 1; left <= right; ++left){
10                 while(left <= right && static_cast<long long>(arr[left]) * static_cast<long long>(arr[right]) > arr[i]){
11                     right--;
12                 }
13                 if(left <= right && arr[left] * arr[right] == arr[i]){
14                     if(left == right){
15                         dp[i] += (dp[left] * dp[right]) % mod;
16                     } else {
17                         dp[i] += (dp[left] * dp[right] * 2) % mod;
18                     }
19                 }
20             }
21             res = (res + dp[i]) % mod;
22         }
23         return res;
24     }
25 };