§3. 函数极限存在的条件
掌握归结原理、单调有界原理（只适用于四种单侧极限）和柯西准则。能够利用归结原理和柯西准则判断一个函数极限不存在。
注意每种趋向方式中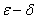
语言的不同。
重点习题：第1、2、3、4题。
海因里希·爱德华·海涅 (Heinrich Eduard Heine) 1821.3.16-1881.10.21
德国数学家。生于柏林，卒于哈雷市。1838年到柏林大学、哥廷根大学攻读，是高斯、狄利克雷的学生。1842年在柏林大学获得哲学博士学位。1844年任教于波恩大学，1848年成为特别教授，同年九月被聘为哈雷-维滕贝格大学教授，1864-1864年任校长。先后被选为普鲁士科学院通讯院士、哥廷根科学协会会员。1877年，在高斯诞辰纪念日获得高斯奖章以表彰他对数学的贡献。
主要成就
1、阐述了一致收敛的概念，证明了连续函数的一致收敛定理。
2、独立发现并利用了海涅定理（1895年，波莱尔证明了有限覆盖定理，这就是著名的波莱尔覆盖定理。由于海因里希·爱德华·海涅在关于一致连续的证明中也利用了这个性质，所以这个定理也有人称之为海涅-波莱尔定理），建立了沟通数列极限与函数极限的桥梁。
3、给出了无理数的算数定义。
出版著作：《球面函数指南》（Handbuch der Kugelfunctionen，1861年）
个人生活：1850年，海因里希·爱德华·海涅与一位柏林商人的女儿苏菲沃尔夫结婚，这对夫妇有五个孩子,四个女儿和一个儿子。