平衡二叉树（Binary Banlanced Tree)

ajn-zuiniu / 2023-08-30 / 原文

　　对于搜索树来说，不同的插入顺序会导致树的结构不一样，最终导致查找效率不一样。经过计算，发现左右子树比较平衡的树查找效率比较高。

　　平衡因子（Balance Factor，BF） BF(T)=hl-hr ，hl、hr表示树T的左右子树的高度。

　　平衡二叉树（Binary Balanced Tree) (AVL)树空树，或者左右子树高度相差不超过1 ，即|BF(T)|<1。

　　平衡二叉树在删除插入中，其平衡性可能会被破坏，下面我们就平衡二叉树的调整进行讨论：

一、RR旋转

　　新节点插入在不平衡“发现者”的左子树的左子树上。

　　如图，当节点插入在B的左子树上（可以在B的左子树上的任何位置，也可以作为B的左子树），A的平衡因子大于1，平衡性破坏，以A做为“发现者”，进行RR旋转。

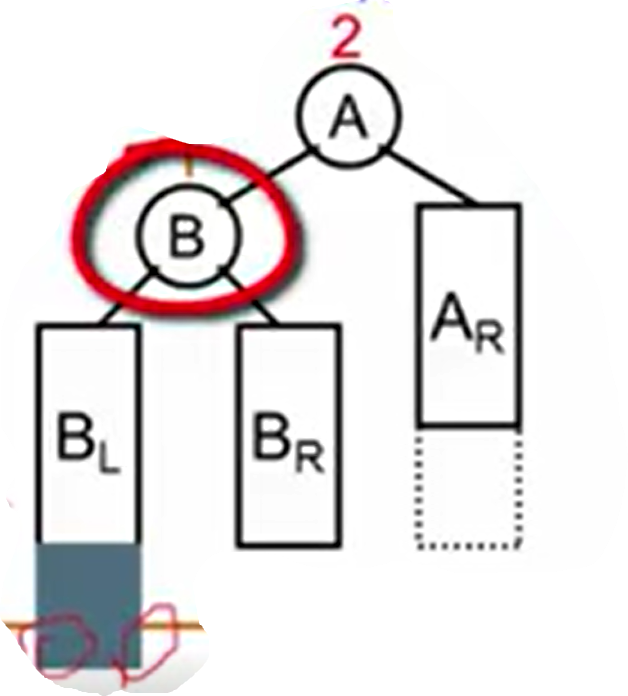
　　我们将发现者A的左儿子B（这里B是一定存在的）作为新的根节点，A比B大作为B的新右儿子，原来的B的右子树因为在A的左子树下，比A小，所以现在作为A的左儿子。

二、LL旋转

　　与RR旋转同理，新节点插入在不平衡“发现者”的右子树的右子树上。

　　如图，当节点插入在B的右子树上（可以在B的右子树上的任何位置，也可以作为B的右子树），A的平衡因子小于-1，平衡性破坏，以A作为“发现者”，进行LL旋转。

　　我们将发现者A的右儿子B（这里B是一定存在的）作为新的根节点，A比B小作为B的新左儿子，原来的B的左子树因为在A的右子树下，比A大，所以现在作为A的右儿子。

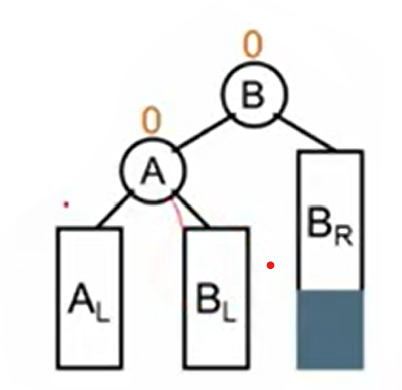
三、LR旋转

　　新节点插入在不平衡“发现者”的左子树的右子树上。

　　如图，当节点插入在B的右子树上（可以在B的右子树上的任何位置，也可以作为B的右子树），A的平衡因子大于1，平衡性破坏，以A作为“发现者”，进行LR旋转。

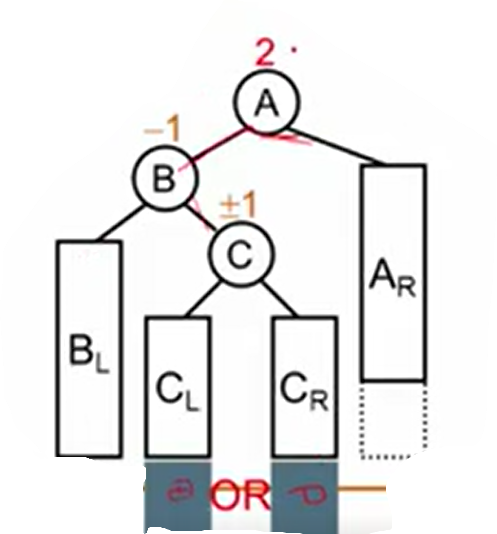
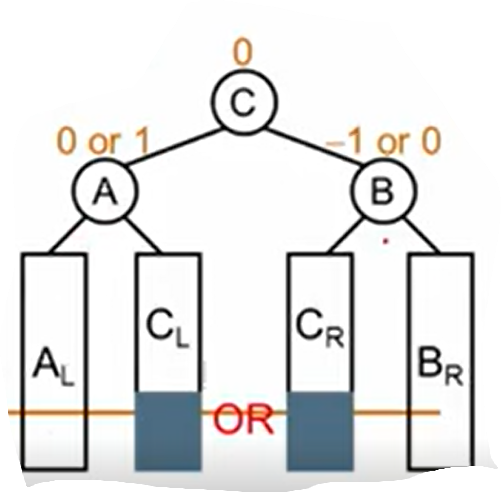
　　我们A、B、C中的中间值C作为新的根节点。A比C大作为C的新右儿子，B比C小作为C的新左儿子。原来C的左子树在B的右子树下，比B大，作为B的右子树，原来的C的右儿子在A的左子树下，作为A的左子树。

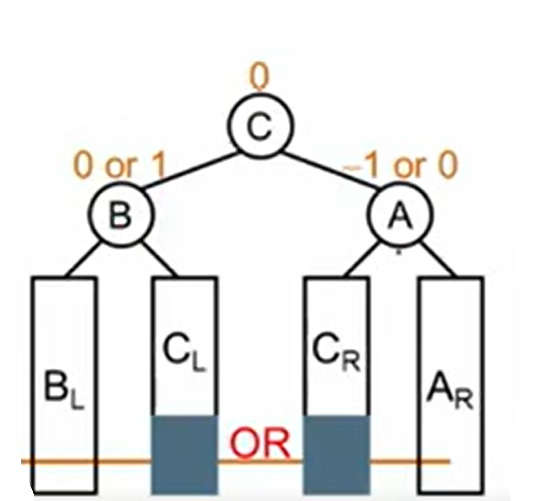
四、RL旋转

　　同LR旋转，新节点插入在不平衡“发现者”的右子树的左子树上。

　　如图，当节点插入在B的左子树上（可以在B的右子树上的任何位置，也可以作为B的右子树），A的平衡因子小于-1，平衡性破坏，以A作为“发现者”，进行RL旋转。

　　我们A、B、C中的中间值C作为新的根节点。A比C小作为C的新左儿子，B比C大作为C的新右儿子。原来C的右子树在B的左子树下，比B小，作为B的新左子树；原来的C的左儿子在A的右子树下，作为A的新右子树。

五、代码实现

　　1.求树高：树高是树中节点的最大层数。这里可以用递归先求左右子树的树高，取最大值+1，及当前树的树高。

　　2.RL旋转可以这这么实现：将B做RR旋转，这样麻烦节点（破坏平衡性的节点）就从左子树的右子树旋转到了左子树的左子树，再做LL旋转即可。

　　3.插入的时候，怎么知道新节点的下一个递归去了下个节点的左子树还是右子树？用数值进行比较就能判断。

 1 struct AVLNode{
 3     int data;
 4     AVLNode* left;
 5     AVLNode* right;
 6 };
 7 
 8 AVLNode* LL( AVLNode* u)
 9 {
10     AVLNode* t=u->left;
11     u->left=t->right;
12     t->right=u;
13     return t;
14 }
15 AVLNode* RR( AVLNode* u)
16 {
18     AVLNode* t=u->right;
19     u->right=t->left;
20     t->left=u;
21     return t;
22 }
23 AVLNode* LR( AVLNode* u)
24 {
26     AVLNode* t=u->left->right;
27     AVLNode* tb=u->left;
28     tb->right=t->left;
29     u->left=t->right;
30     t->left=tb;
31     t->right=u;
32     return t;
33 }
34 AVLNode* RL( AVLNode* u)
35 {
37     AVLNode* t=u->right->left;
38     AVLNode* tc=u->right;
39     tc->left=t->right;
40     u->right=t->left;
41     t->right=tc;
42     t->left=u;
43     return t;
44 
45 }
46 int getHeight( AVLNode* u)
47 {
48     if( u==NULL ) return 0;
49     return max( getHeight(u->left) ,getHeight(u->right) )+1;
50 }
51 AVLNode* Insert( AVLNode* u,int x)
52 {
53     if(u==NULL)
54     {
55         u=(AVLNode*)malloc( sizeof(struct AVLNode));
56         u->left=u->right=NULL;
57         u->data=x;
58     }else{
59 
60         if( x < u->data )
61         {
62             u->left=Insert( u->left, x );
63 
64             if( getHeight(u->left) - getHeight(u->right) > 1 )
65             {
66                 if( x < u->left->data ) u=LL(u);
67                 else u=LR(u);
68             }
69 
70         }
71         else
72         {
73             u->right=Insert(u->right,x);
74 
75             if( getHeight(u->left) - getHeight(u->right) < -1 )
76             {
77                 if( x > u->right->data ) u=RR(u);
78                 else u=RL(u);
79             }
80 
81         }
82     }
83     return u;
84 
85 }