NOIP训练赛 #3
T1 幸运数字Ⅱ
有 \(Q\) 个询问,每次给定一个区间 \(L,R\) 求区间内满足如下条件的 \(x\) 的个数:
\(x\) 为质数或者 为两个质数的积
【数据范围】
\(L,R\leq 10^7,Q \leq 10^5\)
题解
欧拉筛预处理出 \(10^7\) 以内满足条件的数的个数,做一遍前缀和即可
时间复杂度 \(O(10^7+Q)\)
T2 小树精灵

【数据范围】
\(1\leq n\leq 3000\)
题解
考虑到如果三个点之间距离相同,那么它们必然距离一个点距离相同(树上不存在环),故考虑枚举每个树上节点 \(x\) ,分别计算以 \(x\) 为根时各个节点的深度,然后用类似 \(01\) 背包的技巧将每个子树上相同深度的节点合并起来并统计贡献即可,用倒序枚举的原因是为了防止一棵子树内的节点重复贡献自己(选了自己两次及以上),而多棵子树之间可以互相贡献,故考虑倒序枚举
时间复杂度 \(O(n^2)\)
T3 滑道

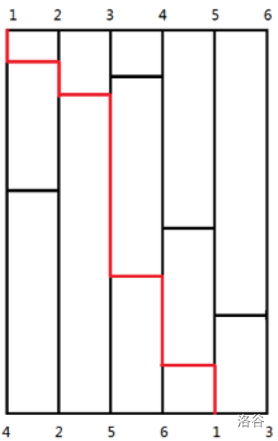
【数据范围】
\(1\leq n\leq 10^5,1\leq m\leq 10^6\)
题解
诈骗但是很好的思维题
对于第一问:考虑每一次经过一个横着的滑道,必然有两个相邻的球会互换位置,故直接枚举交换即可
对于第二问:考虑每一次智能互换两个相邻的球,那么最少交换次数就是这个序列里的逆序对的个数,树状数组维护即可
时间复杂度 \(O(nlogn)\)
T4 Dove 的疑惑

【数据范围】
\(n\leq 10^5,\prod_{i=1}^nm_i\leq 10^{18},1\leq m_i\leq 10^{18}\)
题解
T5 K直径生成树
有 \(n\times m\) 个点排成 行 列,坐标 \(i,j\) 表示的是第 \(i\) 行第 \(j\) 列的点。
如果两个点 \(A(x_1,y_1),B(x_2,y_2)\) 的距离\(|x_2-x_1|+|y_2-y_1|=1\) ,则 \(A\) 和 \(B\) 之间有边权为 \(1\) 的边相连。
给定整数 \(k\),构造一个这个图的生成树,使生成树的直径恰好有 \(k\) 条边
【数据范围】
\(1\leq n,m\leq 10^3\)
题解
第一次做构造题诶
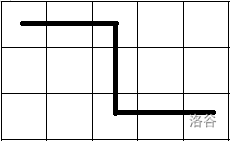
首先考虑当前直径 \(k\) 是否合法,很容易想到上界和下界的两种情况:
下界:
上界:
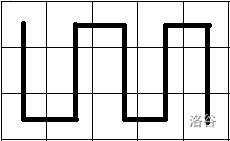
当 \(n,m\) 全为偶数时: \(n+m-1\leq k\leq n\times m-1\)
其它情况时: \(n+m-2\leq k\leq n\times m-1\)
下面考虑如何构造答案
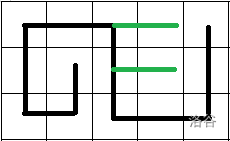
根据每一个 \(k\) ,我们可以先构造出下界,然后一点点加线,而延长直径的方式就是从两端不断延伸,回形般的想中间延伸,知道达到直径长度即可
图示:
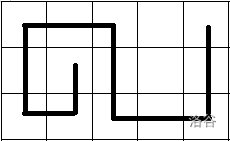
对于剩下的未连接的格点,为了不使得直径延长,可以使每个格点都直接连上一个不是端点的且已在线上的点,如下图所示(绿色的边):
时间复杂度 \(O(nm+k)\)