《LGJOJ 8.23》 测试总结
\(T1\) 益智小游戏



首先我们可以想到的是暴力 \(dfs\) ,这个是没有问题的。
但是这样时间复杂度是有问题的,一个位置至多是可以有 \(600\) 个答案(听别人说的,不知道对不对,反正就是很多),然后再乘一个 \(nm\) 显然爆炸。
然后我们就思考 \(dp\) 怎么做。
我们考虑以行为阶段,记状态 \(dp_{i,j,q}\) ,表示在走到第 \(i\) 个位置,第 \(j\) 个位置,走了 \(q\) 步的方案数。
但是我们不能往上走,不然就有后效性了,考虑只能往下、左、右走,对于往上走的我们再直接计算。
于是我们就有了一个看上去好像可以的做法,但是实际上因为我们不能走到重复的位置,所以我们就得记录上一行以及自己这一行走过的格子的信息,但是无论怎么记录都是难以通过,因为要分太多情况,以及太多信息了。
但是如果可以记录实际上我们这题就可以做了。
我们考虑如何使得我们不用记录那么多信息。
于是我们就可以考虑容斥,先随便走,然后再将走到重复的位置给减掉,这样我们就不用记录太多信息了。
现在我们考虑什么时候会走到重复的位置。
发现当只有走到第 \(5,6\) 步时,才有可能会走到重复位置。
考虑第 \(5\) 步怎么重复的。
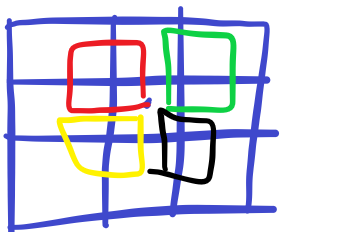
对于这张图,我们中间的格子可以走四种路径回到自己,其中每种路径都有两个方向,第 \(5\) 步时我们减掉走回自己的。
再考虑第 \(6\) 步。
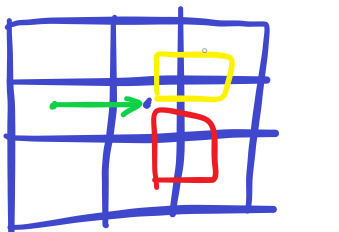
假如我们从绿色的点走过来,然后到蓝色的点,那么我们蓝色的点如何走回自己(不能走到绿色的点,那样就算重复了,因为在第 \(5\) 步的时候,走回绿色的情况已经被减掉了,不能再考虑走到绿色的情况) ,那么我们有走两边两个矩形的方案数。
然后我们的起始点还有四个方向,四个方向都容斥一下就可以了。
总结:
如果我们为了计算恰好的贡献而导致要记录很多信息时,可以考虑容斥,这样往往不需要记录太多信息。
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=3010;
int n,m,k;
LL ans;
char ch[MAXN][MAXN];
bool sf[MAXN][MAXN];
int sum[MAXN][MAXN],f[MAXN][MAXN][5],g[MAXN][MAXN][5],ls[MAXN][MAXN];
int dx[10+10]={0,0,1,-1};
int dy[10+10]={1,-1,0,0};
int qh(int x,int y,int xx,int yy) {
if(x<1||xx<1||y<1||yy<1||x>n||xx>n||y>m||yy>m) return 114514;
return sum[xx][yy]-sum[xx][y-1]-sum[x-1][yy]+sum[x-1][y-1];
}
int main () {
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;++i) {
for(int j=1;j<=m;++j) {
ch[i][j]=getchar();
while(ch[i][j]!='.'&&ch[i][j]!='#') ch[i][j]=getchar();
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+(ch[i][j]=='#');
}
}
for(int i=1;i<=n;++i) {
for(int j=1;j<=m;++j) {
if(ch[i][j]=='#') continue;
f[i][j][4]=1;
}
}
for(int i=2;i<=k;++i) {
for(int j=1;j<=n;++j) {
for(int q=1;q<=m;++q) {
ls[j][q]=0;
for(int w=0;w<=4;++w) {
g[j][q][w]=f[j][q][w];
f[j][q][w]=0;
ls[j][q]+=g[j][q][w];
}
}
}
for(int j=1;j<=n;++j) {
for(int q=1;q<=m;++q) {
if(ch[j][q]=='#') continue;
for(int w=0;w<4;++w) {
int xx=j+dx[w];
int yy=q+dy[w];
f[j][q][w]+=ls[xx][yy]-g[xx][yy][w^1];
}
}
}
if(i==5) {
for(int j=1;j<=n;++j) {
for(int q=1;q<=m;++q) {
if(!qh(j,q,j+1,q+1)) --f[j][q][2],--f[j][q][0];
if(!qh(j-1,q,j,q+1)) --f[j][q][0],--f[j][q][3];
if(!qh(j-1,q-1,j,q)) --f[j][q][3],--f[j][q][1];
if(!qh(j,q-1,j+1,q)) --f[j][q][1],--f[j][q][2];
}
}
}
if(i==6) {
for(int j=1;j<=n;++j) {
for(int q=1;q<=m;++q) {
int ls=0;
if(!qh(j,q,j+1,q+1)) {
ls=(ch[j-1][q]=='.')+(ch[j][q-1]=='.');
// cout<<ls<<' ';
f[j][q][2]-=ls,f[j][q][0]-=ls;
}
if(!qh(j-1,q,j,q+1)) {
ls=(ch[j][q-1]=='.')+(ch[j+1][q]=='.');
// cout<<ls<<' ';
f[j][q][0]-=ls,f[j][q][3]-=ls;
}
if(!qh(j-1,q-1,j,q)) {
ls=(ch[j][q+1]=='.')+(ch[j+1][q]=='.');
// cout<<ls<<' ';
f[j][q][3]-=ls,f[j][q][1]-=ls;
}
if(!qh(j,q-1,j+1,q)) {
ls=(ch[j-1][q]=='.')+(ch[j][q+1]=='.');
// cout<<ls<<' ';
f[j][q][1]-=ls,f[j][q][2]-=ls;
}
}
}
}
// for(int j=1;j<=n;++j) {
// for(int q=1;q<=m;++q) {
// int lll=0;
// for(int w=0;w<4;++w) {
// lll+=f[j][q][w];
// }
// printf("%d ",lll);
// }
// puts("");
// }
// puts("");
}
for(int i=1;i<=n;++i) {
for(int j=1;j<=m;++j) {
for(int q=0;q<5;++q) {
ans=(ans+f[i][j][q]);
}
}
}
printf("%lld\n",ans);
return 0;
}
\(T2\) \(LCA\) 问题




首先有一个比较难想到的性质.
换根是假的,如果现在的根是 \(rt\) ,要求此时 \(x,y\) 的 \(lca\) ,那么其实他们的 \(lca\) 就是 \(LCA(rt,x)\oplus LCA(rt,y) \oplus LCA(x,y)\)
那么我们的问题就变成了 \(LCA(rt,l_1\sim r_1)\oplus LCA(rt,l_2\sim r_2)\oplus LCA(l_1\sim r_1,l_2\sim r_2)\)
所以我们现在的关键就是如何维护区间 \(LCA\)
这个东西数据结构比较难以维护。
我们考虑最直接的暴力分块,设块长为 \(B\) 。
我们处理一个 \(f_{i,j}\) 表示第 \(i\) 个数与第前 \(j\) 个块中的数的 \(lca\) 的异或。
那么实际上我们如果换根 \(dp\) ,从 \(u\to v\) ,那么就看一下 \(v\) 子树中第 \(j\) 个块的节点数量是否为奇数,如果是,就 \(\oplus u\oplus v\)
然后我们就可以在 \(\frac {n^2}B\) 的时间复杂度求出 \(f\) 数组了。
然后再求一个 \(g_{i,j}\)
表示前 \(i\) 个数 与前 \(j\) 个块的 \(lca\) 异或。
对于回答询问,分成散对散,散对整,整对整。
散对散直接暴力,散对整用 \(g\) 就好了,整对整同理。
对于每个询问,需要 \(B^2\) 的时间复杂度,回答询问的总时间复杂度就是 \(qB^2\)
总时间复杂度就是 \(O(\frac {n^2}B+qB^2)\) 平衡一下复杂度,\(B\) 取 \(n^{\frac 23}\) 时,时间复杂度最优 \(O(n^{\frac 53})\) ,\(n,q\) 同阶。
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=5e4+10,NN=1300;
int n,Q,B;
int id[MAXN];
int L[NN],R[NN],len[NN];
int sz[MAXN][NN];
int f[MAXN][NN];
vector<int> e[MAXN];
void add(int f,int t) {
e[f].push_back(t);
e[t].push_back(f);
}
void dfs(int node,int fa) {
sz[node][id[node]]=1;
for(auto t:e[node]) {
if(t==fa) continue;
dfs(t,node);
for(int i=1;i<=id[n];++i) {
sz[node][i]+=sz[t][i];
}
}
}
void dfs1(int node,int fa) {
for(auto t:e[node]) {
if(t==fa) continue;
for(int i=1;i<=id[n];++i) {
if(sz[t][i]%2) f[t][i]=f[node][i]^node^t;
else f[t][i]=f[node][i];
}
dfs1(t,node);
}
}
void ycl_f() {
scanf("%d%d",&n,&Q);
B=67;
for(int i=1;i<n;++i) {
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;++i) {
id[i]=(i-1)/B+1;
}
for(int i=1;i<=id[n];++i) {
L[i]=(i-1)*B+1;
R[i]=min(i*B,n);
len[i]=R[i]-L[i]+1;
}
// cout<<R[2]<<' '<<R[3]<<endl;
for(int i=1;i<=id[n];++i) {
f[1][i]=len[i]%2;
}
dfs(1,0);
dfs1(1,0);
// cout<<f[1][1]<<' ';
}
int g[MAXN][NN];
void ycl_g() {
for(int i=1;i<=id[n];++i) {
for(int j=1;j<=n;++j) {
f[j][i]=f[j][i]^f[j-1][i];
}
}
for(int i=1;i<=id[n];++i) {
for(int j=1;j<=n;++j) {
g[j][i]=g[j][i-1]^f[j][i];
}
}
}
int xl[MAXN*2],in[MAXN],cnt;
int logg[MAXN*2],st[20][MAXN*2];
void DFS(int node,int fa) {
xl[++cnt]=fa;
in[node]=cnt;
for(auto t:e[node]) {
if(t==fa) continue;
DFS(t,node);
}
}
int get(int x,int y) {
if(in[x]<in[y]) return x;
return y;
}
void ycl_st() {
DFS(1,0);
for(int i=2;i<=cnt;++i) logg[i]=logg[i/2]+1;
for(int i=1;i<=cnt;++i) {
st[0][i]=xl[i];
}
for(int i=1;i<=logg[cnt];++i) {
int R=cnt-(1<<i)+1;
for(int j=1;j<=R;++j) {
int t=st[i-1][j+(1<<(i-1))];
st[i][j]=get(st[i-1][j],st[i-1][j+(1<<(i-1))]);
}
}
}
int query(int x,int y) {
if(x==y) return x;
x=in[x]; y=in[y];
if(x>y) swap(x,y);
++x;
int k=logg[y-x+1];
return get(st[k][x],st[k][y-(1<<k)+1]);
}
int ans;
void solve(int p,int x,int y) {
int ls1=id[x]-1,ls2=id[y]-1,anss=ans,rr=R[ls1];
ans^=g[y][ls1];
ans^=g[x][ls2]^g[rr][ls2];
anss=ans;
for(int i=L[id[x]];i<=x;++i) {
for(int j=L[id[y]];j<=y;++j) {
ans^=query(i,j);
}
} //散散
anss=ans;
if(y&1) {
ans^=g[p][ls1]^g[p-1][ls1];
for(int j=L[id[x]];j<=x;++j) {
ans^=query(p,j);
}
}
if(x&1) {
ans^=g[p][ls2]^g[p-1][ls2];
for(int j=L[id[y]];j<=y;++j) {
ans^=query(p,j);
}
}
}
int main () {
ycl_f();
ycl_g();
ycl_st();
for(int i=1;i<=Q;++i) {
int rt,l1,r1,l2,r2; ans=0;
scanf("%d%d%d%d%d",&rt,&l1,&r1,&l2,&r2);
solve(rt,r1,r2);
solve(rt,l1-1,r2);
solve(rt,r1,l2-1);
solve(rt,l1-1,l2-1);
printf("%d\n",ans);
}
return 0;
}
\(T3\) 区间



简直和前天的 \(t1\) 一模一样
只需要对于每个 \(D\) 分开来处理即可。
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=1e5+10,NN=1e6+10;
int n,m,DADA;
int a[MAXN];
struct ddl{
int x,i;
}l[110];
struct daduoli {
int st,l,r;
};
bool cmp(daduoli a,daduoli b) {
return a.st<b.st;
}
vector<daduoli> e[NN];
int gcd(int x,int y) {
return (!y?x:gcd(y,x%y));
}
LL ans[MAXN];
struct ask {
int x,l,r,opt,id;
};
bool cmp1(ask a,ask b) {
return a.x<b.x;
}
vector<ask> E[NN];
void ycl() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) {
scanf("%d",&a[i]); DADA=max(DADA,a[i]);
}
int cnt=0;
for(int i=n;i>=1;--i) {
l[++cnt].x=a[i]; l[cnt].i=i;
for(int j=cnt;j>=1;--j) {
l[j].x=gcd(l[j].x,a[i]);
}
int ls=0;
for(int j=1;j<=cnt;++j) {
if(l[j].x!=l[j-1].x) {
l[++ls]=l[j];
}
}
cnt=ls;
for(int j=1;j<=cnt;++j) {
if(j<cnt) {
e[l[j].x].push_back((daduoli){i,l[j+1].i+1,l[j].i});
// cout<<l[j+1].i+1<<' '<<l[j].i<<endl;
}
else e[l[j].x].push_back((daduoli){i,i,l[j].i});
// cout<<l[j].x<<" "<<l[j].i<<endl;
}
// puts("");
}
for(int i=1;i<=m;++i) {
int l,r,d;
scanf("%d%d%d",&l,&r,&d);
E[d].push_back((ask){l-1,l,r,-1,i});
E[d].push_back((ask){r,l,r,1,i});
}
}
struct ds {
LL zz,s,lb;
}tr[MAXN*4];
void add(int node,int z,int l,int r) {
tr[node].lb+=z;
tr[node].s+=z*(r-l+1);
}
void clear(int node) {
tr[node].lb=tr[node].s=0;
tr[node].zz=1;
}
void psdn(int node,int l,int mid,int r) {
if(tr[node].zz) {
clear((node<<1));
clear((node<<1|1));
tr[node].zz=0;
}
if(tr[node].lb) {
add((node<<1),tr[node].lb,l,mid);
add((node<<1|1),tr[node].lb,mid+1,r);
tr[node].lb=0;
}
}
void psup(int node) {
tr[node].s=(tr[(node<<1)].s+tr[(node<<1|1)].s);
}
void update(int node,int l,int r,int x,int y) {
if(l>y||r<x) return ;
if(l>=x&&r<=y) {
add(node,1,l,r);
return ;
}
int mid=(l+r)/2;
psdn(node,l,mid,r);
update((node<<1),l,mid,x,y);
update((node<<1|1),mid+1,r,x,y);
psup(node);
}
LL query(int node,int l,int r,int x,int y) {
if(l>y||r<x) return 0;
if(l>=x&&r<=y) return tr[node].s;
int mid=(l+r)/2;
psdn(node,l,mid,r);
return (query((node<<1),l,mid,x,y)+query((node<<1|1),mid+1,r,x,y));
}
void cl() {
for(int i=1;i<=DADA;++i) {
sort(e[i].begin(),e[i].end(),cmp);
sort(E[i].begin(),E[i].end(),cmp1);
int l1=0,l2=0,len1=e[i].size(),len2=E[i].size();
tr[1].zz=1;
while(l1<len1&&l2<len2) {
if(e[i][l1].st<=E[i][l2].x) update(1,1,n,e[i][l1].l,e[i][l1].r),++l1;
else ans[E[i][l2].id]+=E[i][l2].opt*query(1,1,n,E[i][l2].l,E[i][l2].r),++l2;
}
while(l2<len2) {
ans[E[i][l2].id]+=E[i][l2].opt*query(1,1,n,E[i][l2].l,E[i][l2].r);
++l2;
}
}
}
void prin() {
for(int i=1;i<=m;++i) {
printf("%lld\n",ans[i]);
}
}
int main () {
ycl();
cl();
prin();
return 0;
}
\(T4\) 平衡网络




首先可以很容易想到对于每个不同的质数我们可以分开来处理(我没想到)
然后一个 \(a_{i,j}\) 拆成 \(x,y\)
我们可以看成 \(X_i\) 乘上了 \(\frac xy\) ,\(X_j\) 乘上了 \(\frac yx\)
然后我们只对与一个质数考虑先,因为会了一个质数的,对于所有质数也就会了。
我们只需要考虑他的次数,将 \(x,y\) 对于以一个质数为底,他的次数分别记为 \(c,d\) ,也就是说 \(X_i\) 加上了 \((c-d)\) , \(X_j\) 加上了 \(d-c\)
也就是说我们最后要使所有 \(X\) 均为 \(0\)
我们可以把对于 \(a_{i,j}\) 有多少次数,我们可以看成 \(i,j\) 之间连多少条无向边,倘若从 \(i\) 走到 \(j\) ,就相当于 \(j+1\) ,\(i-1\) ,最后我们要使所有数收支平衡,就是入度等于出度,就相当于跑一遍欧拉回路。
时间复杂度 \(O(nm\sqrt V)\)
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=110,NN=1e6+10;
int n;
int a[MAXN][MAXN];
int ans[MAXN][MAXN],in[MAXN],out[MAXN];
struct ddl {
int f,t,c;
};
vector<ddl> e[NN];
vector<int> ee[NN];
bool sf[NN];
struct daduoli {
int f,t,c,F,T;
}que[MAXN*MAXN*2];
int cnt,h[MAXN],ind[MAXN*MAXN*22];
void add(int f,int t,int c,int F,int T) {
que[++cnt].f=h[f];
que[cnt].t=t;
que[cnt].c=c;
que[cnt].F=F;
que[cnt].T=T;
h[f]=cnt;
}
int res,tot;
void dfs(int node,int p,int pp) {
for(int i=h[node];i;i=h[node]=que[i].f) {
while(que[i].c>0) {
--que[i].c;
--que[(i^1)].c;
dfs(que[i].t,que[i].F,que[i].T);
}
}
ind[++tot]=node;
if(node==p) ans[p][pp]=ans[p][pp]*res;
}
int main () {
scanf("%d",&n);
for(int i=1;i<=n;++i) {
for(int j=1;j<=n;++j) {
ans[i][j]=1;
scanf("%d",&a[i][j]);
if(i==j) continue;
int r=sqrt(a[i][j]);
int x=a[i][j];
for(int q=2;q<=r;++q) {
if(x%q==0) {
ee[q].push_back(i);
ee[q].push_back(j);
sf[q]=1;
int cnt=0;
while(x%q==0) {
++cnt;
x/=q;
}
e[q].push_back((ddl){i,j,cnt});
}
}
if(x!=1) {
sf[x]=1;
ee[x].push_back(i);
ee[x].push_back(j);
e[x].push_back((ddl){i,j,1});
}
}
}
for(int i=1;i<=NN-10;++i) {
res=i;
if(!sf[i]) continue;
int len=ee[i].size();
for(int j=0;j<len;++j) {
in[ee[i][j]]=0; out[ee[i][j]]=0; h[ee[i][j]]=0;
} cnt=1;
for(auto t:e[i]) {
add(t.f,t.t,t.c,t.f,t.t);
add(t.t,t.f,t.c,t.f,t.t);
}
for(int j=0;j<len;++j) {
tot=0;
dfs(ee[i][j],0,0);
for(int q=tot;q>1;--q) {
++out[ind[q]];
++in[ind[q-1]];
}
}
for(int j=0;j<len;++j) {
if(in[ee[i][j]]!=out[ee[i][j]]) {
puts("NO");
return 0;
}
}
}
puts("YES");
for(int i=1;i<=n;++i) {
for(int j=1;j<=n;++j) {
printf("%d ",ans[i][j]);
}
puts("");
}
return 0;
}