P7886 Gerrymandering
简单的构造题。
给定正整数 \(n,m,k\) 能否将一个 \(n\times m\) 表格染色,使得每一个颜色形成恰好一个连通块,并且每一个连通块大小为 \(k\)。如果存在,构造一个合法方案。
对于矩形涂色,使其形成连通块一个,一个常见思路是走蛇形路线:从第一行左端开始涂色,走到行末跳到下一行反向涂,涂 \(k\) 个格子换色。如果 \(n\times m\) 能被 \(k\) 整除,则可以完成涂色。具体如下图所示:
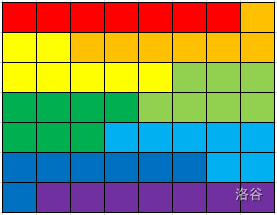
所以,对于样例4 3 2而言,我们涂色结果是这样的:
1 1 2
3 3 2
4 4 5
6 6 5
需要注意一个细节,\(\sum n\times m \le 10^6\),所以不能直接开二维数组(MLE),可以开一个一维的 \(10^6\) 的数组,只存当前行的颜色。