缩点传送门

根据题意：允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

所以我们可以考虑将可以相互到达的若干个点缩成一个点，以方便计算。

下面讲如何实现：

考虑\(dfs\)，并且对点记录如下信息\(dfn\)（该点被遍历到的时间节点，即该点是第几个被遍历到的），\(low\)（可以追溯到的最小的时间节点，即可以到达的点中最小的\(dfn\)）。

考虑遍历到\(u\)时：

记录当前的\(dfn_u\)和\(low_u\)，均为\(++times\)，即当前可以追溯到的最小的时间节点为当前的时间节点（\(times\)仅仅是记录一下当前被遍历到的点的个数）

考虑一条\(u->v\)的有向边

1、若\(v\)之前没有被遍历到：开始遍历\(v\)，遍历完\(v\)后，更新\(low_u=min(low_u,low_v)\)，即比较\(low_v\)可以追溯到的最小的时间节点是否比\(low_u\)小，小则更换，毕竟\(u\)可以到\(v\)

2、若\(v\)之前有被遍历到且可以到达\(u\) ：则更新\(low_u=min(low_u,low_v)\)

注意：这里要\(v\)可以到达\(u\)，因为如果\(v\)不可以到达\(u\)，则\(u,v\)之间不可以缩点，而\(low\)时判断是否可以缩点的一个值，所以这里要有这个条件，第一步中之所以不用判断是因为若\(u\)无法连\(v\)，那么\(low_v>low_u\)，\(low_v\)什么也改变不了，但第二步中\(low_v\)有可能比\(low_u\)小，只是到不了\(u\)而已，所以如果不判断会导致答案错误（判断\(v\)是否可以到达\(u\)在代码中用\(vis\)实现）

3、以上均不是，则什么都不操作

考虑\(u\)点可以缩点：

\(low_u=dfn_u\)，表示这个点是最早被遍历到的，后面可以与这个点相互到达的点\(v\)必然会有\(low_v<dfn_v\)，而他们都将被缩成一个点，即\(u\)

考虑缩完点后做什么：

假设缩完点后的点为\(d_1,d_2...,d_k\)，缩点的点值为该点所包含的所有点的点值，分别为\(s_1,s_2,...,s_k\)

枚举边。

考虑有向边\(u->v\)

如果\(u\)所在的缩点与\(v\)所在的缩点不同，那么\(u\)所在的缩点可以到达\(v\)所在的缩点，然后连一条\(u\)所在的缩点到\(v\)所在的缩点的边

拓扑排序\(+DP\)

对于拓扑到的缩点\(d_v\)，可以到达它的点必然已经被计算过，那么以它为结尾的最大点权和为\(\max\limits_{d_u->d_v}(f_u+s_v)\)

上代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N=100010,M=500010;
ll n,m,a[N],u,v;
struct jgt
{
	ll from,to,ne;
}edge[M];
ll h[N],idx;
void add(ll x,ll y)
{
	edge[idx].from=x;
	edge[idx].to=y;
	edge[idx].ne=h[x];
	h[x]=idx++;
}
ll dfn[N],low[N],times,sta[N],in,tot,bh[N],dian[N];
bool vis[N];
ll rd[N];
vector<ll> cb[N];
vector<ll> rb[N];
ll ans[N],cnt;
ll f[N];
void tuopu()
{
	queue<ll> q;
	for(ll i=1;i<=tot;i++)
	{
		if(rd[i]==0) q.push(i);
	}
	while(!q.empty())
	{
		ll now=q.front();
		q.pop();
		ans[++cnt]=now;
		for(ll i=0;i<cb[now].size();i++)
		{
			ll j=cb[now][i];
			rd[j]--;
			if(rd[j]==0) q.push(j);
		}
	}
}
void tarjan(ll x)
{
	dfn[x]=low[x]=++times;
	sta[++in]=x;
	vis[x]=true;
	for(ll i=h[x];i!=-1;i=edge[i].ne)
	{
		if(!dfn[edge[i].to])
		{
			tarjan(edge[i].to);
			low[x]=min(low[x],low[edge[i].to]);
		}
		else if(vis[edge[i].to]) low[x]=min(low[x],low[edge[i].to]);
	}
	if(low[x]==dfn[x])
	{
		tot++;
		while(1)
		{
			bh[sta[in]]=tot;
			dian[tot]+=a[sta[in]];
			vis[sta[in]]=false;
			in--;
			if(x==sta[in+1]) break;
		}
	}
}
int main()
{
	memset(h,-1,sizeof h);
	scanf("%lld %lld",&n,&m);
	for(ll i=1;i<=n;i++)
	scanf("%lld",&a[i]);
	for(ll i=1;i<=m;i++)
	{
		scanf("%lld %lld",&u,&v);
		add(u,v);
	}
	for(ll i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
	for(ll i=0;i<idx;i++)
	{
		if(bh[edge[i].from]!=bh[edge[i].to])
		{
			u=bh[edge[i].from],v=bh[edge[i].to];
			rd[v]++;
			cb[u].push_back(v);
			rb[v].push_back(u);
		}
	}
	tuopu();
	for(ll i=1;i<=tot;i++)
	{
		ll w=ans[i];
		f[w]=dian[w];
		for(ll j=0;j<rb[w].size();j++)
		f[w]=max(f[w],f[rb[w][j]]+dian[w]);
	}
	ll sum=0;
	for(ll i=1;i<=tot;i++)
	sum=max(sum,f[i]);
	printf("%lld\n",sum);
	return 0;
}

割点传送门

割点定义（感性理解）：对于一个无向连通图，去掉一个点及有关该点的连边后，这一个无向连通图变成了两个无向连通图，这个点就称为改图的割点。

之所以合在一起讲，是因为判断割点的操作也差不多

然后我们就可以复制了

考虑\(dfs\)，并且对点记录如下信息\(dfn\)（该点被遍历到的时间节点，即该点是第几个被遍历到的），\(low\)（可以追溯到的最小的时间节点，即可以到达的点中最小的\(dfn\)），\(son\)（该点有多少个儿子）。

考虑遍历到\(u\)时：

记录当前的\(dfn_u\)和\(low_u\)，均为\(++times\)，即当前可以追溯到的最小的时间节点为当前的时间节点（\(times\)仅仅是记录一下当前被遍历到的点的个数）

考虑一条\(u--v\)的无向边（遍历\(u\)所连的边时遍历到\(v\)）

1、若\(v\)之前没有被遍历到：令\(son_u++\)，表示\(u\)多了一个儿子，开始遍历\(v\)，遍历完\(v\)后，更新\(low_u=min(low_u,low_v)\)，即比较\(low_v\)可以追溯到的最小的时间节点是否比\(low_u\)小，小则更换，毕竟\(u\)可以到\(v\)

然后与缩点不同的是，若\(low_v>=dfn_u\)且\(u!=root\)，则该点是割点，因为\(v\)无法不通过\(u\)到达其他\(dfn\)小于\(u\)的点

2、若\(v\)之前有被遍历到：则更新\(low_u=min(low_u,dfn_v)\)

注意：是\(dfn_v\)，原因是它是前面已经遍历过的点，当回溯到\(v\)时，会判断\(u\)能否做到不通过\(v\)到达前面已经遍历过的点，即\(dfn\)小于\(dfn_v\)的点，若是\(low_v\)，则会是通过\(v\)到达已遍历的点，造成答案错误。

如图所示：

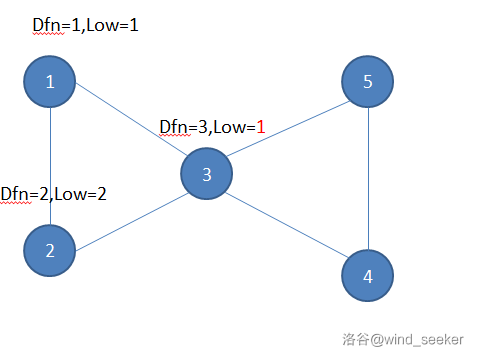
理解程序如何判断点\(u\)是否为割点：

若\(u!=root\)，看看除掉该点后，未遍历的点是否能到达已遍历的点

若\(u==root\)，则看他是否有大于等于两个儿子

上代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N=1e5+50;
ll n,m,u,v,root;
vector<ll> e[N];
ll dfn[N],low[N],idx,cnt,buc[N];
void dfs(ll wz)
{
	dfn[wz]=low[wz]=++idx;
	ll son=0;
	for(ll i=0;i<e[wz].size();i++)
	{
		ll j=e[wz][i];
		if(!dfn[j])
		{
			son++;
			dfs(j);
			low[wz]=min(low[wz],low[j]);
			if(low[j]>=dfn[wz]&&wz!=root) cnt+=!buc[wz],buc[wz]=1;
		}
		else low[wz]=min(low[wz],dfn[j]);
	}
	if(son>=2&&wz==root) cnt+=!buc[wz],buc[wz]=1;
}
int main()
{
	scanf("%lld %lld",&n,&m);
	for(ll i=1;i<=m;i++)
	{
		scanf("%lld %lld",&u,&v);
		e[u].push_back(v);
		e[v].push_back(u);
	}
	for(ll i=1;i<=n;i++) if(!dfn[i]) root=i,dfs(i);
	printf("%lld\n",cnt);
	for(ll i=1;i<=n;i++) if(buc[i]) printf("%lld ",i);
	return 0;
}