T1 三值的排序

对于一个给定的只由 \(1,2,3\)数字序列,请计算排成升序所需的最小交换次数

【数据范围】

对于 \(100\%\) 的数据, \(1\leq n\leq1000\)

题解

由于序列只由 \(1,2,3\) 组成,可能的错位情况很少,顾可先排序然后通过错位数字的位置情况再分类讨论:

举个栗子

• 原序列: \(2,2,1,3,3,3,2,3,1\)

• 排序后: \(1,1,2,2,2,3,3,3,3\)

首先考虑只涉及到两个数字之间的错位情况,则有 \(a_i=2,a_j=1(i<j)\) 和\(a_i=3,a_j=2(i<j)\)这两种,这两种之间相互独立,顾可分开处理,每一次交换将会增加 \(1\) 的贡献(情况 \(1\) )

然后就是三个数字错位的情况,当 \(1,2,3\) 同时错位时,每次交换将增加 \(2\) 的贡献(情况 \(2\) )

故最终答案为 情况 \(1+\) 情况 \(2\times 2\)

时间复杂度为 \(O(nlogn)\)

备注:一个无序序列若只允许交换相邻的两个元素,则整个序列的交换次数为这个序列里的逆序对的个数

T2 日记

给定 \(T\) 组数据,每组给定 \(N,k\)，询问不超过 \(N\) 的数中能够表示成连续的 \(k\) 个质数之和的最大的数是多少,不存在请输出 \(-1\)

一定注意无解时的输出条件(痛挂 \(60\) pts)

【数据范围】

\(1\leq N \leq 10^6,0 \leq k \leq 10^9\)

题解

欧拉筛预处理 \(10^6\) 以内的质数,做一遍前缀和,然后二分枚举答案区间的右端点即可

时间复杂度为 \(O(TlogN)\)

T3 分蛋糕

蛋糕是圆形的，从蛋糕中某点开始将蛋糕放射状切为 \(N\) 块，按逆时针顺序编号为 \(1\) 到 \(N\) 。切了之后的第 \(i\) 块蛋糕的大小为 \(A_i\) 。由于切蛋糕的人刀功很不好，所以 \(A_i\) 互不相同。

示例图片:

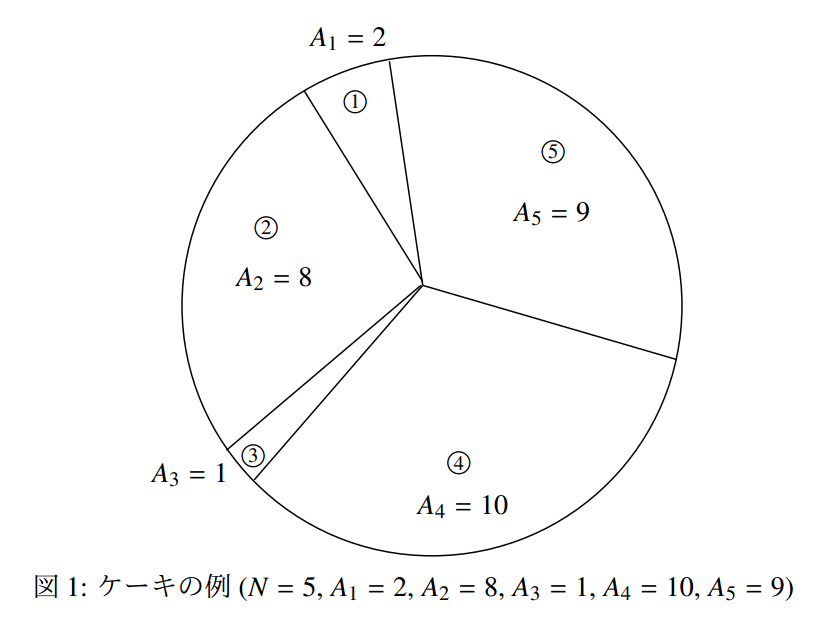
小 \(Y\) 和 小 \(Z\) 按照以下方法分这 \(N\) 块蛋糕：

1. 首先 小 \(Y\) 从这 \(N\) 块蛋糕中任选一块取走；
2. 然后，从 小 \(Z\) 开始，小 \(Z\) 和 小 \(Y\) 交替地从剩下的蛋糕中选出一块取走。不过，当且仅当一块蛋糕两旁的蛋糕至少有一块已经被选择，这块蛋糕才能被选择。如果可供选择的蛋糕有多个，小 \(Z\) 会选择最大的一个，而 小 \(Y\) 可以任选一个。
   小 \(Y\) 想让自己所得到的蛋糕大小的合计值最大。

给出蛋糕的块数 \(N\) 和这 \(N\) 块蛋糕的大小。请编写程序求出小 \(Y\) 得到的蛋糕大小的总和的最大值。

【数据范围】

\(1 \leq N \leq 2000,1 \leq A_i \leq 10^9\)

题解

比较经典的区间DP+记忆化搜索的题目

对于环上问题,首先考虑复制一倍

状态设计:设 \(dp_{l,r}\) 表示选择区间 \(l \sim r\) 可以获得的最大价值和

状态转移:

设当前枚举的区间为 \(l \sim r\) ,每块蛋糕的贡献为 \(v_i\)

• 当选择左端点 \(l\) 时,剩余可选区间为 \(l+1 \sim r\)
  • 若 \(v_{l+1}<v_r\),则 $dp_{l,r}=\max\left(dp_{l,r},v_l+dp_{l+2,r}\right) $(小 \(Z\) 会选两个边界里最大的)
  • 若 \(v_{l+1}>v_r\),则 \(dp_{l,r}=\max \left(dp_{l,r},v_r+dp_{l+1,r-1}\right)\)
• 当选择右端点 \(r\) 时,剩余可选区间为 \(l\sim r-1\)
  • 若 \(v_l<v_{r-1}\),则 \(dp_{l,r}=\max\left(dp_{l,r},v_r+dp_{l,r-2}\right)\)
  • 若 \(v_l>v_{r-1}\),则 \(dp_{l,r}=\max \left(dp_{l,r},v_r+dp_{l+1,r-1}\right)\)

递归边界:

• 当 \(l=r\) 时,返回 \(v_l\)

• 当 \(l+1=r\) 时,返回 \(\max\left(v_l,v_r\right)\)

• 当 \(dp_{l,r}>0\) 时,返回 \(dp_{l,r}\)

总状态数为 \(n^2\),每次循环枚举断点即可

时间复杂度为 \(O(n^3)\)

T4 都市

有 \(N\) 个数,但不给你，而是给了你 \(N \times (N-1)/2\) 个数，代表它们两两的和。那么这 \(N\) 个数的所有可能解

【数据范围】

\(1 \leq N \leq 300,N\) 个数均不超过 \(10^8\) 且均为正整数

题解

我们设 \(a_i\) 表示一组可能解中的第 \(i\) 个数字,设 \(a\) 为有序序列

则有 \(a_1<a_2<a_3 \cdots <a_{n-1}<a_n\)

将读入的所有数字排序后,不难发现 \(a_1+a_2\) 一定是最小的那一个, \(a_1+a_3\) 是次小的,但 \(a_2+a_3\) 大小不定,需要枚举

那么可以通过上述的三个值来确定前三个数字并删去这三个数字所对应的值

可以发现当前序列最小的是 \(a_1+a_4\) ,那么我们可以确定 \(a_4\) 并删除 \(a_1+a_4,a_2+a_4,a_3+a_4\)

以此类推,我们可以每次确定一个数字就删去不大于它的确定数字和他所对应的和,若无无法找到则可判为无解,直到最后找出一组可行解,若在操作中遇到无解或找到一组可行解的时候,需要及时还原序列以进行下一次的操作,用 \(multiset\) 维护即可

时间复杂度约为 \(O(N^3)\) ,但实际根本跑不满

T5街灯

街上一共有 \(N\) 个街灯,每个街灯上都有一个数,有 \(M\) 次询问,每次询问，第 \(l\) 个街灯到 第 \(r\) 个街灯上的数模 \(p\) 等于 \(v\) 的有几个？

【数据范围】

\(1 \leq N,M \leq 10^5\) ,街灯上的数不超过 \(10^4\) , \(1 \leq p \leq 10^9\)

题解

根号分治模板题

首先开一个 \(vector~vec\) ,其中 \(vec_{i,j}\) 表示在对 \(i\) 取模的前提下结果为 \(j\) 的数字集合

读入数据的时候，对于每个数预处理模数为 \(100\) 以内的结果并将当前数字存储到对应的 \(vec\) 数组里,并同时开一个记录每个数值所对应的下标的 \(vector\) 集合,对于小于 \(100\) 以内的模数 \(p\) 直接查询,而大于 \(100\) 的数字则计算在询问区间内的为 \(v+xp\) 形式的数字( \(x\) 为系数),二分 \(100\) 次即可

这样可以将原来的 \(10^4\) 均摊成两个 \(10^2\) 的复杂度,对于两边分别处理的做法即为根号分治

时间复杂度 \(O(n \times \sqrt n \times logn)\)