状压 dp 总结[未完待续]

三进制状压

Q&A

1.如果我的当前的dp值需要前两个状态才可以推导出来怎么办?

很简单,既然我们无法舍弃任何一个状态那我们就加一维将它纳入考虑范围之内,就拿 P8756 [蓝桥杯 2021 省 AB2] 国际象棋做列子
我们本列的马最远是可以威胁到前两列的马,那么我们就让 dp 表示这一列与上一列的马的情况,这样子转移就很明了了.

for(int i=1;i<=m;i++)
    for(int L=0;L<=(1<<n)-1;L++)
        for(int S=0;S<=(1<<n)-1;S++)
            for(int T=0;T<=(1<<n)-1;T++)
                dp[i][S][T]= contribution(dp[i-1][L][S]);//contribution()这个状态从上一个状态得到的贡献

值得注意的是这个数组肯定是要滚动的,不然爆空间是一件无疑的事情.
类似这样的题目

P2704	[NOI2001] 炮兵阵地
P8756	[蓝桥杯 2021 省 AB2] 国际象棋

2.如果数值太大我们的状态放不下怎么办?
3.如果要考虑

提出这么多个疑问都是为了引出这道题,因为实在觉得这道题出的太好了.

$P2150 [NOI2015] 寿司晚宴$

[NOI2015] 寿司晚宴

题目描述

为了庆祝 NOI 的成功开幕，主办方为大家准备了一场寿司晚宴。小 G 和小 W 作为参加 NOI 的选手，也被邀请参加了寿司晚宴。

在晚宴上，主办方为大家提供了 $n−1$ 种不同的寿司，编号 $1,2,3,\ldots,n-1$，其中第 $i$ 种寿司的美味度为 $i+1$。（即寿司的美味度为从 $2$ 到 $n$）

现在小 G 和小 W 希望每人选一些寿司种类来品尝，他们规定一种品尝方案为不和谐的当且仅当：小 G 品尝的寿司种类中存在一种美味度为 $x$ 的寿司，小 W 品尝的寿司中存在一种美味度为 $y$ 的寿司，而 $x$ 与 $y$ 不互质。

现在小 G 和小 W 希望统计一共有多少种和谐的品尝寿司的方案（对给定的正整数 $p$ 取模）。注意一个人可以不吃任何寿司。

输入格式

输入文件的第 $1$ 行包含 $2$ 个正整数 $n, p$ 中间用单个空格隔开，表示共有 $n$ 种寿司，最终和谐的方案数要对 $p$ 取模。

输出格式

输出一行包含 $1$ 个整数，表示所求的方案模 $p$ 的结果。

提示

【数据范围】

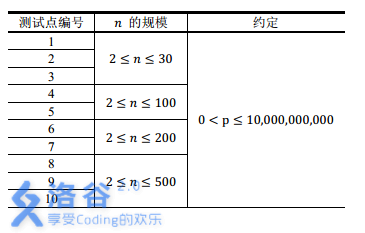
勘误：$0 < p \le 10^9 $

可以从题目中提炼出来的较为浅显的信息:

1.要求全部互质,也就是两人所选的数包括的质因数集合没有交集,可以考虑从这里下手做状态
2.n≤500,我们简单写个输出质因数表的暴力,发现有整整92个质因数,显然直接用来做状态是会爆的

好了,就这些信息了,没了...
大部分选手已经可以根据这些信息得到一个30pts的状压了但我太蒟了
程序实现时盯着自己的草稿纸半天都没有一点动作,看了题解之后还是决定把暴力也详细的推一遍.

我们令n位二进制数表示现在已经包括了x个质因数(有则1无则0),我们先预处理一遍所有数的质因数(把他们转成形如上文的二进制数)
我们对于每一道菜有3种可选的转移:

1.给小G
2.给小W
3.都不给

我们定义dp的第一维表示小G的状态,第二维表示小W的状态

就会有

$$
\begin{cases}

dp[i][G|a[i]][W]+=dp[i-1][G][W] \quad 小G吃了\\
dp[i][G][W|a[i]]+=dp[i-1][G][W] \quad 小W吃了\\
dp[i][G][W]+=dp[i-1][G][W] \quad 都没吃\\

\end{cases}
$$

注意我们这里转移之前都需要先判断会不会 $(G\&a[i])$ 和 $(W\&a[i])$ 都是有值的,也就是说要小心不要让他们吃到有相同质因子的菜啦
暴力告一段落,下面我们开始讲正解,

优化1

我们知道500以内的质因子太多所以会导致我们的状态无法将他们压缩,那么我们就是时候观察一下了 $sqrt(500)\approx 22$,这有什么用呢?这揭示了一个道理,大于22的质因子一个数种最多只会出现一次,这有什么用呢?

我们可以用有区别的决策换取时间和空间

太玄乎了,具体的说,我们可以将小于22小质因子和大于22的大质因子分开来处理(没有大于22的我们就当作是0)
22以内只有8个质因子,这是完全可以压缩的,小质因子这边我们先放着不管
大质因子怎么处理呢?我们考虑将他们按最大的质因子大小排序,这样有相同的大质因子的数就会被聚拢在一起,我们只需要控制让有相同大质因子的数只能被一人选走就好了!

到这里本蒟蒻又开始犯难了,因为这个dp柿子不好写呀,怎么样才能表示一个大因子只被一个人选走了呢?

这就是这道题最妙的地方了,我们可以分两个数组!
$dp1$表示这个数被小G选走了,$dp2$表示这个数被小W选走了
新的dp柿子(猴版):
先
$$
\begin{cases}
dp1[i][G|a[i]][W]+=dp1[i-1][G][W] \quad 小G吃了\
dp2[i][G][W|a[i]]+=dp2[i-1][G][W] \quad 小W吃了\
\end{cases}
$$
再
$$dp[i][G][W]=dp1[i][G][W]+dp2[i][G][W] \quad 总的方案数$$

PS:请不要用这个柿子直接去进行代码的构建,因为它缺失了很多细节,只保留了表义的功能,完整的柿子在后面
看回我们上面暴力推的柿子,有什么区别的地方呢?除了小G与小W的两条方程被劈开来算?
这就是这个操作最妙不可言的地方,只要是连续的大因子数,我们就可以让其中他们互不干扰的连续选菜!这个地方很难直接讲明白,我自己也想的失眠了一个晚上,第二天才看懂.
其实$luogu$的第一篇题解也讲的很详细了,但我实在是太蒟了,我认为这个结合代码流程来看会清晰很多.
一份写满注释的代码

   for (int i = 1; i < n; i++)
    {
        if (i == 1 || big[pt[i]] ^ big[pt[i - 1]] || !big[pt[i]])
        {
            memcpy(dp1, dp, sizeof dp1);//把之前算好的答案copy到dp1,2当中
            memcpy(dp2, dp, sizeof dp2);//其实这里就相当于把不选这个数的贡献统计上,也就是我们暴力柿子中的第三个
        }
        for (int j = 255; j >= 0; j--)
            for (int k = 255; k >= 0; k--)
            {
                int state = x[pt[i]];
                if (j & k)
                    continue;
                if (!(k & x[pt[i]]))//合法性判断
                    (dp1[j | state][k] += dp1[j][k] + p) %= p;
                if (!(j & x[pt[i]]))
                    (dp2[j][k | state] += dp2[j][k] + p) %= p;
            }
        if (i == n - 1 || big[pt[i]] ^ big[pt[i + 1]] || !big[pt[i]])//注意看这里,如果我们没有完成对一类大质因子的贡献计算,那我们就不会统计答案,也不会让统计后的答案copy给dp1与dp2,这样子就保证了同种大质因子不会被两人同时取
        {
            for (int j = 255; j >= 0; j--)
            {
                for (int k = 255; k >= 0; k--)
                {
                    if (j & k)
                        continue;
                    (dp[j][k] = dp1[j][k] + dp2[j][k] - dp[j][k] + p) %= p;
                    // 如果没有大因子那么dp1[j][k]==dp2[j][k]
                    //dp[j][k]之所以要减掉一次自己,是因为在前面它同时把自己赋值给了dp1,dp2,加回来的时候会让原先就有的贡献翻倍,所以要减去一倍
                }
            }
        }
    }

之所以写这么多话是因为别让自己看不懂自己的博客我觉得应该还有很多想我一样dp功底超蒟的同行会在这里苦思冥想没有结果.

优化2

$$dp1[i][G|a[i]][W]+=dp1[i-1][G][W] \quad 小G吃了$$

我们观察一下我们的dp柿子
$$\begin{cases}dp1[i][G|a[i]][W]+=dp1[i-1][G][W] \quad 小G吃了\
dp2[i][G][W|a[i]]+=dp2[i-1][G][W] \quad 小W吃了\ \end{cases}$$
我们可以看到,我们两个柿子都是通过刷表法 (好nb的名字) 得到的,这有什么特别的呢,都是从数值比较小的状态贡献到数值比较大的状态,这个时候我们只需要倒序枚举,保证所有状态的前置状态都不会被提前刷新,一个滚动数组就完成了.
对你没有看错,自动滚动的滚动数组
其实是比较类似于背包的覆盖式滚动,但是又有点别致的地方.

一道好的题真的能让人学到很多东西啊