CSP模拟-30D
[AGC019F] Yes or No
我们可以试着把所有"最优策略的答题历程"放在一张网状图里。
就像这样。(声明:我们默认\(n \geq m\))
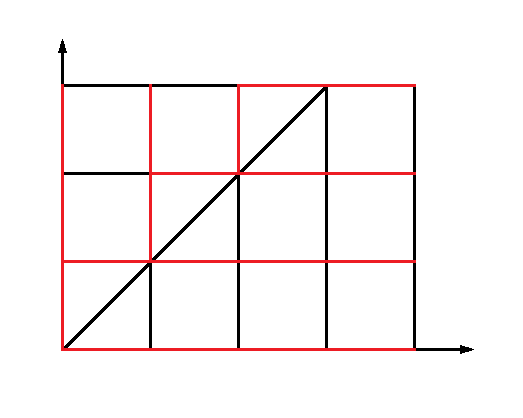
我们认为\((x,y)\)表示还剩\(x\)道答案为\(Yes\)的题,\(y\)同理.
认为向左走为回答\(Yes\),向下为\(No\).
然后你就会发现你啥也发现不了,
答题的过程就是从右上角\((n,m)\)走到\((0,0)\)的过程.
首选易知,我们应该尽可能的让我们的回答尽可能的向\(x=y\)这条直线靠拢.
这个是显然的,因为我们要尽可能的让"无论答案是什么,我们的回答都是正确的"这一事件发生.
我们画出的红线,就是我们的最优策略.
而答案是不确定的,所以其实是"随便走"的"答案"和我们的最优策略的交点,就是我们对的题的数目.
我们可以先随便画出一种答案.
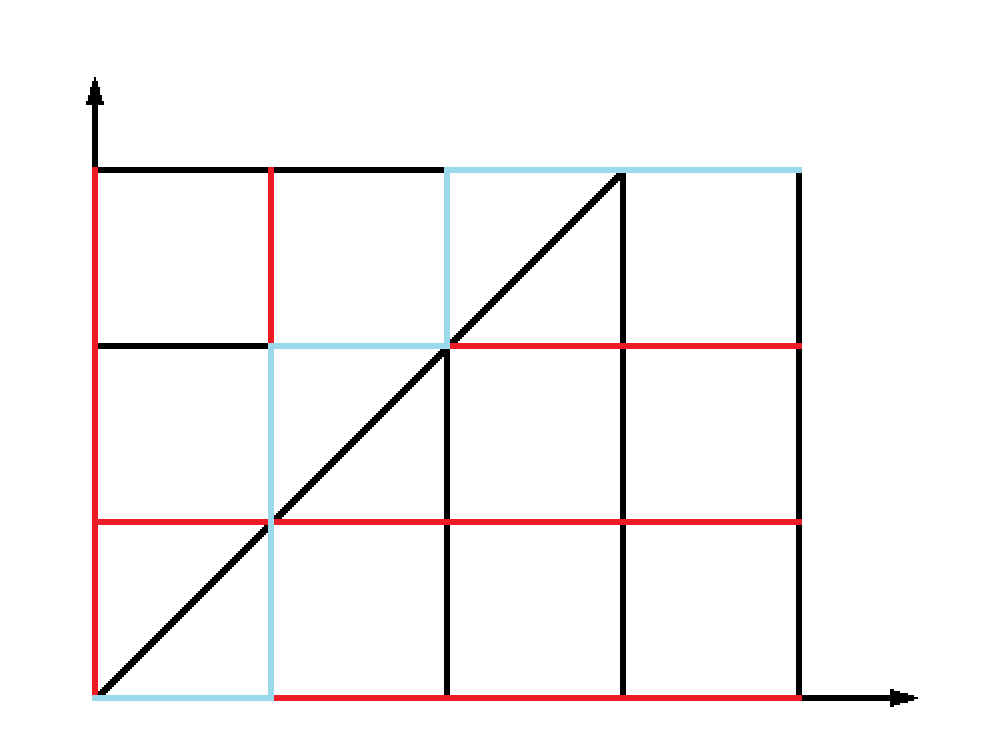
显然,我们可以把\(x=y\)这条直线以上的部分翻折下来——这对结果没有影响.
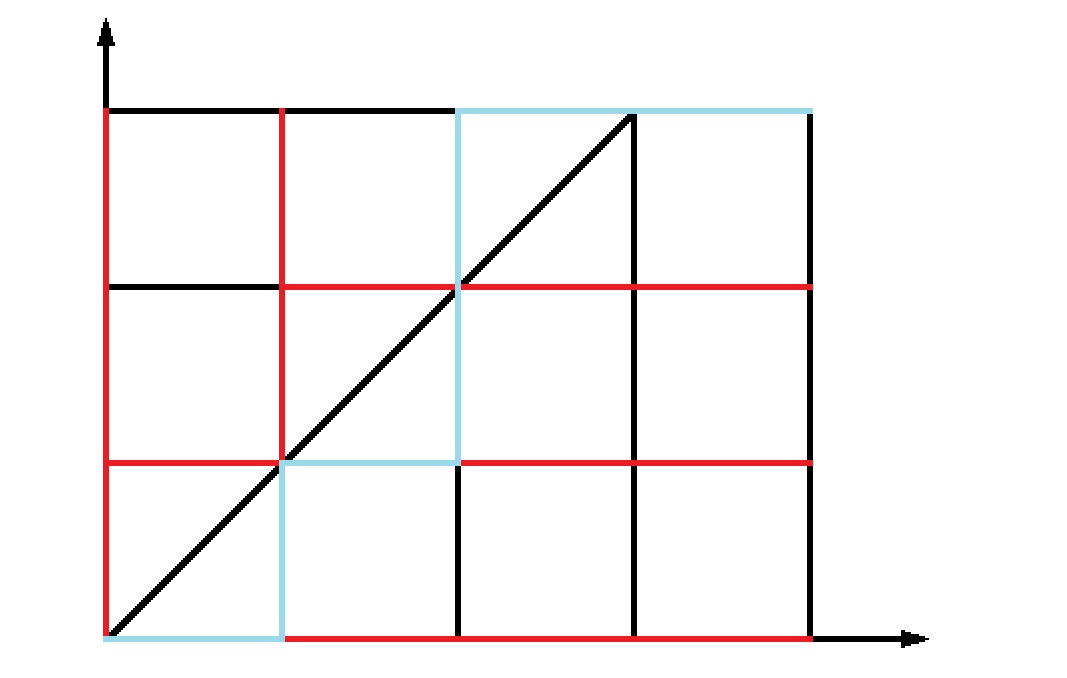
先抛开竖直的不看,
我们所有的横线都在最优策略所在的红线上,
所以这些横线的总贡献即为\(n\).
但这样只计算了\(x \neq y\)的情况.
再来计算\(x=y\)的情况.
显然我们需要求出经过\(x=y\)这条直线上某一点的概率.
先求出经过某一点的方案数:
\[\binom{n-i+m-i}{n-i} * \binom{i+i}{i}
\]
再除以$$\binom{n+m}{n}$$
因为此时向左走和向下走的概率是一样的,所以他们的贡献均为$ \frac{1}{2} $
总起来,可得
\[ans=
\sum_{i=1}^{min(n,m)}
\binom{n+m-2i}{n-i}
\binom{2i}{i} *
\frac{1}{2 \binom{n+m}{n} }*
max(n,m)
\]
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define endl '\n'
const int N=5e6;
const int mod=998244353;
#define int unsigned long long
#define Croll(i,l,r) for(int i=l;i<=r;++i)
#define Troll(i,l,r) for(int i=l;i>=r;--i)
//////////
namespace solve
{
int n,m,ans;
int f[N<<1],g[N<<1];
int C(int,int);
int qp(int,int);
void Wonder_of_U();
}using namespace solve;
//////////
namespace rw
{
il int read();
il void write(int);
il void Write(int);
}using namespace rw;
//////////
main()
{
n=read();m=read();
if(n<m)swap(n,m);
Wonder_of_U();
Croll(i,1,m)
ans=(ans+C(2*i,i)*C(n+m-2*i,n-i)%mod*g[2]%mod)%mod;
ans=(ans*qp(C(n+m,n),mod-2)%mod);
ans=(ans+n)%mod;
cout<<ans<<endl;
}
//////////
namespace solve
{
int C(int n,int m)
{
return f[n]*g[m]%mod*g[n-m]%mod;
}
int qp(int x,int k)
{
int ans=1;
while(k)
{
if(k & 1)ans=ans*x%mod;
x=x*x%mod;k>>=1;
}
return ans;
}
void Wonder_of_U()
{
f[0]=1;g[0]=1;
Croll(i,1,n<<1)
f[i]=f[i-1]*i%mod,
g[i]=g[i-1]*qp(i,mod-2)%mod;
}
}
//////////
namespace rw
{
il void write(int x)
{Write(x);cout<<endl;}
il int read()
{
int f=1,x=0;char w=getchar();
while(w<'0'||w>'9')
{if(w=='-')f=-1;w=getchar();}
while(w>='0'&&w<='9')
{x=(x<<3)+(x<<1)+(w^48);w=getchar();}
return f*x;
}
il void Write(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) Write(x/10);
putchar(x%10+'0');
}
}