拓扑排序学习笔记

ccr's notebook / 2023-08-25 / 原文

思想

拓扑，一看就是从图的开始开始开拓，并按被开拓到的顺序排序

拓扑排序的思想如下：

将入度为 \(0\) 的点删除，并记录它被删除的顺序，直到没有点则结束程序

图解

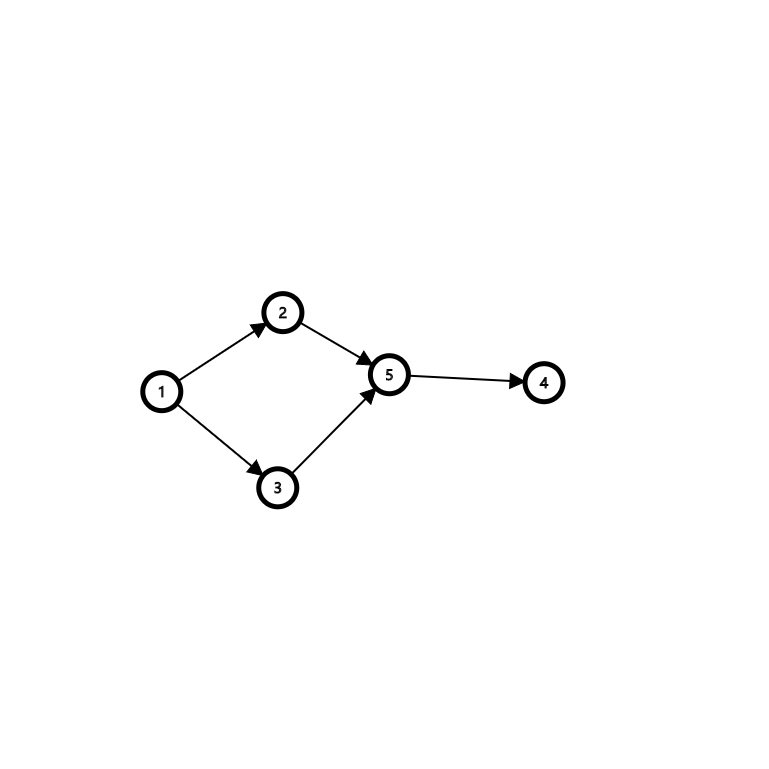
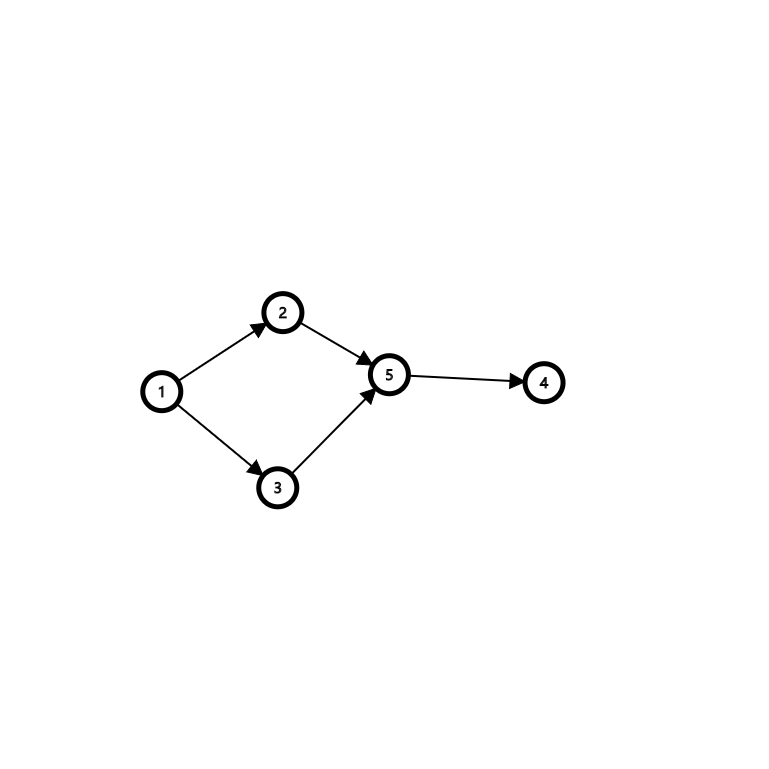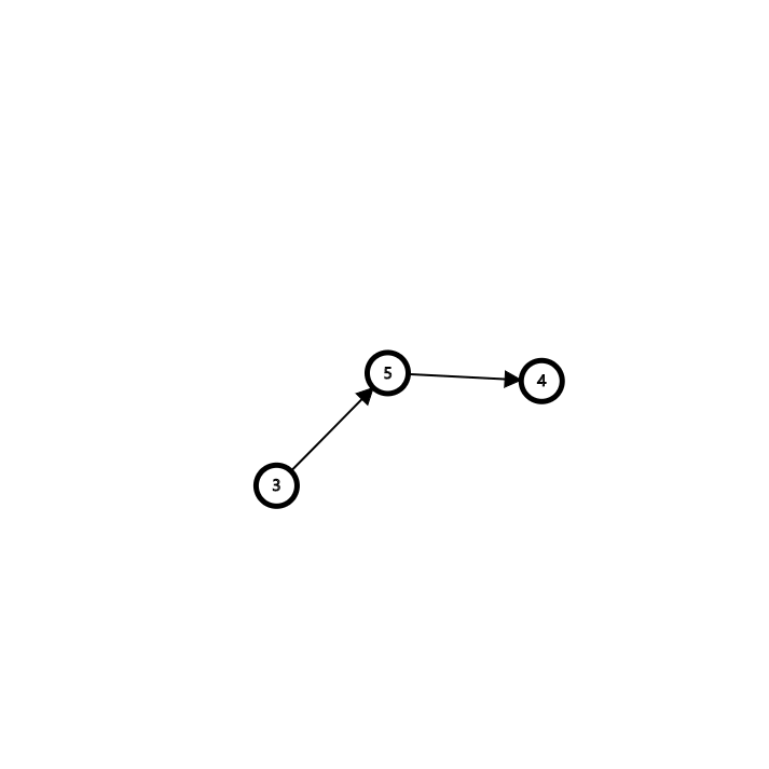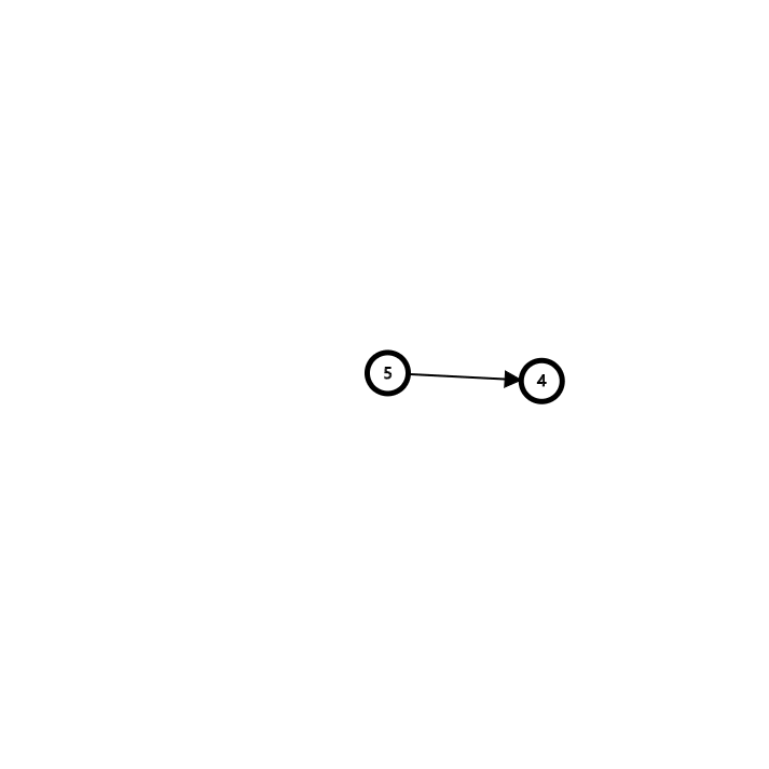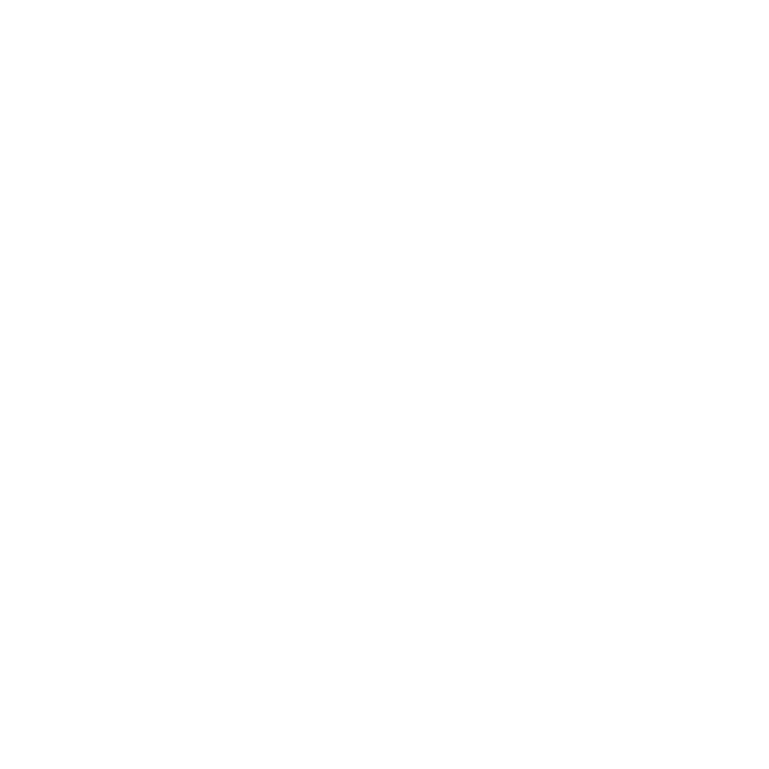
如本图的拓扑序就为 1 2 3 5 4

1.发现1入度为0

删除1，2/3的入度减\(1\)

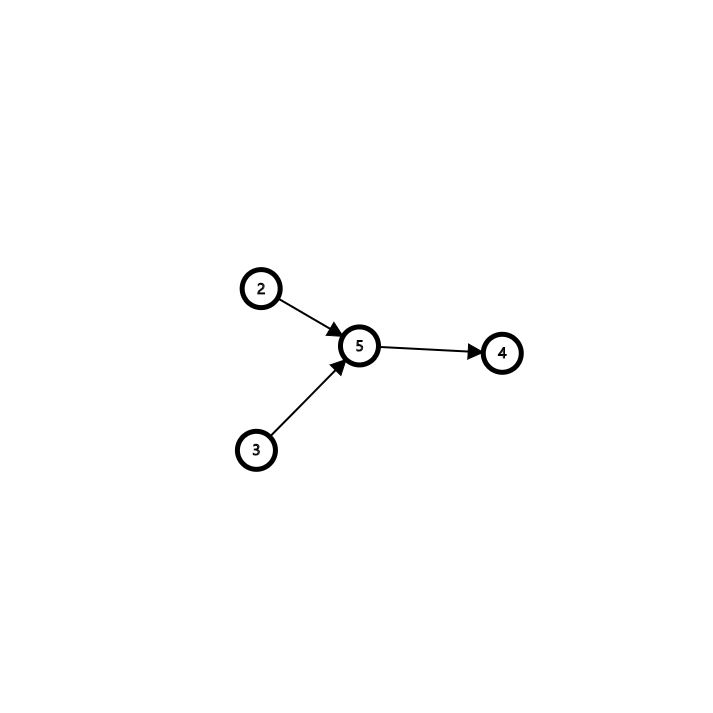
2.发现2入度为0

删除2，5的入度减\(1\)

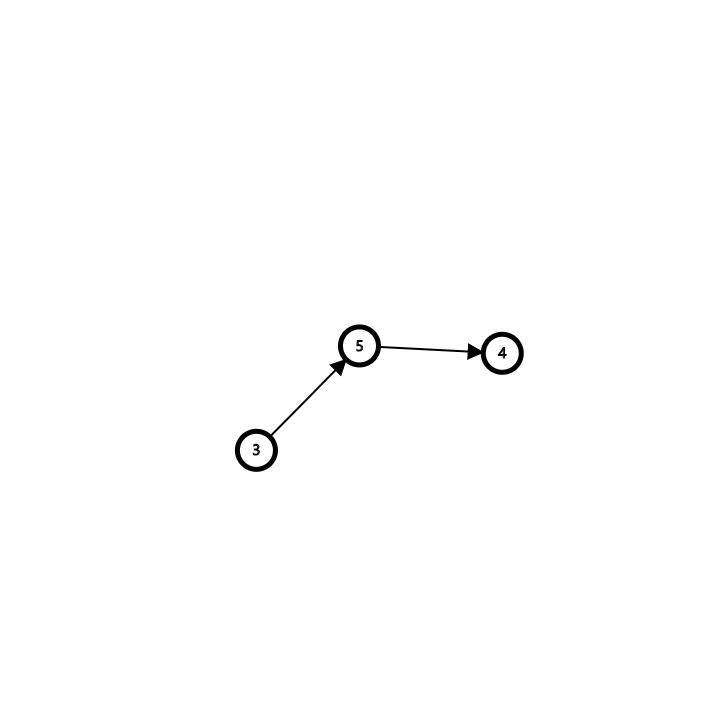
3.发现3入度为0

删除3，5的入度减\(1\)

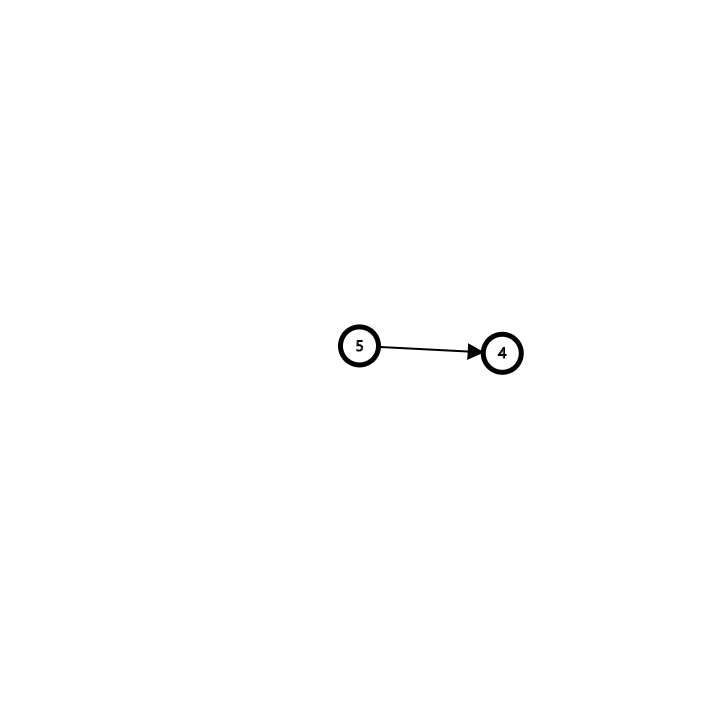
4.发现5入度为0

删除5，4的入度减\(1\)

5.发现4入度为0

删除4，发现没有点了，结束程序

全程

代码

代码也十分简单（甚至比思维还简单）：

#include<bits/stdc++.h>
using namespace std;
bool b[100001];
int fat[100001];
vector<int>v[100001];
int main(){
	int n,m=0;
	cin>>n;
	for(int i=1;i<=n;i++){
		int x,y;
		cin>>x>>y;
		v[x].push_back(y);
		fat[y]++;//记录入度
	}
	queue<int>q;
	for(int i=1;i<=n;i++){
		if(fat[i]==0){//将入度为0的点入队
			q.push(i);
			b[i]=1;
		}
	}
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<v[u].size();i++){
			int nn=v[u][i];
			fat[nn]--;//入度减少
			if(fat[nn]==0){
				q.push(nn);//将入度为0的点入队
				b[nn]=1;
			}
		}
	}
	for(int i=1;i<=n;i++){
		if(!b[i])cout<<i<<" ";	//也可以判断环上的点
	}
	return 0;
}

例题

P8655 [蓝桥杯 2017 国 B] 发现环

点击查看代码

#include<bits/stdc++.h>
using namespace std;
bool b[100001];
int fat[100001];
vector<int>v[100001];
int main(){
	int n,m=0;
	cin>>n;
	for(int i=1;i<=n;i++){
		int x,y;
		cin>>x>>y;
		v[x].push_back(y);
		v[y].push_back(x);
		fat[x]++;
		fat[y]++;
	}
	queue<int>q;
	for(int i=1;i<=n;i++){
		if(fat[i]==1){
			q.push(i);
			b[i]=1;
		}
	}
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<v[u].size();i++){
			int nn=v[u][i];
			fat[nn]--;
			if(fat[nn]==1){
				q.push(nn);
				b[nn]=1;
			}
		}
	}
	for(int i=1;i<=n;i++){
		if(!b[i])cout<<i<<" ";	
	}
	return 0;
}

B3644 【模板】拓扑排序 / 家谱树

字典序最小

有时会有要字典序最小的情况，这是开个大根堆即可

点击查看代码

#include<bits/stdc++.h>
using namespace std;
bool b[100001];
int fat[100001],ans[100001];
vector<int>v[100001];
int main(){
	int T=0;int n,m=0;
	cin>>T;
	while(T--){
		for(int i=1;i<=n;i++){
			fat[i]=0;
			v[i].clear();
			b[i]=0;
		}
		cin>>n>>m;
		for(int i=1;i<=m;i++){
			int x,y;
			cin>>x>>y;
			v[y].push_back(x);
			fat[x]++;
		}
		priority_queue<int>q;
		for(int i=1;i<=n;i++){
			if(fat[i]==0){
				q.push(i);
				b[i]=1;
			}
		}
		int tp=0;
		while(!q.empty()){
			int u=q.top();
			tp++;
			ans[tp]=u;
			q.pop();
			for(int i=0;i<v[u].size();i++){
				int nn=v[u][i];
				fat[nn]--;
				if(fat[nn]==0){
					q.push(nn);
					b[nn]=1;
				}
			}
		}
		if(tp<n){
			cout<<"Impossible!"<<endl;
			continue;
		}
		for(int i=n;i>=1;i--){
			cout<<ans[i]<<" ";
		}
		cout<<endl;
	}
	return 0;
}

唯一解问题

思路一：开三个不同记录方式的堆

bool check(int kk){
	queue<int>q;
	priority_queue<int>q1;
	priority_queue<int, vector<int>, greater<int> >q2;
	int op=0;
	for(int i=1;i<=n;i++){
		ru[i]=0;
	}
	for(int i=1;i<=n;i++){
		for(int j=0;j<v[i].size();j++){
			ru[v[i][j].to]++;
		}
	}
	for(int i=1;i<=n;i++){
		if(!ru[i]){
			q.push(i);
			q1.push(i);
			q2.push(i);
		}	
	}
	while(!q.empty()){
		int u=q.front(),u1=q1.top(),u2=q2.top();
		q.pop();q1.pop();q2.pop();
		if(u!=u1||u!=u2||u1!=u2)return 0;
		op++;
		for(int i=0;i<v[u].size();i++){
			int nn=v[u][i].to;
			ru[nn]--;
			if(!ru[nn]){
				q.push(nn);
				q1.push(nn);
				q2.push(nn);
			}
		}
	}
	//cout<<kk<<"/"<<op<<endl;
	if(op==n)return 1;
	else return 0;
}

思路二：队内判断

很容易证明只有队内只有一个数时才有唯一解，代码如下：

bool check(int kk){
	queue<int>q;
	int op=0;
	for(int i=1;i<=n;i++){
		ru[i]=0;
	}
	for(int i=1;i<=n;i++){
		for(int j=0;j<v[i].size();j++){
			ru[v[i][j].to]++;
		}
	}
	for(int i=1;i<=n;i++){
		if(!ru[i]){
			q.push(i);
		}	
	}
	while(!q.empty()){
		int u=q.front();
		q.pop();
		if(!q.empty())return 0;
		op++;
		for(int i=0;i<v[u].size();i++){
			int nn=v[u][i].to;
			ru[nn]--;
			if(!ru[nn]){
				q.push(nn);
			}
		}
	}
	if(op==n)return 1;
	else return 0;
}