KMP学习笔记
KMP
KMP是一种非常有用的算法,可以将字符串匹配的复杂度由 \(O(nm)\) 降到 \(O(n+m)\)
朴素算法
学过语言就会朴素算法,这里只给出伪代码:
for(i=0->n-1){
for(j=i>m-i){
if(s[i]!=s[j])goto fg;
}
cout<<i<<endl;
fg:;
}
时间复杂度 \(O(nm)\)。
KMP
KMP是基于DP的一种字符串匹配算法。
他先扫一遍模式串,建立 next 数组。
再通过 next 数组自动判断可以文本串当前位置能匹配到模式串第几个。
这听起来很神奇,但做起来更神奇。
图解
建立失配指针
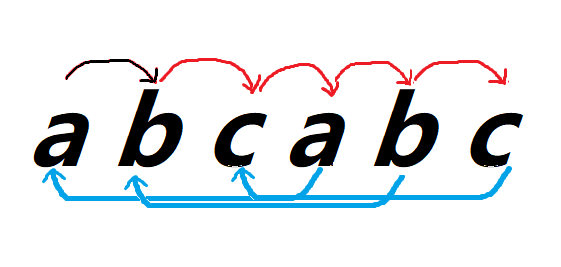
假设模式串为abcabc
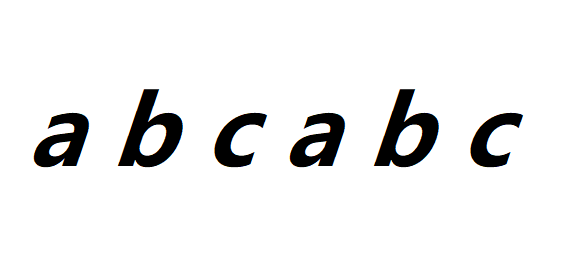
我们令红色箭头为匹配后的推进,蓝色箭头为失配后的推进。
next[0]
只有a才能推进,所以只有next[0]如果相同则推进至 1
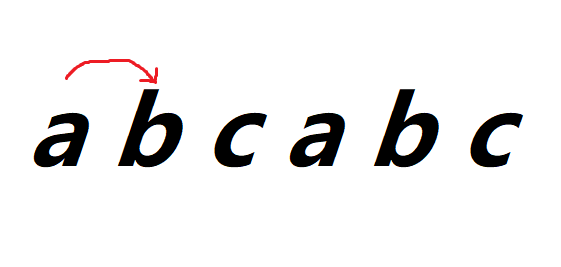
next[1]
只有b才能推进,所以只有next[1]如果相同则推进至 2
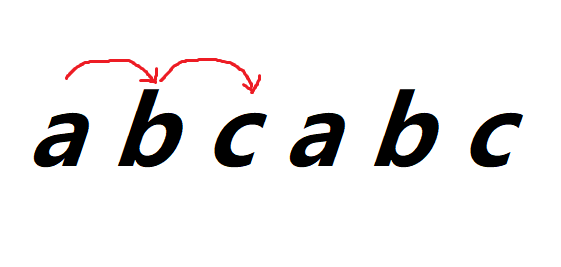
next[2]
同理,只有c才能推进,所以只有next[2]如果相同则推进至 3
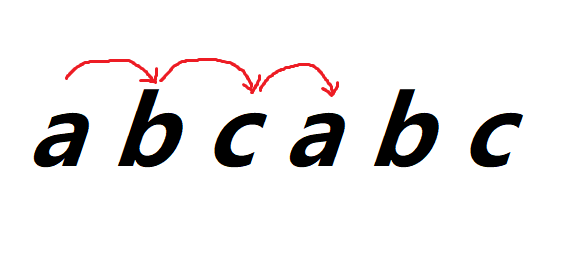
next[3]
从这里开始推进就不讲了。
当a失配时,我们看到它与前面的a有相同的前缀,所以a的失配指针为0
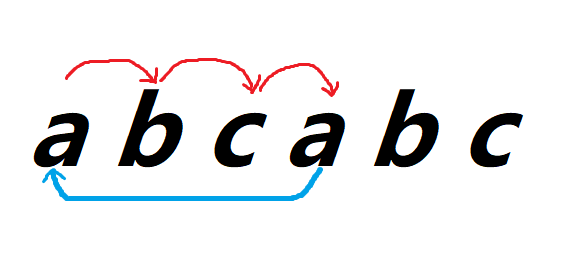
next[4]
当b失配时,我们看到它与前面的ab有相同的前缀,所以b的失配指针为1

next[5]
当c失配时,我们看到它与前面的abc有相同的前缀,所以c的失配指针为3
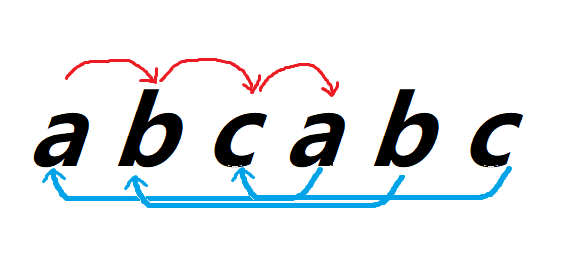
结果
结果如下图:
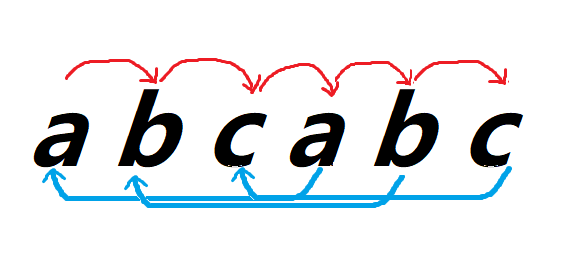
匹配
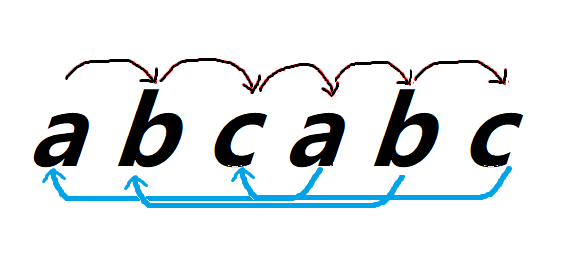
假设文本串为abcdababcabc。
黑色为当前走的箭头。
abc
直接跳到了3
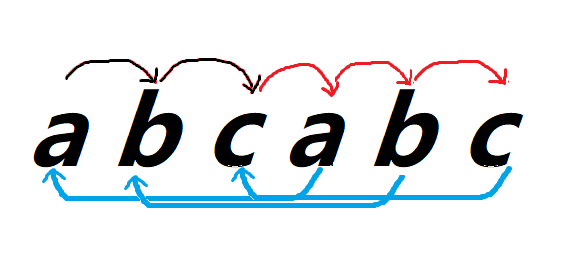
d
失配了,因为模式串中没有一个d,所以直接跳到了0

ab
直接跳到了2
a
失配了,因为模式串中上第一个a在1,所以直接跳到了1

bcabc
直接跳到了5,匹配成功!
代码
P3375 【模板】KMP 字符串匹配
#include<bits/stdc++.h>
using namespace std;
#define int long long
int nex[5000001]={0};
void KMP(string s){
int j=0;
nex[0]=1;
for(int i=2;i<s.size();i++){
while(j&&s[i]!=s[j+1])j=nex[j];//找上一个前缀相同的
if(s[j+1]==s[i])j++;
nex[i]=j;//建立匹配指针
}
}
void goo(string s,string s2,int a){
int j=0;
for(int i=1;i<s.size();i++){
while(j&&s[i]!=s2[j+1])j=nex[j];//运行失配指针
if(s[i]==s2[j+1])j++;
if(j==a){//匹配完成
cout<<i-a+1<<endl;//输出
j=nex[j];//下一个
}
}
}
signed main(){
string a1,a2;
cin>>a1>>a2;
a1=" "+a1;
a2=" "+a2;
KMP(a2);
goo(a1,a2,a2.size()-1);
for(int i=1;i<a2.size();i++)cout<<nex[i]<<" ";
return 0;
}