8.21 后记
关于时间复杂度
原来这么麻烦
有5种符号:
\(Θ:Θ(𝑔(𝑛))=\{𝑓(𝑛):∃𝑐_1,𝑐_2,𝑛_0:∀𝑛≥𝑛_0:0≤𝑐_1 𝑔(𝑛)≤𝑓(𝑛)≤𝑐_2 𝑔(𝑛)\}\)
\(O:O(𝑔(𝑛))=\{𝑓(𝑛):∃𝑐_1,𝑛_0:∀𝑛≥𝑛_0:0≤𝑓(𝑛)≤𝑐_1 𝑔(𝑛)\}\)
\(Ω:Ω(𝑔(𝑛))=\{𝑓(𝑛):∃𝑐_1, 𝑛_0:∀𝑛≥𝑛_0:0≤𝑐_1 𝑔(𝑛)≤𝑓(𝑛)\}\)
\(o:o(𝑔(𝑛))=\{𝑓(𝑛):∃𝑛_0:∀𝑐_1>0,𝑛≥𝑛_0:0≤𝑓(𝑛)≤𝑐_1 𝑔(𝑛)\}\)
\(\omega :\omega(𝑔(𝑛))=\{𝑓(𝑛):∃𝑛_0:∀𝑐_1>0,𝑛≥𝑛_0:0≤𝑐_1 𝑔(𝑛)≤𝑓(𝑛)\} \)
等号
\(𝑓(𝑛)=𝑂(𝑔(𝑛))\),表示能从 \(𝑂(𝑔(𝑛))\) 中可以选出一个函数 \(ℎ(𝑛)\) 使得等号成立
传递性
\(𝑓(𝑛)=Θ(𝑔(𝑛))∧𝑔(𝑛)=Θ(ℎ(𝑛))⇒𝑓(𝑛)=Θ(ℎ(𝑛))\)
\(𝑓(𝑛)=O(𝑔(𝑛))∧𝑔(𝑛)=O(ℎ(𝑛))⇒𝑓(𝑛)=O(ℎ(𝑛))\)
\(𝑓(𝑛)=Ω(𝑔(𝑛))∧𝑔(𝑛)=Ω(ℎ(𝑛))⇒𝑓(𝑛)=Ω(ℎ(𝑛))\)
\(𝑓(𝑛)=o(𝑔(𝑛))∧𝑔(𝑛)=o(ℎ(𝑛))⇒𝑓(𝑛)=o(ℎ(𝑛))\)
\(𝑓(𝑛)=\omega (𝑔(𝑛))∧𝑔(𝑛)=\omega (ℎ(𝑛))⇒𝑓(𝑛)=\omega (ℎ(𝑛))\)
自反性
\(𝑓(𝑛)=Θ(𝑓(𝑛))\)
\(𝑓(𝑛)=Ω(𝑓(𝑛))\)
\(𝑓(𝑛)=Ο(𝑓(𝑛))\)
对称性
\(𝑓(𝑛)=Θ(𝑔(𝑛))⇔ 𝑔(𝑛)=Θ(𝑓(𝑛))\)
\(𝑓(𝑛)=𝑂(𝑔(𝑛))⇔𝑔(𝑛)=Ω(𝑓(𝑛))\)
\(𝑓(𝑛)=𝑜(𝑔(𝑛))⇔𝑔(𝑛)=\omega (𝑓(𝑛))\)
类比
\(Θ\) 的性质与 \(=\) 相同
\(O\) 的性质与 \(≤\) 相同
\(Ω\) 的性质与 \(≥\) 相同
\(o\) 的性质与 \(<\) 相同
\(\omega\) 的性质与 \(>\) 相同
思考:\(n\) 与 \(n^{1+\sin n}\) 能够比较吗

分治
将大小为 \(n\) 的问题分为 \(a\) 个 大小为 \(\frac{n}{b}\) 的子问题,然后合并
归并排序 \(T(n)=2T(\frac{n}{2})+O(n)\)
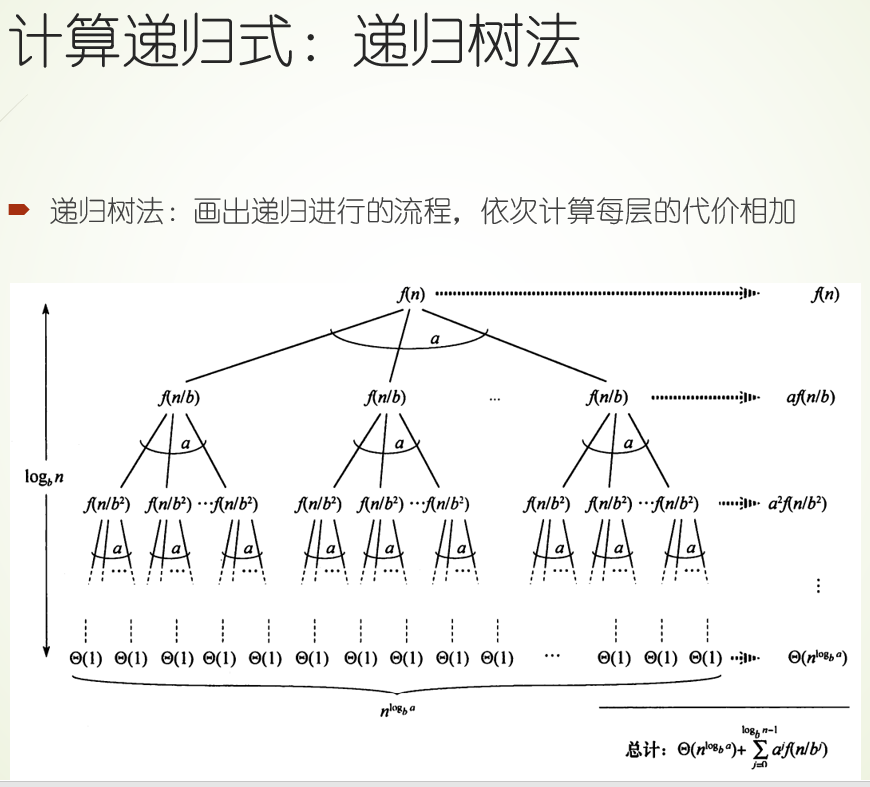
主定理

Top K
