CSP-J 模拟赛 C 题讲解
前言
鸣谢:感谢 LHT 大佬的推荐、GCK 大佬的提醒以及 LBJ 大佬帮我接龙。
原题链接
随手给大家扔一份吧。
题目大意
给你一个 \(1\) 到 \(n\) 的数列,当 \(a_i < a_{i-1}\) 的时候(大于号和小于号其实不用管,因为最后所有方案都会遍历到,对答案没有影响)放置一个红色灯笼,否则放置一个绿色灯笼。问正好放置 \(k\) 个红灯笼的排列方式有几种。由于答案很大,所以将答案对 \(2012\) 取模。
简化题意:
对于 \(1\) 到 \(n\) 的所有排列,在其中插入不等号,其中恰好有 \(k\) 个小于号的方案数。
No.1 30pts 暴力
思路
既然是询问有几个满足要求的排列,我们就可以用 next_permutation 枚举全排列,记录下答案数。
代码
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
int n,k,ans;
int a[1000006];
signed main(){
cin>>n>>k;
for(int i=1;i<=n;i++)a[i]=i;
do{
int cnt=0;
for(int i=2;i<=n;i++)
if(a[i-1]<a[i])cnt++;//注意是插入小于号的方案数(其实改成大于号也不会有影响
if(cnt==k)ans++;//k 个红灯笼
ans%=2012;//取模
}while(next_permutation(a+1,a+n+1));//枚举全排列
cout<<ans<<endl;
return 0;
}
No.2 100pts 正解
思路
动态规划 DP。
维护一个数组 \(dp\),\(dp_{i,j}\) 代表前 \(i\) 个数字构成的数列中 \(<\) 有 \(j\) 个的方案数。那么 \(>\) 就有 \(i-j-1\) 个,为什么要 \(-1\) 呢?因为 \(i\) 个数的数列中一共只有 \(i-1\) 个间隔,也就是有 \(i-1\) 个不等号(这类似于小学的种树问题,想必大家是可以理解的),那么 \(i-1\) 个不等号中有 \(j\) 个 \(<\),自然 \(>\) 的数量就是剩下的 \(i-1-j\) 个了。
既然是用到 DP 了,那么我们换一种方法来理解此题:“把数字从小到大插入到数列中”。
按照上述的理解,我们接下来再来考虑一下转移的方程式:
我们可以发现,数 \(i\) 插入的位置无非有两种情况:插在原来是 \(<\) 的位置或插在原来是 \(>\) 的位置。
举个栗子:
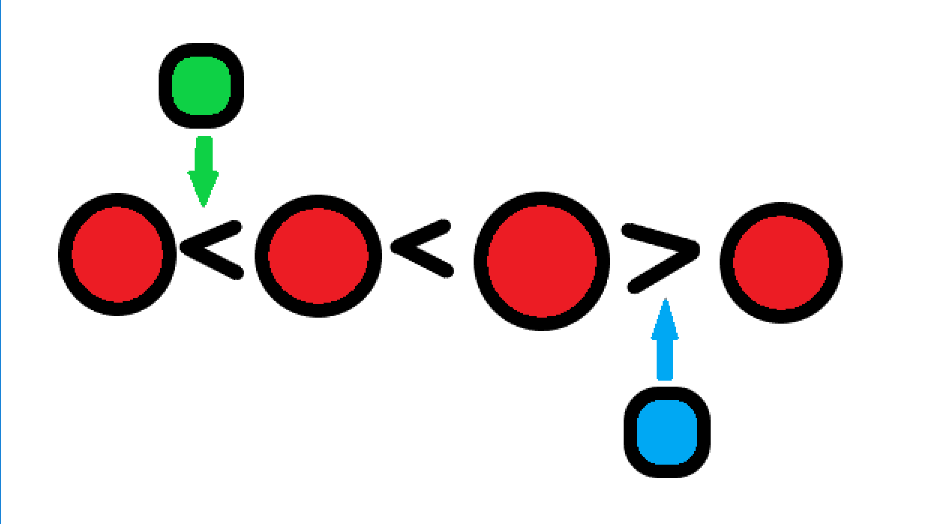
在这幅图中,绿色的属于第一种情况:插在原来是 \(<\) 的位置上,而蓝色就对应的属于第二种情况:插在原来是 \(>\) 的位置上。
接下来我们来分情况讨论:
- 插在 \(<\) 的位置上:

如图所示,我们对比原先的数列可以发现,该种放置方式会使 \(<\) 的数量不变,\(>\) 的数量增加一。(这里注意,插入的数一定是当前数列中最大的,因为我们是按照从小到大的顺序插入数字的)。
- 插在 \(>\) 的位置上:

同样如图所示,对比原先数列发现,此种放置方式会使 \(>\) 的数量不变,\(<\) 的数量加一。
分类讨论之后,综上所述,我们就可以得到了转移方程式:
\(dp_{i,j} = dp_{i-1,j-1} \times (i-j-1) + dp_{i-1,j} \times (j)\)
But......
这个转移方程真的正确吗?
乍一看确实没毛病对吧,每次的方案数都等于 放在大于号位置的方案数 + 放在小于号位置的方案数。但是我们考虑,难道插入的这个数字只能放在两个数之间吗?
答案是 false 的,插入的数还可以放到整个数列的最左端或最右端,like:

所以说,可以插入的位置不仅仅是这个数列中的一个位置,也可以放在这个数列的边缘,所以最终的转移方程式其实是:
\(dp_{i,j} = dp_{i-1,j-1} \times (i-j) + dp_{i-1,j} \times (j+1)\)(即将 \(>\) 和 \(<\) 的可以插入的位置分别 \(+1\))。
代码
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int mod=2012;
int n,k,dp[1005][1005];
signed main(){
cin>>n>>k;
for(int i=1;i<=n;i++)dp[i][0]=1;//注意要赋初值
for(int i=2;i<=n;i++)
for(int j=1;j<=n;j++)
dp[i][j]=(dp[i-1][j-1]*(i-j)+dp[i-1][j]*(j+1))%mod;//转移方程式
cout<<dp[n][k]<<endl;//n 个数 k 个小于号
return 0;
}