\(SG\)函数

首先定义就不用我讲了吧，还不会的自己查下看看 。

我们主要想把 \(SG\) 函数这个玄妙的东西的运用搞清楚。

再进一步理解一下吧：

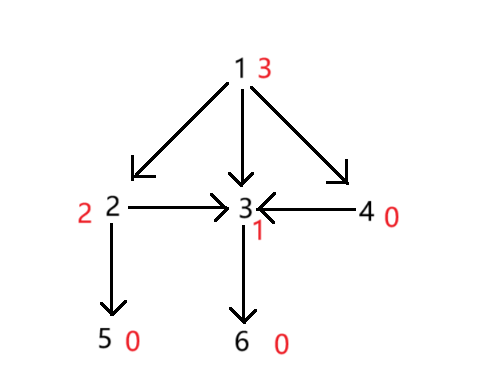
黑色数字是节点编号，红色是 SG 函数值

看下它的过程：

1. 首先 \(5\) 和 \(6\) 没有后继节点，为必败态，先赋值为 \(0\)
2. \(3\) 只有 \(6\) 一个后继节点，计算得 \(1\)
3. 现在我们已经得出了 \(2\) 和 \(4\) 的所有后继节点的值，进而给它赋值
4. 最后统计 \(1\) 的子节点中含有的值有\(0，1，2\) 取值 \(3\)

最关键是定义知道了这个东西怎么用呢？首先我们需要明白两点：

1. \(SG\) 函数是 \(xor\) 起来用的，故而可能存在两种状态 \(xor\) 起来并不能达到必胜/必败态，故而不能仅仅只赋值为 \(0\) 和 \(1\) 。
2. \(SG\) 函数的值是可以由我们任意决定的，我们主要通过搜索的方式进行赋值。

那么我们来抓个典型

【SSLOJ 1633】B君的游戏

\(B\)君和\(L\)君要玩一个游戏。刚开始有 \(n\) 个正整数 \(a_i\) 。

双方轮流操作。每次操作，选一个正整数 \(x\)，将其移除，再添加 \(7\) 个数字 \(x_1,x_2...x_7\) 。要求对于 \(x_i\) ，满足 \(0\le x_i<x\) 且 \(x\ \&\ x_i = x_i\)

注意\(0\)不能被选取，所以这个游戏一定会结束，而谁无法操作谁就失败。

\(B\)君根据自己的经验，认为先手胜率高一点，所以\(B\)君是先手。

B君想知道自己是否必胜。

第一行一个整数\(n (1 \le n \le 100000)\)

以下 \(n\) 行 \(n\) 个数 \(a_i (0 \le a_i < 2^64)\)

输入样例

4
1
2
3
4

输出样例

B

基本思路

很显然，后继状态及结果至于 \(x\) 中 \(1\) 的个数有关，因为本质就是从 \(x\) 中选几个 \(1\) 出来嘛。这题我们暴力打出每种 \(1\) 的个数下的 \(SG\) 函数就可以了。

上代码，我们也借此了解一下 \(SG\) 函数是如何被计算的。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
const int M=7e7+10;
int sg[70];
bool vis[M]; 
inline void dfs(int num,int p,int ans,int cur){
//	搜索求解sg函数值 
//	num限制最大值,cur限制最小值,p控制递归层数
	if(p==0){
		vis[ans]=true;
		return;
	}
	for(int i=cur;i<num;i++){
		dfs(num,p-1,ans^sg[i],i);
	}
}
inline void init(){
	printf("{");
	sg[0]=0;
	for(int i=1;i<=64;i++){
		memset(vis,0,sizeof(vis));
		dfs(i,7,0,0);
		for(int j=0;j<M;j++){
			if(vis[j]==false){
				sg[i]=j;
				break;
			}
		}
		cout<<i<<":";
		printf("%d",(sg[i]));
		if(i<64) printf(",");
	}
	cout<<"}";
}
int main(){
//	ios::sync_with_stdio(false);
	init();
	return 0;
}

我们先仔细看看搜索部分

inline void dfs(int num,int p,int ans,int cur){
//	搜索求解sg函数值 
//	num限制最大值,cur限制最小值,p控制递归层数
	if(p==0){
		vis[ans]=true;
		return;
	}
	for(int i=cur;i<num;i++){
		dfs(num,p-1,ans^sg[i],i);
	}
}

Q1:为什么要用 \(p\) 来限制递归层数，而且可以在 \(init\) 中看到限制了 \(7\) 层？

这个 \(7\) 就是题目中说的选出 \(7\) 个数，因为选出来的数 \(1\) 的个数都比 \(x\) 要少，故而他们的 \(SG\) 值都算好了，将他们 \(xor\) 起来就可以得到当前答案了。

Q2：为什么要将他们的后继节点的 SG 值都异或起来呢？

因为我们可以发现实际上 \(SG\) 函数的用法就是异或起来，据此判断先后手必胜，详细证明会很麻烦。

O3为什么还要限制最小值呢？

因为仔细观察你就会发现这实际上是将全排列转换成了组合计数，减少了时间复杂度，删去了重复的递归，因为后面选择的数是严格大于等于前面选择的数的。

Q4： \(vis\) 数组是干什么用的？

这个显然就是进行 \(mex\) 运算的，记录后继状态中有那些值，然后向 \(init\) 中求解。

最后输出就像这样：

{1:1,2:2,3:4,4:8,5:16,6:32,7:64,8:128,9:255,10:256,11:512,12:1024,13:2048,14:3855,15:4096,16:8192,17:13107,18:16384,19:21845,20:27306,21:32768,22:38506,23:65536,24:71576,25:92115,26:101470,27:131072,28:138406,29:172589,30:240014,31:262144,32:272069,33:380556,34:524288,35:536169,36:679601,37:847140,38:1048576,39:1072054,40:1258879,41:1397519,42:2005450,43:2097152,44:2121415,45:2496892,46:2738813,47:3993667,48:4194304,49:4241896,50:4617503,51:5821704,52:7559873,53:8388608,54:8439273,55:8861366,56:11119275,57:11973252,58:13280789,59:16777216,60:16844349,61:17102035,62:19984054,63:21979742,64:23734709}
--------------------------------
Process exited after 104 seconds with return value 0
请按任意键继续. . .

我这里还加了编号，用的时候自然得去掉。

核心代码

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
ull sg[70]={0,1,2,4,8,16,32,64,128,255,256,512,
			1024,2048,3855,4096,8192,13107,16384,
			21845,27306,32768,38506,65536,71576,
			92115,101470,131072,138406,172589,240014,
			262144,272069,380556,524288,536169,679601,
			847140,1048576,1072054,1258879,1397519,
			2005450,2097152,2121415,2496892,2738813,
			3993667,4194304,4241896,4617503,5821704,
			7559873,8388608,8439273,8861366,11119275,
			11973252,13280789,16777216,16844349,
			17102035,19984054,21979742,23734709};
ull n,a,ans,sum;
int main() {
	ios::sync_with_stdio(false);
	cin>>n;
	while(n--){
		cin>>a;
		sum=0;
		while(a){
			a^=(a&(-a));
			sum++;
		}
		ans^=sg[sum];
	}
	if(ans) cout<<"B";
	else cout<<"L";
	return 0;
}

再抓个典型巩固一下

【luogu P10501】 Cutting Game

P.S.进一步可点击链接前往往洛谷参考题解。

题面翻译

【题目描述】

Urej 喜欢玩各种类型的沉闷游戏。他通常会邀请其他人和他一起玩。他说，玩这些游戏可以展现他的非凡智慧。最近，Urej 对一个新游戏产生了极大兴趣，而 Erif Nezorf 成为了牺牲品。为了摆脱玩这样一个沉闷游戏的痛苦，Erif Nezorf 请求你的帮助。这个游戏使用一个由 \(W * H\) 格网组成的矩形纸张。两名玩家轮流将纸张切割成两个矩形部分。在每个回合中，玩家可以横向或纵向切割，保持每个格网完整。经过 \(N\) 轮后，纸张将被切割成 \(N+1\) 片，然后在后续的回合中，玩家可以选择任意一片进行切割。如果一名玩家切割出一个只有一个格网的纸片，他就赢得了游戏。如果这两个人都非常清楚，你应该写一个问题来告诉是否先手的玩家能赢得游戏。

【输入格式】

输入包含多个测试用例。每个测试用例在一行中只包含两个整数 \(W\) 和 \(H (2 \le W , H \le 200)\)，分别表示原始纸张的宽度和高度。

【输出格式】

对于每个测试用例，应该只输出一行。如果先手的玩家能赢得游戏，则输出 "WIN"，否则输出 "LOSE"。

样例 #1

样例输入 #1

2 2
3 2
4 2

样例输出 #1

LOSE
LOSE
WIN

基本思路

这个也很显然，状态是什么？就是一张纸的长和宽嘛，长和宽就对应了它的 \(SG\) 值。可能有同学会疑问，可是我们裁出的是两张纸啊，不一定非要再这张上进行操作，在另一张纸上裁一刀周旋一下嘛。问题是我们最后要把各个状态的 \(SG\) 值异或起来啊，一定是会把两个状态（两张纸）异或起来才是答案嘛。

好了，就像上面说的，这次还是搜索求 \(SG\) 值吗？显然不会是，我们会用递归（这两个思想还是有点区别的）。上一道题的搜索是在搜什么？就是排列组合它的状态啊，我们这道题还要用上面这种方式找出它的所有后继状态吗？我们裁出的是两张，那直接 \(for\) 循环枚举裁出的长度就可以了。但这道题一定要注意，不能裁出含有一边长度为 \(1\) 的，那就是必败了（显然不符合博弈论双方都采用最优措施的设定了）

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=210;
const int S=7e4+10;
int sg[N][N],w,h;
inline int SG(int x,int y){
	if(sg[x][y]!=-1) return sg[x][y];
	bool vis[S];
	memset(vis,0,sizeof(vis));
	for(int i=2;i<x-1;i++) vis[SG(i,y)^SG(x-i,y)]=true;
	for(int i=2;i<y-1;i++) vis[SG(x,i)^SG(x,y-i)]=true;
	//计算
	for(int i=0;i<S;i++)if(vis[i]==false)
		return sg[x][y]=i;
}
int main(){
	ios::sync_with_stdio(false);
	memset(sg,-1,sizeof(sg));
	while(cin>>w>>h){
		if(SG(w,h)==0) cout<<"LOSE\n";
		if(SG(w,h)) cout<<"WIN\n";
	}
    return 0;
}

大家也可以看到这次不是预处理 \(SG\) 值了，而是在线算法求解，如果碰到哪个 \(SG\) 值还不知道的就直接递归求解就可以啦。

也可能有同学会疑惑对于必败点的问题，\(1*1\) 是必胜点，那么我们可以发现 \(2*2 , 2*3 ,3*2\) 就是必败点了，因为怎么裁都会裁出\(1*X\) 的纸。这里就不用考虑这个问题，因为到上述状态是因为会裁处一边为 \(1\) ，就无法计算，会自动赋值为 \(0\) 。

如果还想再被 SG 函数恶心一下由此进入

（于此更新：2024.10.22 ）

允许我再唠叨一道题！

【luogu P2953】 Cow Digit Game S

题目描述

贝茜和约翰在玩一个数字游戏．贝茜需要你帮助她．

游戏一共进行了\(G(1≤G≤100)\)场．第i场游戏开始于一个正整数\(Ni(l≤Ni≤1,000,000)\)．游

戏规则是这样的：双方轮流操作，将当前的数字减去一个数，这个数可以是当前数字的最大数码，也可以是最小的非0数码．比如当前的数是3014，操作者可以减去1变成3013，也可以减去4变成3010．若干次操作之后，这个数字会变成0．这时候不能再操作的一方为输家． 贝茜总是先开始操作．如果贝茜和约翰都足够聪明，执行最好的策略．请你计算最后的赢家．

比如，一场游戏开始于13.贝茜将13减去3变成10．约翰只能将10减去1变成9．贝茜再将9减去9变成0．最后贝茜赢．

输入格式

* Line 1: A single integer: G

* Lines 2..G+1: Line i+1 contains the single integer: N_i

输出格式

* Lines 1..G: Line i contains 'YES' if Bessie can win game i, and 'NO' otherwise.

样例 #1

样例输入 #1

2 
9 
10

样例输出 #1

YES 
NO

提示

For the first game, Bessie simply takes the number 9 and wins. For the second game, Bessie must take 1 (since she cannot take 0), and then FJ can win by taking 9.

基本思路

一定要审清楚题！只有两个转移方向，一个是减去最大数字，一个是减去最小非零数字。

我也不清楚这是不是 \(SG\) 函数，但直觉告诉我这应该是一个 \(SG\) 函数的变式。

首先我们申明一下博弈论的基本思想：

• 如果一个状态的后继状态存在必败状态，则该状态为必胜态。能使对手必败那不抓紧往那个方向转移？
• 如果一个状态的后继状态全部为必胜状态，则该状态为必败状态。因为没法使对手必败。

\(SG\) 函数为什么不设成 \(true\) 和 \(false\) 直接表示必胜或必败呢？像上一题，有多堆石子， \(1\) 和 \(1\) 异或起来就会变成 \(0\) ，这显然不合理嘛，因为这是个联合多点的局面，会存在两堆必胜态异或起来达不到必败状态的情况。

但是这题不一样。

我们要操作的是单点而非一个局面，意思就是说我们现在只有 \(mex\) 运算而没有 \(xor\) 运算。这么说就可以用 \(true\) 和 \(false\)表示了，而计算也依据上面的基本思想可以轻易地得出。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
int n,g;
bool f[N];
inline void getnum(int x,int &maxn,int &minn){
	maxn=1;minn=10;
	while(x){
		maxn=max(maxn,x%10);
		if(x%10>0&&x%10<minn) minn=x%10;//特别注意
		x/=10;
	}
}
int main(){
	ios::sync_with_stdio(false);
	//f中初始就全是false
	for(int i=1;i<10;i++)
		f[i]=true;//一步到位，必胜
	for(int i=10;i<N;i++){
		int p,q;
		getnum(i,q,p);
		if(f[i-p]==false&&p>0||f[i-q]==false&&q>0)//存在必败状态
			f[i]=true;
	} 
	cin>>g;
	while(g--){
		cin>>n;
		if(f[n]) puts("YES");
		else puts("NO");
	}
	return 0;
}

再送一道题做做，如果做出来了说明你已经上道了P4018 Roy&October之取石子