A 小 h 的几何

简单证一下圆心，九点圆就不写了。首先画出单位圆，圆形为 \(\text{O}\)，随便找到一个内接三角形 \(\triangle_{\text{ABC}}\)，然后找到中点连接出四个三角形，分成的四个三角形全等，且 \(\triangle_{\text{AEF}}\) 与 \(\triangle_{\text{EFG}}\) 关于 \(\text{EF}\) 的中点 \(\text{S}\) 对称。\(\triangle_{\text{ABC}}\) 与 \(\triangle_{\text{AEF}}\) 有 \(\frac{1}{2}\) 的位似关系，所以找到了 \(\triangle_{\text{AEF}}\) 的外心 \(O'\)，他在 \(\text{AO}\) 的中点处，然后根据点对称找到 \(\triangle_{\text{EFG}}\) 的外心 \(O''\)，因为 \(O'O''\) 与 \(OG\) 平行且相等，所以中间的四边形 \(O'O''GO\) 为平行四边形，然后 \(O''\) 就是点 \(G\) 向 \(\overrightarrow{OA}\) 平移 \(\frac{1}{2}\) 得到，得出结论 \(O''=\frac{A+B+C}{2}\)。

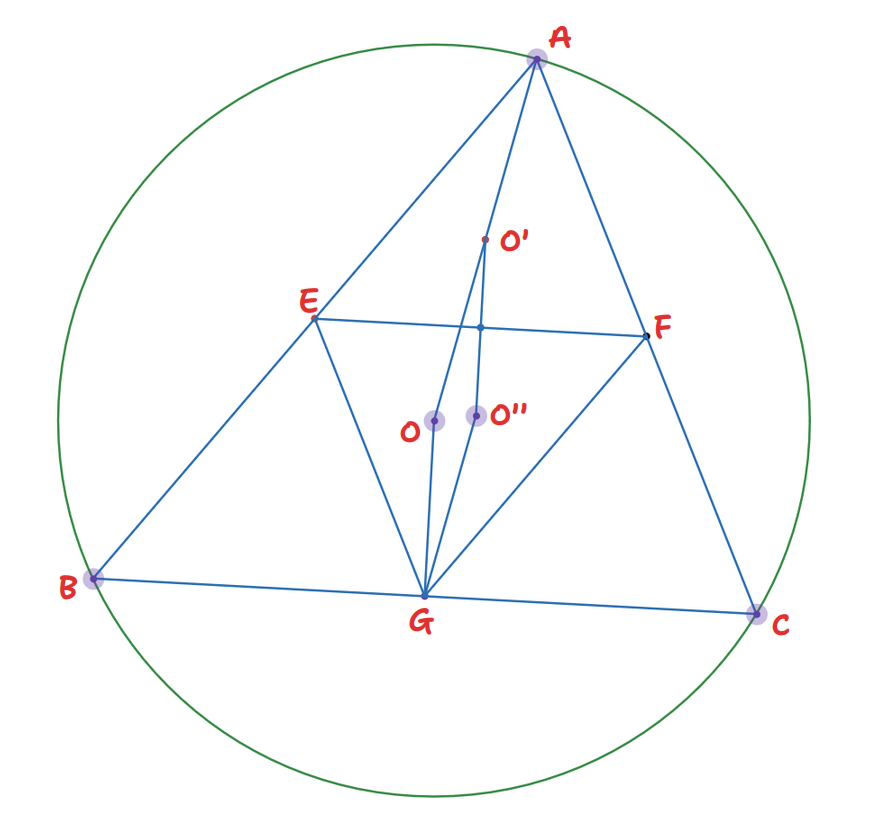
B 小 w 的代数

先考虑树咋做，枚举起点终点，以每个点为根搜一遍，维护一个栈，每次去栈里暴力找，时间复杂度 \(\mathcal{O}(n^3)\)。
看到仙人掌，考虑建圆方树，设 \(f_{i,j}\) 表示到了 \(i\) 点，以 \(j\) 点结尾的方案数，之前的栈本质上就是这个数组。仍然延续树的思路，在圆点直接算答案，在方点考虑环上的转移，找到环上的断点（进入点），发现对于一个环只有两种走法，所以都转移一下，环内的转移是无交的，但是进入节点都转移了两次，所以转移完后再减去就行了。

#include<bits/stdc++.h>
#define fi first
#define se second
#define pii std::pair<int,int>
#define eb emplace_back
typedef long long ll;
typedef unsigned long long ull;
std::mt19937 myrand(std::chrono::high_resolution_clock::now().time_since_epoch().count());
inline int R(int n){return myrand()%n+1;}
inline int read(){char ch=getchar();int x=0,f=1;for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);return x*f;}
const int N=1001,mod=998244353,inf=1e9;
inline void Min(int &x,int y){if(x>y)x=y;}
inline void Max(int &x,int y){if(x<y)x=y;}
inline void W(int &x,int y){x=(x+y)%mod;}
int n,m,low[N],dfn[N],dn,sta[N],top,cnt,f[N][N],tmp[N],ans,rt;
std::vector<int> e[N],g[N],node;
inline void tarjan(int x){
    sta[++top]=x;low[x]=dfn[x]=++dn;
    for(int v:e[x]){
        if(!dfn[v]){
            tarjan(v);low[x]=std::min(low[x],low[v]);
            if(low[v]==dfn[x]){
                ++cnt;
                while(sta[top+1]!=v){int x=sta[top--];g[cnt].eb(x);g[x].eb(cnt);}
                g[x].eb(cnt);g[cnt].eb(x);
            }
        }else low[x]=std::min(low[x],dfn[v]);
    }
}
inline void dfs(int x,int fa){
    if(x<=n){
        for(int i=rt;i<=x;++i)W(ans,f[x][i]);
        for(int i=rt;i<x;++i)W(f[x][x],f[x][i]);
    }else{
        int cut,s=g[x].size();
        for(int i=0;i<s;++i)if(g[x][i]==fa){cut=i;break;}
        node.clear();
        for(int i=(cut+1)%s;i!=cut;i=(i+1)%s)node.eb(g[x][i]);
        for(int i=rt;i<=n;++i)tmp[i]=f[fa][i];
        for(int v:node){
            for(int i=rt;i<=n;++i)W(f[v][i],tmp[i]);
            for(int i=rt;i<v;++i)W(tmp[v],tmp[i]);
        }
        for(int i=rt;i<=n;++i)tmp[i]=f[fa][i];
        std::reverse(node.begin(),node.end());
        for(int v:node){
            for(int i=rt;i<=n;++i)W(f[v][i],tmp[i]);
            for(int i=rt;i<v;++i)W(tmp[v],tmp[i]);
        }
        for(int v:node)for(int i=rt;i<=n;++i)W(f[v][i],-f[fa][i]);
    }
    for(int v:g[x])if(v!=fa)dfs(v,x);
}
signed main(){
    freopen("algebra.in","r",stdin);freopen("algebra.out","w",stdout);
    std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
    cnt=n=read();m=read();for(int i=1;i<=m;++i){int u=read(),v=read();e[u].eb(v);e[v].eb(u);}
    tarjan(1);
    for(int i=1;i<=n;++i){for(int j=1;j<=n;++j)for(int k=1;k<=n;++k)f[k][j]=0;f[i][i]=1;dfs(rt=i,i);}
    std::cout<<(ans)%mod<<'\n';
}

C 小 y 的数论

没看懂题

D 小 j 的组合

换下题目顺序和描述，这题就成签到了。
找哈密顿是 NPC 问题，所以这题做不了，你说的对，但是这是一棵树，起点和终点之间的路径是唯一的，所以只要从起点到终点搜子树即可。
首先考虑一棵树在不是链的情况下一定没有哈密顿通路，因为要进子树，所以加点就相当于让一个点可以多走一次，考虑路径的起点和终点构成的一条链，长度为 \(len\)，\(g=n-len\)，证明的话，手玩一下发现，对于一个节点需要复制的次数等于不在路径上的儿子数，所以复制的总次数就是链外节点数。
让 \(g\) 最小就是让链最长，找直径即可。时间复杂度线性，为啥这题不开到 \(10^6\)。

#include<bits/stdc++.h>
#define fi first
#define se second
#define pii std::pair<int,int>
#define eb emplace_back
typedef long long ll;
typedef unsigned long long ull;
std::mt19937 myrand(std::chrono::high_resolution_clock::now().time_since_epoch().count());
inline int R(int n){return myrand()%n+1;}
inline int read(){char ch=getchar();int x=0,f=1;for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);return x*f;}
const int N=100+10,mod=998244353,inf=1e9;
inline void Min(int &x,int y){if(x>y)x=y;}
inline void Max(int &x,int y){if(x<y)x=y;}
inline void W(int &x,int y){x=(x+y)%mod;}
int n,st,en,f[N],dis[N],vis[N];
std::vector<int> e[N];
inline void dfs(int x,int fa,int &end){
	f[x]=fa;
	dis[x]=dis[fa]+1;
	for(int v:e[x]){if(v==fa)continue;dfs(v,x,end);}
	if(dis[x]>dis[end])end=x;
}
inline void sol(int x,int fa){
	if(!x)return; 
	std::cout<<x<<' ';
	for(int v:e[x]){
		if(v==fa||v==f[x])continue;
		sol(v,x);
		std::cout<<x<<' ';
	}
	if(vis[x])sol(f[x],x);
}
signed main(){
    freopen("in.in","r",stdin);freopen("out.out","w",stdout);
    freopen("combo.in","r",stdin);freopen("combo.out","w",stdout);
    std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
    n=read();for(int i=2;i<=n;++i){int u=read(),v=read();e[u].eb(v);e[v].eb(u);}
    dfs(1,0,st);dfs(st,0,en);
    std::cout<<n-dis[en]<<'\n';int zc=en;
    while(zc)vis[zc]=1,zc=f[zc];
    for(int i=1;i<=n;++i){
    	if(i==st||i==en)continue;
    	int num=0;
    	if(vis[i])num=e[i].size()-2;
    	else num=e[i].size()-1;
    	for(int j=1;j<=num;++j)std::cout<<i<<' ';
    }std::cout<<'\n';
	sol(en,0);
    exit(0);
}