A:

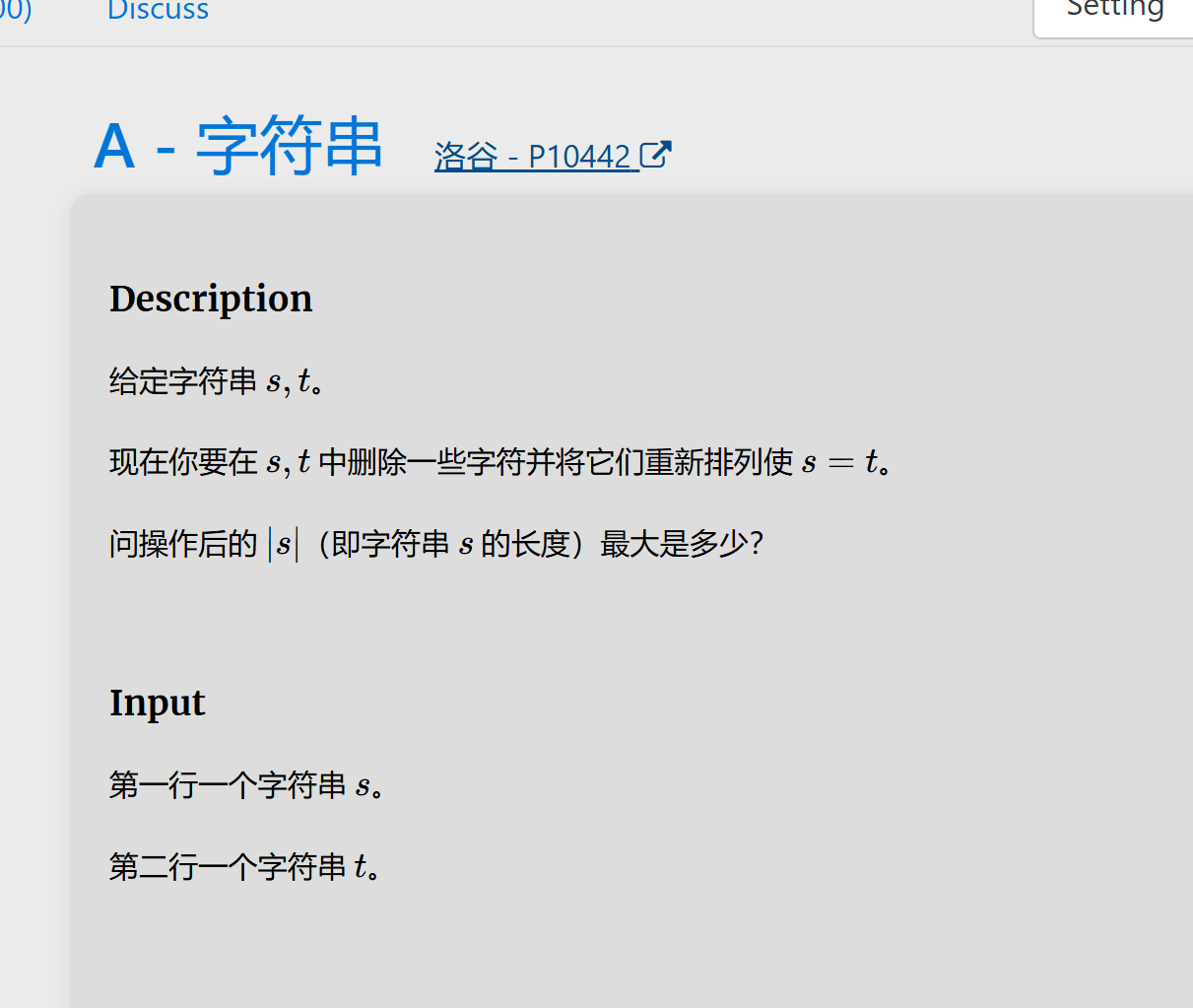
要使s,t相等只要互相删除对方没有的字母即可，即找到a-z字母拥有最少的

#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;

string s1, s2;
int a1[30], a2[30];
void solve(){
	cin >> s1 >> s2;
	for(int i = 0; i < s1.size(); i++){
		int x = s1[i]-'a';
		a1[x]++;
	}
	for(int i = 0; i < s2.size(); i++){
		int x = s2[i]-'a';
		a2[x]++;
	}
	int sum = 0;
	for(int i = 0; i <26; i++) sum+=min(a1[i], a2[i]);
	cout << sum;
}
signed main (){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); 
	int T;
//	cin >> T;
	T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

B:

#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
const int mod = 1e9+7;

int k;
void solve(){
	cin >> k;
	int ret = 7, num=1;
	for(int i = 1; i <= 1e7; i++){
		if(ret%k==0){
			cout<< num ;
			return ;
		}
		ret=ret*10+7; ret%=k;
		num++;
	}
	cout << "-1" ;
}
signed main (){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); 
	int T;
//	cin >> T;
	T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

C:

对于任意两个数求和，即为每个数与之后的前缀和的积的和，注意MOD使用

#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
const int mod = 1e9+7;

int n, a[200010], b[200010];
void solve(){
	cin >> n;
	int sum = 0;
	for(int i = 1; i <= n; i++){
		cin >> a[i];
		b[i] = a[i]+b[i-1];
	}
	for(int i = 1; i < n; i++){
		sum = (sum + (  (a[i]%mod)  *  ((b[n]-b[i])%mod)  ) %mod ) %mod;
	}
	cout << sum%mod;
}
signed main (){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); 
	int T;
//	cin >> T;
	T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

D:
求出每个与i相乘不会大于n的数即可，其值为1到n的i的倍数，即为n/i

#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
const int mod = 1e9+7;

int n;
void solve(){
	cin >> n;
	int num = 0;
	for(int i = 1; i < n; i++){
		num+=(n-1)/i;
	}
	cout << num;
}
signed main (){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); 
	int T;
//	cin >> T;
	T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

E:

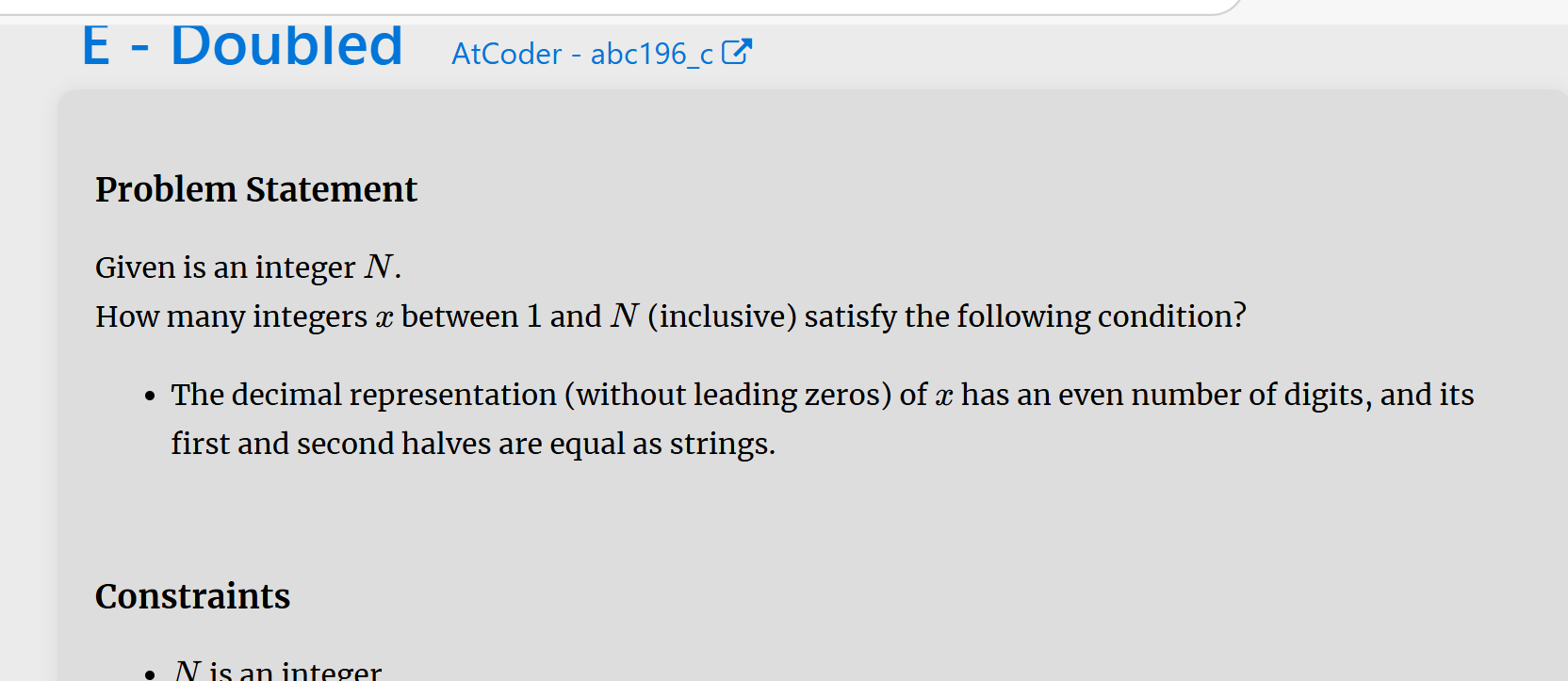
数据范围为1e12，枚举到1到1e6判断该数字是否成立，即将其接一个上去与n比较即可

#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
const int mod = 1e9+7;

int n;
int se(string s){
	s+=s;
	int ret = 0;
	for(int i = 0; i < s.size(); i++){
		ret = ret*10+(s[i]-'0');
	}
	return ret;
}
void solve(){
	cin >> n;
	int num = 0;
	for(int i = 1; i <= 1e7; i++){
		if(n>=se(to_string(i))) num++;
		else break;
	}
	cout << num;
}
signed main (){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); 
	int T;
//	cin >> T;
	T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

F:


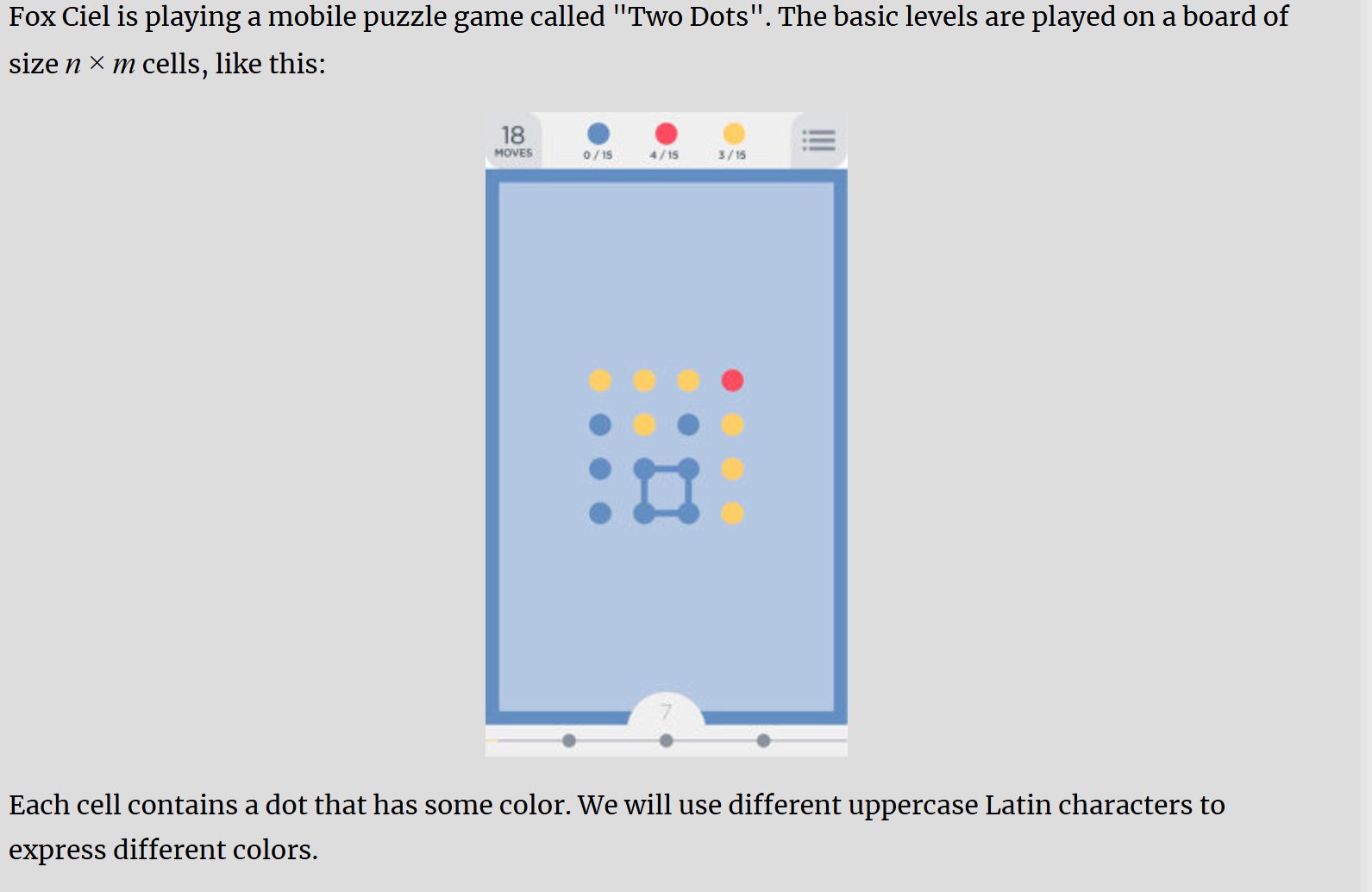
dfs实现，对于一块颜色相同的相连区域，只需要搜索一遍即可，而只要走到颜色相同且已经走过的位置即为成环，注意不能往回走

#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;

int n, m, a[60][60];
int s1[4] = {-1,0,0,1};
int s2[4] = {0,-1,1,0};
char c[60][60];
int p = 0;
void dfs(int x, int y, int lx, int ly){
	if(a[x][y]){
		p = 1;
		return ;
	}
	a[x][y] = 1;
	for(int i = 0; i < 4; i++){
		int nx = x+s1[i];
		int ny = y+s2[i];
		if(nx==lx && ny==ly) continue;
		if(nx>=1 && nx<=n && ny>=1 && ny<=m && c[nx][ny]==c[x][y]){
			dfs(nx, ny, x, y);
		}
		if(p) break;
	}
}
void solve(){
	cin >> n >> m;
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
			cin >> c[i][j];
	
	for(int i = 1; i <= n;i++){
		for(int j = 1; j <= m; j++){
			if(p) break;
			if(a[i][j]==0){
				dfs(i,j,i,j);
			}
			if(p) break;
		}
		if(p) break;
	}
	if(p) cout << "Yes" ;
	else cout << "No";
}
signed main (){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int T;
//	cin >> T;
	T = 1;
	while (T--) {
		solve();
	}
	return 0;
}