POJ3259-Wormholes

GerJCS岛 / 2024-10-22 / 原文

POJ好了（好了后我也经历了崩溃，详间上一个题后面的更新）

继续刷邝斌飞最短路专题

POJ3259

洛谷（翻译贼棒）

可用平台没有这个题

题意给我干缺氧了，鬼翻译真无语，都没看原汁原味的英文读的通顺，洛谷题目里说的农场，农田，地，这仨玩意给我干蒙了，其实农场和农田都是一个。我直接去看poj的英文吧，结合百度翻译，题意如下：

农场主有F个的大农场，每个大农场都各自有N块田地和W个虫洞，对于每个大农场的这些N块田地来说，

既有M条双向路(即无向边)，连接这N块田，（可能存在1号田地到2号田地有很多路的情况，原英文： Two fields might be connected by more than one path. ，你可以把田地想成点）

也有W条单向路的虫洞连接这N块田，（即有向边，原英文： one-way path ，英文题意某田地到某田地的有向路径不存在多条），问你是否存在从某个田地出发走来走去，最后能在出发点之前回到起点。根据第一个样例出发点之前0s回到也是不行的。

数据范围：1<=大农场F<=5、1<=田地N<=500、1<=路M<=2500、1<=虫洞W<=200、1<=虫洞和双向路径长度均是<=10^4

理解完题好懵逼，一想到是最短路就有点思路了

迪杰斯特拉无法处理负边，参考博客，其实只有那个图有用

但我发现不对啊，迪杰斯特拉为啥不能处理负边啊？？如果你以这个想法去理解迪杰斯特拉的话，那之前的那几个题A的都是照抄模板根本没理解算法本质啊，我一个题墨迹半天才A掉，你们直接套模板短时间AC证明根本没理解啊。

之前的几个题虽然没负边，但每次将点加进去后，都不是这个点的最优解，后面沾亲带故的更新会逐渐把最优解更新出来

现在负边也是啊

比如看爹给你举个例子

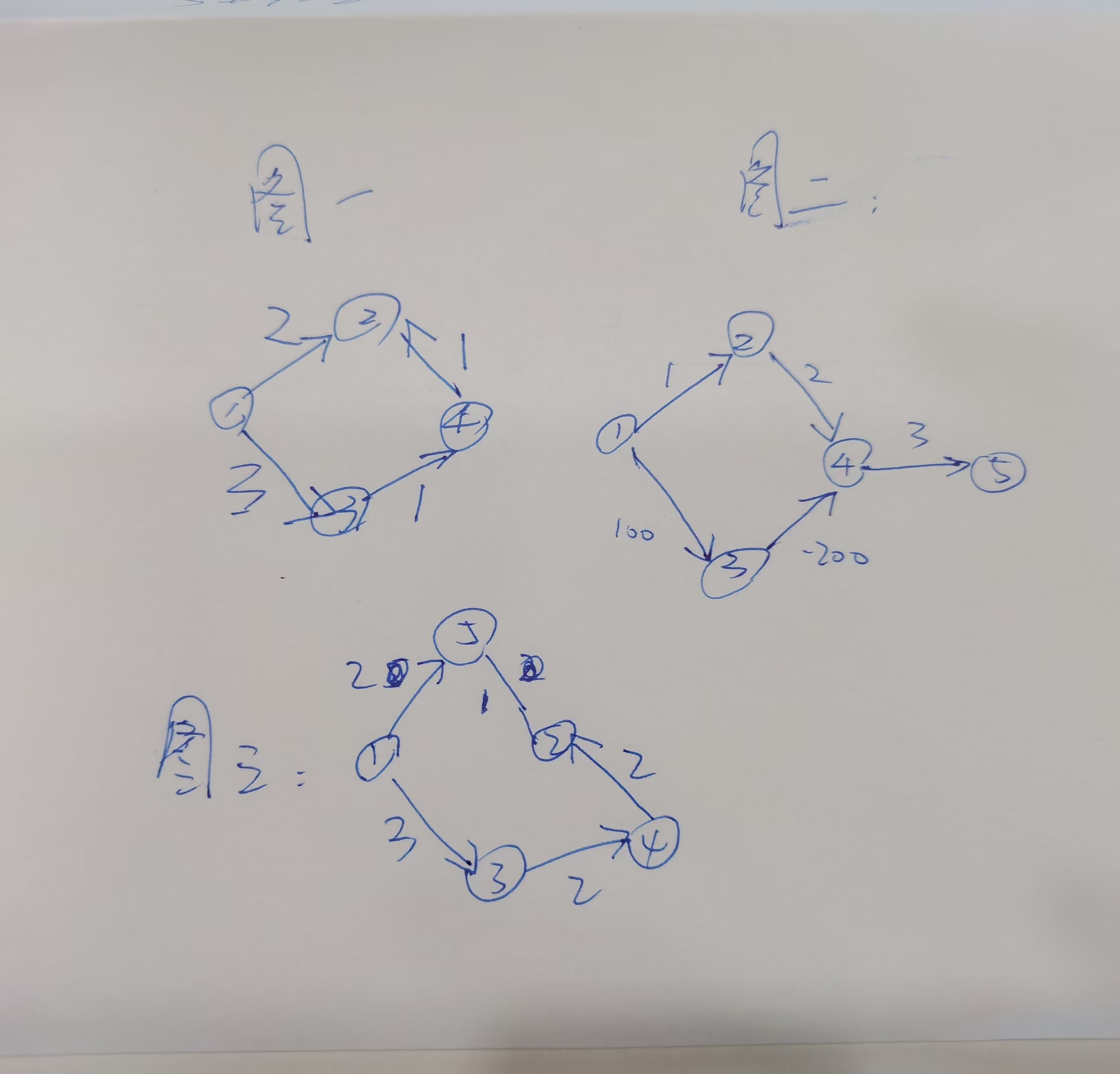
你就瞅图一，新开个标签页，把我这篇文章的链接复制打开，新开的标签拖出来，alt+←分屏看

如果每条路的权值表示这条路能承受的重量的话，假设一段路中各个线段的承重最少的那段，为此段路的最大承重，问你①到②最大承重的最大值，或者说短板最大可以取多少。如果连这句话都读不懂就去把前几道题刷了(Heavy Transportation那个题，md我发现自己写的博客自己回头都不愿意看，q神：想破脑袋想出来的怎么会忘，岛：忘记思路但感觉在)，不过也可能是我没描述清楚

按照迪杰斯特拉，起手①①到自身设置为无穷大(没什么实际意义，只是这样方便写代码)，然后①到所有点memset为0

①①、①②、①③、①④做比较，最大承重为①①是无穷大，①点加进来沾亲带故更新①②和①③距离为2和3，①点滚犊子别再参与之后的比较

①②和①③做比较，最大承重是①③是3，③点加进来，然后更新①④最大承重为1，③点滚犊子别再参与之后的比较

①④和①②做比较，最大承重是①②是2，②点加进来，发现没有可以更新的，然后继续，②滚犊子别再参与后面的比较

然后只有④加进来，做更新发现走④导致①②最大承重为1，之前最大承重是2，所以不更新，①②最大承重是2.

所以你看起初③点加进来了，但他走①③去往②的路径并不是最后的答案，后加进来的②才是。

什么你没考虑这些？你直接就套模板，第一次就找最小了？②加进来就完事了？

那你再看图三，我刚发现其实也行，找最小⑤加进来，更新①②最大承重是1，然后③加进来，更新导致①④最大承重是2，④加进来，更新导致①②最大承重比之前1大，那更新为2，也行。

至此我发现是不是每次不论找最大还是最小都行，那是不是只要顶点距离你有距离，你就可以加进来？反正我加进来导致什么结果只是暂时的，后面有比我更合适的就会更新，于是乎，我用Heavy Transportation那题试了一下，代码简称逆反版本吧，但却可以更加理解算法

首先啊，看好，本应该每次选最大值，然后加进去，下次不再做比较，具体看我之前的博客

这里为了验证猜想，我写每次取最小值看行不行，但注意，初始值怎么设置看松弛那个if里的比较，我想把没更新过的进行更新即松弛，通过小于号，这里因为是永远取短板最大，所以必须用小于号，比你小就更新(不要把松弛和做比较加进去这两件事搞混淆)，那本来没有路的我就要将maxweight用memset成0没得说，但每次比较如果你想找最小的话，0没路如果加进来那毫无意义，因为下一步没法更新，比如数据

那我如果把③因为他没路是0最小就加进来，本来可以通过③更新①④，但这么一整，①④会更新为0没意义，那如果找最小的时候加一个特判只要是没路的0就不算在比较范围内，算了我干脆不找最小了，我直接随机，遍历到谁谁加进来

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<math.h>
 4 #include<iostream>
 5 using namespace std;
 6 int weight[1001][1001];
 7 int maxweight[1001];
 8 int vis[1001];
 9 int thismax;
10 int main()
11 {
12     freopen("data.txt","r",stdin);
13     int t;
14     scanf("%d",&t);
15     int tp=t;
16     while(t--)
17     {
18         memset(weight,0,sizeof(weight));
19         int n,m;
20         scanf("%d%d",&n,&m);
21         memset(maxweight,0,sizeof(maxweight));
22         memset(vis,0,sizeof(vis));
23 
24         int a,b,c;
25         for(int i=0;i<m;i++){
26             scanf("%d%d%d",&a,&b,&c);
27             weight[a][b]=c;
28             weight[b][a]=c;//数据输入完毕
29         }
30         for(int i=1;i<=n;i++)
31             maxweight[i]=weight[1][i];
32         int p;
33         vis[1]=1;
34         for(int i=1;i<=n;i++){
35             for(int j=1;j<=n;j++){
36                 if(vis[j]==0&&maxweight[j]!=0)
37                     p=j;
38             }
39             cout<<"!"<<p<<endl;
40             vis[p]=1;
41             for(int j=1;j<=n;j++){//松弛
42                 if(maxweight[j]<min(maxweight[p],weight[p][j])){
43                     maxweight[j]=min(maxweight[p],weight[p][j]);
44                     if(j==1)
45                         maxweight[p]=maxweight[j];
46                     cout<<p<<" "<<j<<" "<<maxweight[j]<<endl;
47                 }
48             }
49         }
50         cout<<"Scenario #"<<tp-t<<":"<<endl;
51         cout<<maxweight[n]<<endl;
52         cout<<endl;
53     }
54 }

View Code

也WA，但我的思路我觉得没任何问题，对拍好久终于找到了问题

对拍代码

 1 #include<stdio.h>
 2 #include<iostream>
 3 #include<time.h>
 4 using namespace std;
 5 int a;
 6 int b;
 7 int c;
 8 int main(){
 9     srand(time(0) + (unsigned long long)(new char));
10     int n = rand()%5+2;
11     int m = rand()%5+1;
12     int x=rand()%n+1;
13     cout<<"1"<<endl;
14     cout<<n<<" "<<m<<endl;
15     for(int i=0;i<m;i++){
16         a=rand()%n+1;
17         b=rand()%n+2;
18         c=rand()%7+1;
19         cout<<a<<" "<<b<<" "<<c<<endl;
20     }
21 }

View Code

数据

自己画个图，这里当随便进入的时候，如果④点进入了，那他之后不会再进入参与比较，①⑤最大承重就会更新为3，由于④不会再进入且到⑤只有经过④这个点，所以永远无法得到正确答案①③②④⑤最大承重4。那每次找最大就可以完美实现

由此可见，每次找到的并不是最优解只是伪最优，但是向着真最优趋势上走的

吼吼，回过头来发现图三确实不行，确实处理不了负边，参考博客里面说的是对的，这个逼解释的相当完美，处理不了负边跟负边没关系

说服自己了，老老实实去学处理负边的算法　　

好的令人高潮的博客，全网最强，唯一一点这哥们的代码写的太抽象了艹，后面代码还不错，学到了记录路径的小技巧，跟之前搜索里的记录轨迹明显上升了个难度

但写了一半，发现贝尔曼福特算法复杂度是n^3啊，并不是m*n，且没闭环回来的啊，而且是要从任一点开始走

麻痹的写了一半发现这题是不是弗洛伊德啊

抛开算法束缚重新想下：遍历n(500)，对于每个n，比如说n遍历到了2(意思是从2出发看能不能有题意要求的回到2且时间是之前的情况)，不用1举例子是为了防止忘记这次的遍历，那么我从2到任意点的最短距离可以用最短路算法求，但再到2怎么求？原路返？（不太对）继续向前？（那我这到2不是失去了意义），那我是不是再以得到的最短路为新地图，并反向存一遍地图，然后再从2出发再搞一遍最短路作为回程？(再次觉得邝斌题目的阶梯度层次感真好！！)，但感觉怪怪的，有点der儿，兴许哪里会出错，因为并没要求走你，为啥非要走个你，再从你找去顶点2的最短呢？

时间复杂度：边m总共2500*2+200=5200，输入的时候反存图m(想了好久，这个题更加了解反存图的本质了)，遍历的n *（贝尔曼福特n*m + 反存图的贝尔曼n*m），这里n是点的数量，m是边的数量，5组数据，10^10，2s应该不可以（虽然洛谷又写的是1s）

再看我想到的另一种思路：遍历n(500)，对于每个n，比如说n遍历到了2，那我设置一个东西叫影子顶点，再遍历n遍，每一个点到2有如果距离，我就把这距离赋给影子顶点，那么老子只要找从2到影子顶点最短路是不是负数不就好了吗？也没上一个思路那个der儿。实现了首尾位分离

时间复杂度：遍历出发点n *（设置影子顶点也即影子出发点n + 贝尔曼n*m），但设置影子的时候，边总共2500*2+200+500=5700，最后这500是影子顶点产生的最坏情况，5组数据，10^9，2s可以吧。

再去学一下非n^3版本的贝尔曼算法（那篇高潮博客的基础上，潮上加潮），发现遍历n-1遍，里面的遍历不要求顺序，跟弗洛伊德一样，迪杰斯特拉是找当前极值，不能随便将点加入

代码第一次提交

 1 //#include<stdio.h>
 2 #include<iostream>
 3 #include<string.h>
 4 using namespace std;
 5 int D[502];
 6 int u[502];
 7 int v[502];
 8 int edge[2701];
 9 int dir[502][502];//正常500点，会有dir[1][500]，所以开501，再多开一个给影子顶点用
10 int exist[502][502];//仅仅为了优化地图，针对虫洞
11 int F;
12 int n,m,w;
13 int a,b,c;
14 int attach;
15 int p,q;
16 void bellman();
17 int flag=0;
18 int main()
19 {
20     freopen("zhishu.txt","r",stdin);
21     scanf("%d",&F);
22     while(F--){
23         memset(exist,0,sizeof(exist));
24         memset(edge,0x3f,sizeof(edge));
25         memset(dir,0x3f,sizeof(dir));
26         scanf("%d%d%d",&n,&m,&w);
27         for(int i=1;i<=m*2;i++){
28             scanf("%d%d%d",&a,&b,&c);
29             u[i]=a;
30             v[i]=b;
31             edge[i]=c;//真正贝尔曼算法用到的
32             dir[a][b]=c;//为影子顶点准备的
33             exist[a][b]=i;//后面优化边的数量用的
34             i++;
35             u[i]=b;
36             v[i]=a;
37             edge[i]=c;
38             dir[b][a]=c;
39             exist[b][a]=i;
40         }
41         p=0;
42         for(int i=m*2+1;i<=m*2+w-p;i++){
43             scanf("%d%d%d",&a,&b,&c);
44             if(exist[a][b]!=0){//优化边的数量，如果之前有过这条边，但是正数，这次将要输入的是负数，有就把之前的正数用这次的负数覆盖掉，减少边的数量。即某点到某点如果有虫洞，完全可以走虫洞，不走路
45                 edge[exist[a][b]]=-c;//起点终点uv和dir之前已经有了
46                 p++;//相当于这次i作废了，是把之前的覆盖了
47             }
48             else
49             u[i]=a;
50             v[i]=b;
51             edge[i]=-c;
52             dir[a][b]=-c;
53         }
54 //        至此输入结束
55 //        总共表面上输入了m+w条边，m双向，共输入了2m+w条，p记录了重复的边，总共2m+w-p条边
56 //        for(int i=1;i<=2*m+w-p;i++)
57 //            cout<<u[i]<<" "<<v[i]<<" "<<dir[i]<<endl;//测试发现完美实现
58         flag=0;
59         for(int i=1;i<=n;i++){//分别从1、从2、从3...出发，找到就停止
60             if(D[n+1]<0){
61                 flag=1;//找到有可以完成的
62 //                cout<<D[n+1]<<endl;
63                 cout<<"YES"<<endl;
64                 break;
65             }
66             q=2*m+w-p;//目前实际边数
67             attach=0;//如果没有到i的点，附加边就是0，i为顶点
68             memset(D,0x3f,sizeof(D));
69             D[i]=0;
70             for(int j=1;j<=n;j++){
71                 if(dir[j][i]!=0x3f3f3f3f){
72                     edge[++q]=dir[j][i];
73                     u[q]=j;
74                     v[q]=n+1;//影子顶点
75                     attach++;
76                 }
77             }
78             bellman();
79         }
80         if(flag==0)
81             cout<<"NO"<<endl;
82     }
83 }
84 
85 void bellman()
86 {
87     for(int k=1;k<=n;k++){//变量没啥用，纯纯为了使下面操作循环n-1遍，算上影子
88         for(int i=1;i<=(2*m+w-p+attach);i++)
89             if(D[v[i]]>D[u[i]]+edge[i])
90                 D[v[i]]=D[u[i]]+edge[i];
91     }
92 }

View Code

之前说过这种提示不太喜欢，那个下载数据都懒得看转去用POJ了，返回的是WA

怎么感觉被模板整思维定势了呢，这里貌似并不只是n-1趟就可以了，是往返啊，而且好像直接也不用镜子顶点，搞对遍历的趟数貌似就可以了艹。

感觉是2倍的n，依旧WA，不想看洛谷分数是不是接近了，我这么弱还活在世界上真的对不起，艹怒了，就硬调，

###：

经历和阅历让我杀伐果断，但图书馆学习+心性始终无法↓，表面又很。妖朋友圈，江湖气+书生气。q神虽然不看代码，洛谷看，但我之前夏天群武理北大那个，我也给他找bug装逼，找bug再装女

19BUPT考研纸盒电梯场景刚学队列 

不看题解的好处

1、踩过坑所有办法都想一遍，找到正确的解题办法，不然永远无法自己想到解题办法

2、题解的一个简简单单的结论，背后有许多思考，没亲自走过这些思考过程，这个结论根本看不懂，就算看懂了下次同样类型的根本想不到，因为很多坑其实相通

View Code

###：风格不错的博客

###：小知识回顾：n个点最多n(n-1)/2条边