Codeforces Round 978 (Div. 2) C. Gerrymandering 轮廓DP

nannandbk / 2024-10-19 / 原文

Codeforces Round 978 (Div. 2) C轮廓DP

C. Gerrymandering

思路：考虑有哪些情况呢？

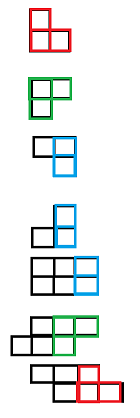
发现结尾只有三种情况，0.平的，1.上凸，2.下凸。

那么每一种后面能出现什么呢？

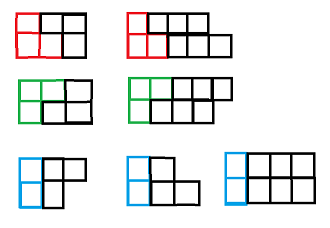
这样看起来就好写啦。

// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
ll a[N],b[N];
ll dp[N][3];
 
 
 
int main()
{
    ios::sync_with_stdio(false);   cin.tie(nullptr), cout.tie(nullptr);
    int t; cin>>t;
    while(t--)
    {
        int n; cin>>n;
        for(int i = 1;i <= n; i++){
            char x; cin>>x;
            a[i] = (x=='A');
        }
        for(int i = 1;i <= n; i++){
            char x; cin>>x;
            b[i] = (x=='A');
        }
 
        memset(dp,128,sizeof(dp));
         
        dp[0][0] = 0;
 
        for(int i = 1;i <= n; i++)
        {
           if(i >= 3)
           {
                dp[i][0] = max(dp[i][0],dp[i-3][0]+((a[i]+a[i-1]+a[i-2])>=2)+((b[i]+b[i-1]+b[i-2])>=2));//###
                                                                                                        //###
 
                dp[i][1] = max(dp[i][1],dp[i-3][1]+((a[i]+a[i-1]+a[i-2])>=2)+((b[i-1]+b[i-2]+b[i-3])>=2));//.###
                                                                                                          //###.
 
                dp[i][2] = max(dp[i][2],dp[i-3][2]+((a[i-1]+a[i-2]+a[i-3])>=2)+((b[i]+b[i-1]+b[i-2])>=2));//###.
                                                                                                          //.###
           }
 
           if(i >= 2)
           {
                dp[i][1] = max(dp[i][1],dp[i-2][0]+((a[i]+a[i-1]+b[i-1])>=2));//##
                                                                              //#.
 
                dp[i][2] = max(dp[i][2],dp[i-2][0]+((a[i-1]+b[i]+b[i-1])>=2));//#.
                                                                              //##
           }
 
           dp[i][0] = max(dp[i][0],dp[i-1][2]+((a[i-1]+a[i]+b[i])>=2));//##
                                                                       //.#
 
           dp[i][0] = max(dp[i][0],dp[i-1][1]+((a[i]+b[i]+b[i-1])>=2));//.#
                                                                       //##
 
 
 
             
     }
      cout<<dp[n][0]<<"\n";
 
    }
    return 0;
}