yukiの数论笔记（连载中！）

nagato--yuki / 2024-10-11 / 原文

前言

最近被数论这东西搞的烦死了，所以写篇笔记整理一下
貌似所有$gcd$和$mod$都是斜体不是正体，懒得改了$qwq$
注：此笔记尚未写完，还在连载中（更新进度：扩展卢卡斯定理）

Chapter #1 数论基础

1.1 整除

定义：有两个数 $a,b$，若有 $a=kb$，则可说 $a$ 可被 $b$ 整除，记作 $b|a$

1.1.1 整除的基本性质

若 $a|b,b|c$，则 $a|c$
$a|b$ 且 $a|c$ 等价于 $\forall x$ 和 $y$，有 $a|(b*x+c*y)$（$\forall$：对于任意的）
设 $m \neq 0$，那么 $a|b$ 等价于 $(m*a)|(m*b)$
设整数 $x$ 和 $y$ 满足下式：$a*x+b*y=1$，且 $a|n, b|n$，那么 $(a*b)|n$
证明：
$~~~~~~~~\because a|n, b|n$
$~~~~~~~~$由第三条性质得 $(a*b)|(n*b)$ 且 $(b*a)|(n*a)$
$~~~~~~~~$由第二条性质得 $(a*b)|(a*n*x+b*n*y)$
$~~~~~~~~a*n*x+b*n*y=n*(a*x+b*y)=n*1=n$
$~~~~~~~~\therefore (a*b)|n$

1.1.2 约数与倍数

$~~~~~~~~$定义：若$a|b$，则称 $a$ 是 $b$ 的约数（或因数），$b$ 是 $a$ 的倍数

1.2 最大公约数与最小公倍数

1.2.1 公约数的定义

如果一个整数同时是几个整数的约数，称这个整数为它们的公约数。公约数中最大的称为最大公约数(Greatest Common Divisor
(GCD))。

一般地，当两个数 $a,b$ 的最小公倍数为 $1$ 时，我们就称这两个数互质。

1.2.2 公倍数的定义

如果一个整数同时是几个整数的倍数，称这个整数为它们的公倍数。公倍数中最大的称为最小公倍数(Least Common Multiple
(LCM))。

我们怎样求两个数的最小公倍数呢？

这里有一个方法：辗转相除法。

1.2.3 辗转相除法的原理

原理：$gcd(x,y)=gcd(x,x-y)$

证明如下：
设 $a=gcd(x,y),x=am,y=an$

$\therefore x-y=a(m-n)$

$\therefore gcd(x,y)=gcd(x,x-y)$

$\therefore gcd(x,y)=gcd(x,x\ mod\ y)$

代码如下：

int gcd(int x,int y)
{
    if(y==0)return x;
    return gcd(y,x%y);
}

那么最小公倍数又怎么求呢？
我们假设两个数 $a,b$，将它们质因数分解：
$a={k_1}^{a_1}*{k_2}^{a_2}*\cdots*{k_n}^{a_n}$

$b={k_1}^{b_1}*{k_2}^{b_2}*\cdots*{k_n}^{b_n}$

则
$gcd(a,b)={k_1}^{min(a_1,b_1)}*{k_2}^{min(a_2,b_2)}*\cdots*{k_n}^{min(a_n,b_n)}$

$lcm(a,b)={k_1}^{max(a_1,b_1)}*{k_2}^{max(a_2,b_2)}*\cdots*{k_n}^{max(a_n,b_n)}$

不难看出

$gcd(a,b)*lcm (a,b)=a*b$

于是

$lcm(a,b)=\frac{a*b}{gcd(a,b)}$

代码如下：

int lcm(int x,int y)
{
    return x*y/gcd(x,y);
}

1.3 同余

同余式是数论的基本概念之一，设$m$是给定的一个正整数，$a,b$ 是整数，若满足 $m|(a-b)$，则称 $a$ 与 $b$ 对 $mod$ $m$ 同余，记为 $a≡b(mod$ $m)$。
摘自百度百科

1.3.1 同余的基本性质

自反性：$a \equiv a(mod$ $m)$（这个还是很容易的吧）
对称性：若 $a \equiv b(mod$ $m)$，则 $b \equiv a(mod$ $m)$
传递性：若 $a \equiv b(mod$ $m)$，$b \equiv c(mod$ $m)$，则 $a \equiv c(mod$ $m)$
同加性：若 $a \equiv b(mod$ $m)$，则 $a+c \equiv b+c(mod$ $m)$
这也是很容易证明的，设 $a-b=km,$ 则有 $(a+c)-(b+c)=km \Rightarrow a+c \equiv b+c(mod$ $m)$
同乘性(1)：若 $a \equiv b(mod$ $m)$，则 $a*c \equiv b*c(mod$ $m)$（证明同上）
同乘性(2)：若 $a \equiv b(mod$ $m)$，$c \equiv d(mod$ $m)$，则 $ac \equiv bd(mod\ m)$
证明：设 $xm=a-b$，$ym=c-d$
则 $ac=(xm+b)(ym+d)=(xy+x+y)m+bd$
$ac-bd=(xy+x+y)m$
$\therefore ac \equiv bd(mod\ m)$
同幂性：若 $a \equiv b(mod$ $m)$，则 $a^c \equiv b^c(mod$ $m)$
把其看成多个同余的数相乘，运用 同乘性(2)
同除性(1)：若 $ac\equiv bc(mod\ m)$ 且 $gcd(c,m)=1$，则 $a\equiv b(mod\ m)$
证明：$m\mid ac-bc$
$m\mid c(a-b)$
$\because gcd(c,m)=1$，即 $c$ 与 $m$ 没有除$1$外的公因数
即使除去 $c$，仍然有 $m|a-b$
同除性(2)：若 $ac\equiv bc(mod\ m),d=gcd(c,m)$，则 $a\equiv b(mod\ \frac{m}{d})$
证明：$\because m\mid c(a-b)$
$\therefore \frac{m}{d}\mid \frac{c}{d}(a-b)$
除去 $c$ 相当于只是除去了 $c$ 与 $m$ 的最大公因数
$\frac{m}{gcd(c,m)}$ 还是能整除 $a-b$ 的

这里还有几个关于同余的推论：
（1）
$a*b\ mod\ k=(a\ mod\ k)\ *\ (b\ mod\ k)\ mod\ k$
证明：运用同乘性(1)
和 同乘性(2) 即可

（2） 若 $a\ mod\ p=x$，$a\ mod\ q=x$，且 $p,q$ 互质，则 $a\ mod\ p*q=x$
证明：
$\because a\ mod\ p=x,a\ mod\ q=x$
$\therefore $ 一定存在整数$s,t$，使$a=s*p+x，a=t*q+x$
$\therefore s*p=t*q$
$\because $ $p,q$互质，即$p,q$含有互不相同的质因子
$\therefore s$一定有$q$的质因子
$\therefore$ 一定存在整数$r$，使$s=r*q$
$\therefore a=r*p*q+x$，即$a\ mod\ p*q=x$

1.4 同余类与剩余系

这里大部分摘自OI WIKI，只不过那上面讲的太史了，所以写成了我能看懂的样子。

1.4.1 同余类的定义

对于一个非零整数 $m$，我们选择一个数 $a$，则有 $a\equiv a+m\equiv a+2m\equiv \cdots \equiv a+km(mod\ m)$，其中 $k$ 为整数。

我们这些模 $m$ 意义下互相同余的数，放到一个集合里，就可以称这个集合为含有整数 $a$ 的模 $m$ 的同余类，用 $a\ mod\ m$ 来表示。

例如有一个模数 $7$，则 $2,9,16,\cdots$ 在一个同余类里，用 $2\ mod\ 7$ 来表示，也可以用 $9\ mod\ 7$ 来表示。

不难证明，对于模数 $m$，一共有 $\lvert m \rvert$ 个同余类。

1.4.2 剩余系的定义

由抽屉原理得，对于一个模数 $m$，任取 $m+1$ 个数，必然有两个数模 $m$ 同余。（这里很容易想吧）

同时，也存在 $m$ 个数，模 $m$ 互不同余。

我们把这 $m$ 个数，称为模 $m$ 的一个完全剩余系。

例如 $m=3$ 时，$\{1,2,3\}$ 是模 $m$ 的完全剩余系，$\{1,5,9\}$ 也是。

这里还有几个特殊的完全剩余系：

最小非负（完全）剩余系：$0,\dots,m-1$；
最小正（完全）剩余系：$1,\dots,m$；
绝对最小（完全）剩余系：$-\lfloor m/2\rfloor,\dots,-\lfloor -m/2\rfloor-1$；
最大非正（完全）剩余系：$-m+1,\dots,0$；
最大负（完全）剩余系：$-m,\dots,-1$。

1.4.3 剩余系的复合

这里假设 $Z_{m1},Z_{m2}$ 分别为 $m_1,m_2$ 的完全剩余系，$m=m_1*m_2$，那么我们能用 $Z_{m1},Z_{m2}$ 来表示 $Z_m$ 吗？

我们将集合间的运算以如下方式表示（:=意为“定义为”）：

$Z+a:=\{a+z:z\in Z\}$
意为将 $a$ 与集合 $Z$ 中任一元素相加。
$Za:=\{a*z:z\in Z\}$
意为将 $a$ 与集合 $Z$ 中任一元素相乘。
$Z_1+Z_2:=\{z_1+z_2:z_1\in Z_1,z_2\in Z_2\}$
意为将 $Z_1$ 中任一元素与集合 $Z_2$ 中任一元素相加。
$Z_1Z_2:=\{z_1*z_2:z_1\in Z_1,z_2\in Z_2\}$
意为将 $Z_1$ 中任一元素与集合 $Z_2$ 中任一元素相乘。

然后，对于 $Z_m$，我们可以这样表示：
$Z_m=Z_{m1}+m_1Z_{m2}$

例如，假设 $m_1=2,m_2=3$，$2$ 的完全剩余系 $Z_1=\{0,1\}$，$3$ 的完全剩余系 $Z_2=\{0,1,2\}$，用上面的式子可以表示 $6$ 的完全剩余系 $Z=\{0,1,2,3,4,5\}$。

下面给出证明。

对于 $Z_2$，显然我们可以这样表示：$Z_2=\{k_1m_2+0,k_2m_2+1,\cdots,k_{m_2}m_2+(m_2-1)\}$（其中 $k_i$ 为整数）。

这时，我们把 $Z_2$ 中的每个元素乘上 $m_1$，$Z_2$ 就变成了这样：$\{k_1m_2*m_1+0*m_1,\cdots,k_{m_2}m_2*m_1+(m_2-1)*m_1\}$

对集合中的任一元素对 $m$ 取模，因为 $m_1*m_2=m$，所以我们可以得到一个新集合 $A=\{0,m_1,2m_1,\cdots,(m_2-1)*m_1\}$

还是用刚才的表示方法表示 $Z_1:\{k_1m_1+0,k_2m_1+1,\cdots,k_{m_1}m_1+(m_1-1)\}$

对于 $Z_1$ 中的第一个元素，加上 $A$ 中的任一元素，再对 $m$ 取模，得到一个新集合。实际上，这个新集合就等于 $A$。

因为对于 $m_2$ 的一个完全剩余系 $\{0,1,\cdots,m_2-1\}$，加上 $1$ 之后，原集合的 $0$ 变成 $1$，$m_2-1$ 变成 $0$，依此类推，还是原来的集合。

前面的新集合也是如此，只不过乘了 $m_1$，模数变成 $m_1*m_2$ 而已，本质上仍然不变。

对于 $A$ 中的第二个元素，我们也这么操作，能得到一个新集合 $\{1,m_1+1,\cdots,(m_2-1)*m_1+1\}$。

对于剩下的元素，我们都这样操作。最后，把这些新集合合起来，我们能得到一个大集合：$\{0,1,2,\cdots,m-1\}$。这正好是$m$的完全剩余系 $Z$。

综上所述，我们就能得到一个式子：

\[Z_m=Z_{m1}+m_1Z_{m2} \]

如果 $m$ 为 $3$ 个数相乘，求 $Z_m$ 的时候只要先把 $Z_{m_1*m_2}$ 求出来，再求 $Z_m$ 就行了。多个数相乘的情况依此类推。

对于 $k$ 个数相乘的情况，有如下式：

\[Z_m=Z_{m_1}+m_1Z_{m_2}+m_1m_2Z_{m_3}+\cdots +m_1m_2\cdots m_{k-1}Z_{m_k} \]

即：

\[Z_m=\sum_{i=1}^{k}\bigg(\prod_{j=1}^{i-1}m_j\bigg )Z_{m_i} \]

Chapter #2 同余方程（一）

2.1 扩展欧几里得算法

对于两个数 $a,b$，我们怎样找出不定方程 $ax+by=gcd(a,b)$ 的一组通解呢？

我们发现，在进行辗转相除法的时候，最后一步总是有

$a_0=gcd(a,b),b_0=0 \Rightarrow x=1,y=0$

这玩意是不是也能倒推回去呢？

在c++中，$a\ mod\ b=a-a/b*b$（此处为整除）

将 $ax+by=gcd(x,y)$ 转为 $bx+(a-a/b*b)y=gcd(x,y)$

$bx+(a-a/b*b)y=bx+ay-(a/b*b)y=ay+b(x-a/b*b)$

由此见得

上一步的 $x=$ 下一步的 $y$

上一步的 $y=$ 下一步的 $x-a/b*b$

这样，我们就可以在递归的时候轻松倒推了

代码如下：

#include<bits/stdc++.h>
using namespace std;
int a,b,c,x,y,ans;
int exgcd(int a,int b,int &x,int &y)
{
    int ret,tmp;
    if(!b)
    {
        x=1,y=0;
        return a;
    }
    ret=exgcd(b,a%b,x,y);
    tmp=x,x=y,y=tmp-a/b*y;
    return ret;
}
int main()
{
    cin>>a>>b>>c;
    ans=exgcd(a,b,x,y);
    cout<<x<<' '<<y;
    return 0;
}

2.2 裴蜀定理

2.2.1 内容

对于任意两个数 $a,b$，设 $d=gcd(a,b)$。则关于未知数 $x$ 和 $y$ 的一元一次不定方程 $ax+by=m$ 有整数解
$(x,y)$ 当且仅当 $m$ 是 $d$ 的整数倍。

2.2.2 证明

在上一章内容中，我们已经找到了一组通解 $(x_0,y_0)$ 满足 $ax_0+by_0=d=gcd(a,b)$

设 $m=pd$

则 $pd=p(ax_0+by_0)=a*px_0+b*py_0$

解得

\[ \begin{cases} x=px_0 \\ y=py_0 \end{cases} \]

很明显，对于 $d$ 的任意倍数 $m$，方程 $ax+by=m$ 都有一组确定的解。

那么我们如何证明，当 $m\ mod\ d\not=0$ 时，方程 $ax+by=m$ 无法找到一组确定的整数解呢？

我们将方程两边同除以 $d$，得到一个方程：

$\frac{a}{d}x+\frac{b}{d}y=\frac{m}{d}$

显然 $\frac{a}{d}$ 和 $\frac{b}{d}$ 为整数，但 $\frac{m}{d}$ 不是

一个整数加另一个整数，怎么会得到一个分数呢？

所以命题成立，则裴蜀定理得到证明。

2.3 求解二元一次不定方程

有了上面这些知识，相信我们有足够能力解决基本的二元一次不定方程 $ax+by=c$ 了

首先，我们求出 $d=gcd(a,b)$

若 $d \nmid\ c$，则方程无解

由上一章，我们先找到一组通解 $(x_0,y_))$

则方程的任一解可表示为

对任一整数 $t$

\[\left\{ \begin{aligned} x=x_0+\frac{b}{d}*t \\ y=y_0-\frac{a}{d}*t \end{aligned} \right. \]

证明：
$ax+by=a(x_0+\frac{b}{d}*t)+b(y_0-\frac{a}{d}*t)=ax_0+by_0=c$

模板代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,a,b,c,x,y;
ll exgcd(ll a,ll b,ll &x,ll &y){
    ll ret,tmp;
    if(b==0){
        x=1,y=0;
        return a;
    }
    ret=exgcd(b,a%b,x,y);
    tmp=x,x=y,y=tmp-a/b*y;
    return ret;
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n;
    while(n--){
        cin>>a>>b>>c;
        ll gcd=exgcd(a,b,x,y);
        if(c%gcd!=0){
            cout<<-1<<endl;
            continue;
        }    
        ll x0=c/gcd*x,y0=c/gcd*y,k0,k1;
        a/=gcd,b/=gcd;
        if(x0<=0)k0=x0/b*-1+1;
        else{
        	if(x0%b==0)k0=x0/b*-1+1;
        	else k0=x0/b*-1;
		}
		if(y0<=0)k1=y0/a-1;
		else{
			if(y0%a==0)k1=y0/a-1;
			else k1=y0/a;
		}
		if(k1<k0)cout<<x0+k0*b<<' '<<y0-k1*a<<endl;
		else
			cout<<k1-k0+1<<' '<<x0+k0*b<<' '<<y0-k1*a<<' '<<x0+k1*b<<' '<<y0-k0*a<<endl;
    } 
    return 0;
}

2.4 逆元

2.4.1 定义

一个线性同余方程 $ax\equiv 1\ (mod\ b)$，且 $gcd(a,b)=1$，则称 $x$ 为 $a\ mod\ b$ 的逆元，记作 $a^{-1}$。（看上去有点难理解，把它当作数论中的倒数就行了）

若想要计算 $(a/b)%p$，就相当于计算 $a*b^{-1}(mod\ p)$，之后计算组合数取模时就是这样计算的。

2.4.2 逆元的求法

这里介绍几个求逆元的方法。

1.扩展欧几里得算法

$\because ax\equiv 1\ (mod\ b)$
$\therefore b\mid ax-1$
然后我们就可以转化为不定方程 $ax+by=1$，用扩展欧几里得算法就可以求出来了。

2.线性求逆元法

首先，设 $1^{-1}\equiv 1(mod\ p)$

我们求 $i\ mod\ p$ 的逆元时，先设 $p$ 除以 $i$ 等于 $k$ 余 $r$，即 $p=k*i+r(r<i,1<i<p)$
在模$p$意义下，
明显看出，$k*i+r\equiv 0(mod\ p)$
两边同乘 $i^{-1},r^{-1}$，得：
$k*r^{-1}+i^{-1}\equiv 0$
$i^{-1}\equiv -k*r^{-1}$
$i^{-1}\equiv-[\frac{p}{i}]*(p\ mod\ i)^{-1}$（$[]$为取整符号）
于是，我们就可以从前面推出当前的逆元了。

代码如下：

A[i]=(p-p/i)*A[p%i]%p;
//等价于A[i]=-(p/i)*A[p%i];

3.快速幂法
要求 $b$ 为素数。
前置知识：费马小定理。建议学完之后再来看这里。

$gcd(a,b)=1$
$\therefore a^{b-1}\equiv1(mod\ b)$（费马小定理）
$\because ax\equiv1(mod\ b)$
$\therefore ax\equiv a^{b-1}(mod\ b)$
$\therefore x\equiv a^{b-2}(mod\ b)$

然后用快速幂求就行了。

2.5 中国剩余定理

今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？
——《孙子算经》

用现代语言翻译一下上面的话：

求出以下同余方程组的解：

\[\left\{ \begin{aligned} x_0\equiv2(mod\ 3)\\ x_0\equiv3(mod\ 5)\\ x_0\equiv2(mod\ 7) \end{aligned} \right. \]

怎样求出这个方程的解呢？
首先，我们先把这三个方程的解求出来：

\[\left\{ \begin{equation} \begin{aligned} x_1\equiv1(mod\ 3)\\ x_1\equiv0(mod\ 5)\\ x_1\equiv0(mod\ 7) \end{aligned} \end{equation} \right. \]

\[\left\{ \begin{equation} \begin{aligned} x_2\equiv0(mod\ 3)\\ x_2\equiv1(mod\ 5)\\ x_2\equiv0(mod\ 7) \end{aligned} \end{equation} \right. \]

\[\left\{ \begin{equation} \begin{aligned} x_3\equiv0(mod\ 3)\\ x_3\equiv0(mod\ 5)\\ x_3\equiv1(mod\ 7) \end{aligned} \end{equation} \right. \]

对于第一个方程，显然 $x_1$ 为 $7$ 和 $5$ 的公倍数。
则设 $x_1=35y$
$\therefore 35y\equiv1(mod\ 3)$
扩展欧几里得算法解得一个解 $y=2$，则 $x_1=70$

同理，对 $(2)$，解得 $x_2=21$。对 $(3)$，解得 $x_3=15$。

然后，根据同余的基本性质，可以得到

\[\left\{ \begin{aligned} 2x_1\equiv2(mod\ 3)\\ 3x_2\equiv3(mod\ 5)\\ 2x_3\equiv2(mod\ 7) \end{aligned} \right. \]

最后解得一个解 $x_0=2x_1+3x_2+2x_3=233$

随后我们找出通解，设 $m=lcm(3,5,7)=105$

$\therefore x=x_0+m*k$（$k$为整数）

这样，我们就找出上述方程的解了。

综上所述，对于一个一元线性同余方程组：

\[ \begin{cases} x_1\equiv a_1(mod\ b_1)\\ x_2\equiv a_2(mod\ b_2)\\ x_3\equiv a_3(mod\ b_3)\\ \vdots\\ x_n\equiv a_n(mod\ b_n) \end{cases} \]

$($其中$b_1$~$b_n$互质$)$

我们整理出如下做法:

$(1)$ 求出所有模数的积：

$d=b_1*b_2*\cdots*b_n=\prod \limits_{i=1}^nb_i$

$(2)$ 在上文，我们在求解第 $i$ 个方程的时候是求除 $a_i$ 外所有数的最小公倍数，这里模数互质，所以只要算出 $\frac{d}{a_i}$ 就行了，这里记作 $m_i$。

$(3)$ 对于方程 $m_i*y\equiv1(mod\ b_i)$，我们发现 $y$ 就是 $m_i\ mod\ b_i$ 意义上的逆元，算出这个逆元，我们记作 $m_i^{-1}$。

$(4)$ 所以 $x_i=m_i*m_i^{-1},x_0=x_1+x_2+\cdots+x_n=\sum \limits_{i=1}^nx_i=\sum \limits_{i=1}^nm_i*m_i^{-1}$。

$(5)$ 算出 $k=gcd(b1,b2,\cdots,b_n),x=x_0+k*r$，其中 $r$ 为整数。

模板代码如下:

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,a[20],b[20],cnt=1,x,y,f[100010],ans;
void gcd(ll a,ll b,ll &x,ll &y)
{
    ll tmp;
    if(b==0)
    {
        x=1,y=0;
        return;
    }
    gcd(b,a%b,x,y);
    tmp=x,x=y,y=tmp-a/b*y;
    return;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i]>>b[i];
        cnt*=a[i];
    }
    for(int i=1;i<=n;i++)
    {
        ll c=cnt/a[i];
        x=0,y=0;
        gcd(c,a[i],x,y);
        if(x<0)x+=a[i];
        ans+=b[i]*c*x;//gcd(c,b[i])=1
    }
    cout<<ans%cnt;
    return 0;
}

几百年前，宋朝数学家秦九韶于 1247 年《数书九章》卷一、二《大衍类》便对这类问题做出了完整系统的解答。这便是中国剩余定理（Chinese remainder theorem,CRT）。

很遗憾，中国剩余定理并不能解决模数不互质时的情况。

为什么呢？

因为如果模数不互质，前文求出的 $m_i$ 就可能与 $b_i$ 不互质。

根据裴蜀定理，$gcd(m_i,b_i)>1$，$m_i*y\equiv1(mod\ b_i)$ 就求不出来解。

这时，我们就需要扩展中国剩余定理（EXCRT） 的帮助了。

2.6 扩展中国剩余定理

大部分摘自这里

中国剩余定理有个缺陷，就是只适用于模数互质时的情况。所以，我们要扩展一下。

单纯在中国剩余定理上修修改改有点难度，我们尝试换个方法。

对于一个一元线性同余方程：

\[ \begin{cases} x_1\equiv a_1(mod\ b_1)\\ x_2\equiv a_2(mod\ b_2)\\ x_3\equiv a_3(mod\ b_3)\\ \vdots\\ x_n\equiv a_n(mod\ b_n) \end{cases} \]

我们假设 $M_i$ 为 $lcm(b_1,b_2,\cdots,b_i)$，前 $i$ 个方程的一个解为 $x_i$

则有 $M_{i+1}=M_i*(b_{i+1}/gcd(M_i,b_{i+1}))$

又有整数 $t$ 使得 $x_{i+1}=x_i+t*M_i$

$\because x_{i+1}\equiv a_{i+1}(mod\ b_{i+1})$

$\therefore x_i+t*M_i\equiv a_{i+1}(mod\ b_{i+1})$

$\therefore t*M_i\equiv a_{i+1}-x_i(mod\ b_{i+1})$

将 $t$ 设成未知数，那这不就是一个简单的同余方程吗？

我们把 $t$ 解出来就行了，注意判断 $gcd(M_i,b_{i+1})$ 是否整除 $a_{i+1}-x_i$，若不能整除，则方程无解。

模板代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,a[100010],b[100010],ans,lcm,x,y;
ll quickmul(ll a,ll b,ll mod)
{
    //这里有一个龟速乘，是因为防止上溢
    //同时模板要求最小正整数解，这里方便取模
    ll ret=0,tmp=a;
    while(b)
    {
        if(b&1==1)
            ret=(ret+tmp)%mod;
        tmp=(tmp+tmp)%mod;
        b>>=1;
    }
    return ret%mod;
}
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    ll ret,tmp;
    if(b==0)
    {
        x=1,y=0;
        return a;
    }
    ret=exgcd(b,a%b,x,y);
    tmp=x,x=y,y=tmp-a/b*y;
    return ret;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>b[i]>>a[i];
    ans=a[1],lcm=b[1];
    for(int i=2;i<=n;i++)
    {
        ll c=(a[i]+(b[i]-ans%b[i]))%b[i];//这里是为了防止负数
        ll gcd=exgcd(lcm,b[i],x,y);
        x=quickmul(x,c/gcd,b[i]/gcd);
        //这里mod b[i]/gcd是为了取最小正整数解，同时防止上溢
        ans+=x*lcm;
        lcm*=b[i]/gcd;
        ans=(ans%lcm+lcm)%lcm;//防止负数
    }
    cout<<(ans%lcm+lcm)%lcm;
    return 0;
}

Chapter #3 素数（一）

3.1 素数的定义

对于一个数 $m$，如果其除了 $1$ 和 $m$ 外没有其他因数，则称这个数为素数。

特别地，$1$ 和 $0$ 不是素数。

3.2 既约剩余系

3.2.1 定义

对于正整数 $m$ 的一个完全剩余系 $Z_m$，我们把 $Z_i($ 满足 $gcd(Z_i,m)=1)$都拎出来，放到一个集合里，这个集合就叫 $m$ 的既约剩余系，记作 $Z^*_m$。

例如 $8$ 的一个既约剩余系 $\{1,3,5,7\}$，$9$ 的一个既约剩余系 $\{1,2,4,5,7,8\}$，等等。

3.2.2 既约剩余系的复合

当 $m=m_1*m_2$ 且 $gcd(m_1,m_2)=1$ 时，$Z^*_m$ 可以用 $Z^*_{m_1}$ 和 $Z^*_{m_2}$ 这样表示：

\[Z^*_m=m_2Z^*_{m_1}+m_1Z^*_{m_2} \]

举个例子：假设 $m_1=3,m_2=5$，$Z^*_{m_1}=\{1,2\},Z^*_{m_2}=\{1,2,3,4\}$，用上面的式子可以求出 $Z^*_m=\{8,11,13,14,16,17,19,22\}$。

下面给出证明。

我们假设有正整数 $x,y$ 满足 $m_1x+m_2y=m_0($ 满足 $m_0\in Z^{*}_m\ )$，$A=m_2Z^*_{m_1}+m_1Z^*_{m_2}$。

$1.$ 证明 $Z^{*}_m\subseteq A$

$gcd(m_1x+m_2y,m_1m_2)=gcd(m_1x+m_2y,m_1)=gcd(m_1x+m_2y,m_2)=1$（易证）
$gcd(m_1x+m_2y,m_1)=gcd(m_2y,m_1)=1$（辗转相除）
$gcd(m_2y,m_1)=gcd(y,m_1)=1$（易证）

同理可得$gcd(x,m_2)=1$，于是有$x\in Z^{*}_{m_2},y\in Z^{*}_{m_1}$，$Z^{*}_m\subseteq A$。

$2.$证明$A\subseteq Z^{*}_m$

设$m_0(m_0\in A)=xm_1+ym_2$，且$x\in Z^{*}_{m_2},y\in Z^{*}_{m_1}$
则$gcd(xm_1+ym_2,m_1)=gcd(ym_2,m_1)$（辗转相除）$=gcd(y,m_1)=1$（易证）
同理，$gcd(xm_1+ym_2,m_2)=1$

所以，$gcd(xm_1+ym_2,m_1m_2)=1$，即$A\subseteq Z^{*}_m$。

综上所述，$A= Z^{*}_m$，即

\[Z^*_m=m_2Z^*_{m_1}+m_1Z^*_{m_2} \]

3.3 素数的判定

朴素的方法是让 $i$ 从 $2$ 到 $m-1$ 枚举，若 $m\ mod\ i=0$，则不是素数，退出循环。最后到循环结束的时候，便能判定为素数，这里不给出代码。

上面的方法时间复杂度是 $O(m)$ 的，如果要判断多次素数，未免太劣。

考虑一个优化：如果正整数 $m$ 有一个因数 $a>\sqrt m$，则一定有一个因数 $b<\sqrt m$。我们只用枚举到 $\sqrt m$ 就行了。

代码如下：

bool is_prime(int x)
{
    if(x==1)return 0;
    for(int i=2;i*i<=x;i++)
        if(x%i==0)return 0;
    return 1;
}

这样做时间复杂度是 $O(\sqrt m)$，能解决一部分情况。但这样还不够，之后会讲 $O(k\ log\ m)$ 的 $\textbf{Miller\_rabin}$ 算法。

3.4 素数筛

3.4.1 埃氏筛

要把 $1\sim n$ 里面的素数全都筛出来，怎么做呢？

朴素的做法是每一个数都判一遍，但这样时间复杂度就爆炸了。

考虑一个方法：如果一个数 $p$ 是素数，则 $i*p$ 肯定是合数，其中 $i$ 是大于 $1$ 的整数。

那我们先把 $1$ 至 $n$ 标记一遍，我们枚举到 $p$ 的时候，如果 $p$ 被标记，就把 $p*i(i>1,i\in Z)$ 全部取消标记。

代码如下：

void Eratosthenes(int n) 
{
    is_prime[0]=is_prime[1]=0;
    for(int i=2;i<=n;++i)is_prime[i]=true;
    for(int i=2;i<=n;++i) 
    {
        if(is_prime[i]) 
        {
            if(i*i>n)continue;
            for(int j=i*i;j<=n;j+=i)
                is_prime[j]=0;
            //注意这里i*2至i*(i-1)全都被标记过
            //所以直接从i*i开始标记
        }
    }
}

时间复杂度 $O(n\ log\ log\ n)$。

3.4.2 欧拉筛

我们发现，在埃氏筛中，每个素数可能被筛了多次。这样会提高时间复杂度。能不能使每个素数只被筛到一次？

欧拉筛的做法：我们枚举 $2\sim n$，若 $i$ 没被标记，则 $i$ 为素数，加入 $prime$数组，$cnt++$。然后，遍历 $i$ 的倍数，将 $prime[j]*i(1\leq j\leq cnt)$ 标记，若 $i\ mod\ prime[j]=0$，则退出循环。

接下来，我们证明其正确性。

首先，对于一个合数 $x$，容易证明，让 $p$ 为 $x$ 的最小质因数，我们总能分解为一个素数 $p$ 乘一个整数 $y$，其中 $p\leq y$。所以遍历到 $i$ 的时候，标记 $prime[j]*i(1\leq j\leq cnt)$，是可以遍历每一个合数的。

那为什么当 $i\ mod\ prime[j]=0$，可以退出循环呢？

假设 $i=k*prime[j]$。那我们枚举之后的 $prime[j+1],prime[j+2],\cdots$ 时，就有 $i*prime[j+q](q>0,q\in Z)=k*prime[j]*prime[j+q]$。
容易发现，在之后枚举 $k*prime[j+q]$ 的倍数时，也可以标记 $i*prime[j+q]$，就不用劳烦 $i$ 来枚举了。

这样每个数只被遍历到一遍，时间复杂度 $O(n)$。

代码如下：

void euler()
{
    pd[1]=1;
    for(int i=1;i<=n;i++)
    {
        if(pd[i]==0)prime[++cnt]=i;
        for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
        {
            pd[i*prime[j]]=1;
            if(i%prime[j]==0)break; 
        }
    }
    return;
}

3.5 威尔逊定理

内容：

对于素数 $p$，有 $1*2*\cdots\ *(p-1)\equiv -1(mod\ p)$，即 $(p-1)!\equiv -1(mod\ p)$。

证明：

你可能会认为，余数怎么可能会出现负数呢？其实，这里的 $\equiv -1$，等价于 $\equiv p-1$。

我们先特判，对于 $p=2$ 的情况，显然是成立的。

对于 $p>2$ 的情况，显然 $p-1$ 为偶数，对于每个数，明显有一个 $mod\ p$ 意义下的逆元与其对应。而且，因为 $(a^{-1})^{-1}=a$，所以我们可以把这 $p-1$ 个数分成 $\frac{p-1}{2}$ 对，每一对中的数互为逆元。

但是，还要考虑到 $a=a^{-1}$，即 $a^2=1$ 的情况。明显，解得 $a=1$ 或 $-1($即$p-1)$。把这两个数单独拿出来，剩下的数乘积 $mod\ p$ 肯定为 $1$（因为互为逆元）。最后乘上这两个数，于是能得到 $-1$，证明完毕。

3.6 费马小定理

内容：

若$p$为素数，$gcd(a,p)=1$,则 $a^p\equiv a(mod\ p)$，即 $a^{p-1}\equiv 1(mod\ p)$。

证明：

我们构造一个序列 $A=\{1,2,\cdots,p-1\}$。将 $A$ 中任一元素乘上 $a$，得到 $A=\{a,2a,\cdots,(p-1)*a\}$。

事实上，新得到的 $A$ 中任一元素对于模 $p$ 不等于 $0$，且互不同余。

前者容易证明，后者假设 $xa\equiv ya(mod\ p)$，因为 $gcd(a,p)=1$，所以能得到 $x\equiv y(mod\ p)$，显然不成立。

所以，

$1*2*\cdots *(p-1)\equiv a*2a*\cdots (p-1)*a(mod\ p)$
$1*2*\cdots *(p-1)\equiv a^{p-1}*1*2*\cdots *(p-1)(mod\ p)$
$\because gcd((p-1)!,p)=1$
$\therefore a^{p-1}\equiv 1(mod\ p)$（这就是费马小定理！）

3.7 Miller_rabin判素数法与卡迈尔数

根据费马小定理，我们知道当 $p$ 为素数且 $gcd(a,p)=1$ 时，$a^{p-1}\equiv1(mod\ p)$。这能说明，当一个数 $p$ 满足 $a^{p-1}\equiv 1(mod\ p)$时，$p$ 就是素数吗？

并不行。举个反例：$2^{340}\equiv 1(mod\ 341)$，但 $341=11*31$。我们把满足上面所述条件的数，称为卡迈尔数。同时定义卡迈尔函数为对任意满足 $$gcd(a,n)=1(n\in N_+)$$ 的整数 $$a$$，满足 $a^{m}\equiv 1(mod\ n)$ 的最小正整数 $m$。记作 $\lambda(n)$，如 $\lambda(8)=2$。

虽然靠费马小定理判素数似乎走不通，但我们还是有方法，很简单：多找几个 $a$ 试几次就行了，这样做正确概率是非常非常大的。

同时，我们还有二次探测法。

原理：若 $a^2\equiv 1(mod\ p)$，则 $a\equiv1(mod\ p)$ 或 $a\equiv p-1(mod\ p)$

所以，我们令 $k=p-1$，判断 $k$ 是否为偶数，如果是就除以 $2$，同时计算 $a^k$，然后对 $p$ 取模判断。如果是奇数或者 $mod\ p$ 为 $p-1$，直接退出。

代码如下：

ll n,test[10]={2,3,13,17,61};
ll quickpow(ll a,ll p,ll mod)
{
    ll ans=1,tmp=a;
    while(p)
    {
        if(p&1)ans=(ans*tmp)%mod;
        p>>=1;
        tmp=tmp%mod*tmp%mod;
    }
    return ans%mod;
}
bool miller_rabin(ll p,ll a)
{
    ll k=p-1;
    while(k)
    {
        ll now=quickpow(a,k,p);
        if(now!=1&&now!=p-1)return 0;
        if((k&1)==1||now==p-1)return 1;
        k>>=1;
    }
    return 1;
}
inline bool isprime(ll x)
{
    for(int i=0;i<5;i++)
    	if(x==test[i])
      	    return 1;
    bool flg=0;
    for(int i=0;i<5;i++)
        if(!miller_rabin(x,test[i]))
            flg=1;
    if(!flg)return 1;
    return 0;
}

实测，选 $2,3,13,17,61$ 这几个数，失败的可能性极小。

3.8 欧拉函数与欧拉定理

欧拉定理实际上是费马小定理的扩展，用于处理$p$不为素数时的情况。

3.8.1 欧拉函数

在讲欧拉定理前，要先讲讲欧拉函数。

欧拉函数表示小于等于 $n$ 的数中与 $n$ 互质的数的个数，记作 $\varphi(n)$。例如，$\varphi(5)=4$。

3.8.2 欧拉函数的性质

1. 若 $n$ 为素数，则 $\varphi(n)=n-1$
2. 若 $n=p^k(p$ 为素数$)$，则 $\varphi(n)=(p-1)*p^{k-1}$

证明：比 $p^k$ 小的正整数有 $p^k-1$个。
其中被$p$整除的数可表示为 $p*t(t=1,2,\cdots,p^{k-1}-1)$，共有 $p^{k-1}-1$个。
所以 $\varphi(n)=p^k-1-(p^{k-1}-1)=p^k-p^{k-1}=(p-1)*p^{k-1}=p^k(1-\frac{1}{p})$

3. 欧拉函数为积性函数。（积性函数的定义：若函数 $f(x)$ 满足 $f(1)=1$ 且对任意 $a,b(a,b\in N_+,gcd(a,b)=1)$ 有 $f(a)f(b)=f(ab)$，则称 $f(x)$ 为积性函数。）

证明：在3.2.2已证明当 $m=m_1*m_2$ 且 $gcd(m_1,m_2)=1$ 时，
$Z^*_m=m_2Z^*_{m_1}+m_1Z^*_{m_2}$。根据前文对集合的加法与乘法的定义，则有 $\lvert Z^*_m\rvert= \lvert Z^*_{m_1}\rvert \lvert Z^*_{m_2}\rvert$，即 $\varphi(m)=\varphi(m_1)\varphi(m_2)$。

4. 将 $n$ 分解质因数：$n=p_1^{a_1}*p_2^{a_2}*\cdots*p_k^{a_k}$，则有 $\varphi(n)=n*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*\cdots*(1-\frac{1}{p_k})$

证明：明显 $p_1^{a_1},\cdots,p_k^{a_k}$ 互质。所以套用性质 $2$ 和性质 $3$：
$\varphi(n)=\varphi(p_1^{a_1})\varphi(p_2^{a_2})\cdots\varphi(p_k^{a_k})=p_1^{a_1}p_2^{a_2}\cdots p_k^{a_k}(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_k})=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_k})$

3.8.3 线性筛欧拉函数

线性筛欧拉函数要用到欧拉筛。
我们可以利用欧拉筛中每个数只筛到一次的性质来计算 $\varphi(n)$。
若 $i=p^k$（$p$为质数），直接 $\varphi(i)=p^{k-1}(p-1)$ 就行了；
若 $i\ mod\ p=0$，则 $\varphi(i*p)=p*\varphi(i)$；
若 $i\ mod\ p\neq0$，则 $\varphi(i*p)=(p-1)*\varphi(i)$；

代码如下：

void fndeuler()
{
    pd[1]=1,euler[1]=0;
    for(int i=1;i<=n;i++)
    {
        if(pd[i]==0)prime[++cnt]=i,euler[i]=i-1;
        for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
        {
            pd[i*prime[j]]=1;
            if(i%prime[j]==0)
            {
                euler[i*prime[j]]*=prime[j];
                break; 
            }
            else euler[i*prime[j]]*=prime[j]-1;
        }
    }
    return;
}

3.8.4 欧拉定理

内容：

若 $gcd(a,m)=1$，则 $a^{\varphi(m)}\equiv 1(mod\ m)$。

证明：

我们构造一个序列$A=\{p_1,\cdots,p_{\varphi(m)}\}(gcd(p_i,m)=1)$。将$A$中任一元素乘上$a$，得到$A=\{p_1a,\cdots,p_{\varphi(m)}*a\}$。之后的证明与费马小定理类似，这里省略。

3.9 扩展欧拉定理

欧拉定理只适用于 $gcd(a,m)=1$ 时的情况。而扩展欧拉定理则不用到这个条件，是欧拉定理的扩展。

内容：

当 $a,m\in \mathbb{Z}$ 时，有

\[ a^b\equiv\left\{ \begin{aligned} a^b,&&gcd(a,m)\neq1,b<\varphi(m), \\ a^{b\ mod\ \varphi(m)},&&gcd(a,m)=1,& &(mod\ m)\\ a^{((b\ mod\ \varphi(m)+\varphi(m))},&&gcd(a,m)\neq1,b\geq\varphi(m) \end{aligned} \right. \]

证明：

第一式显然；

第二式可以用前文的欧拉定理来证明。设 $b\ mod\ \varphi(m)=r$（即设$b=k*\varphi(m)+r$），则 $a^b=a^{\varphi(m)^k}*a^r=1^k*a^r=a^r$;

重点在于第三式的证明。

我们使 $a$ 质因数分解：$a=p_1^{k_1}p_2^{k_2}\cdots p_n^{k_n}$。根据同余的性质，只要能证明 $a^b\equiv a^{((b\ mod\ \varphi(m)+\varphi(m))}(mod\ p_i^{k_i})$，就可以证明上式。这里我们分情况讨论。

1. 当 $gcd(a,p_i^{k_i})=1$时，与第二式证明类似，设 $b\ mod\ \varphi(m)=r$（即设 $b=k*\varphi(m)+r$），则$a^b=a^{\varphi(m)^k}*a^r$。

因为欧拉函数为积性函数，所以 $\varphi(m)$ 是 $\varphi(p_i^{k_i})$ 的倍数（因为 $m$ 是 $p_i^{k_i}$ 的倍数）。

所以 $a^{\varphi(m)}\equiv 1(mod\ p_i^{k_i})$，即 $a^b\equiv\ a^r(mod\ p_i^{k_i})$，就可以得到 $a^b\equiv a^{b\ mod\ \varphi(m)}(mod\ p_i^{k_i})$。

2. 当 $gcd(a,p_i^{k_i})\neq1$ 时，有 $\varphi(p_i^{k_i})\geq k_i$。
（下面给出证明：
根据欧拉函数的性质，有 $\varphi(p_i^{k_i})=p_i^{k_i-1}(p_i-1)=p_i^{k_i}-p_i^{k_i-1}$.
我们证明 $p_i^{k_i}-p_i^{k_i-1}-k_i\geq 0$ 就行了。
虽然我不会证，但可以上图！

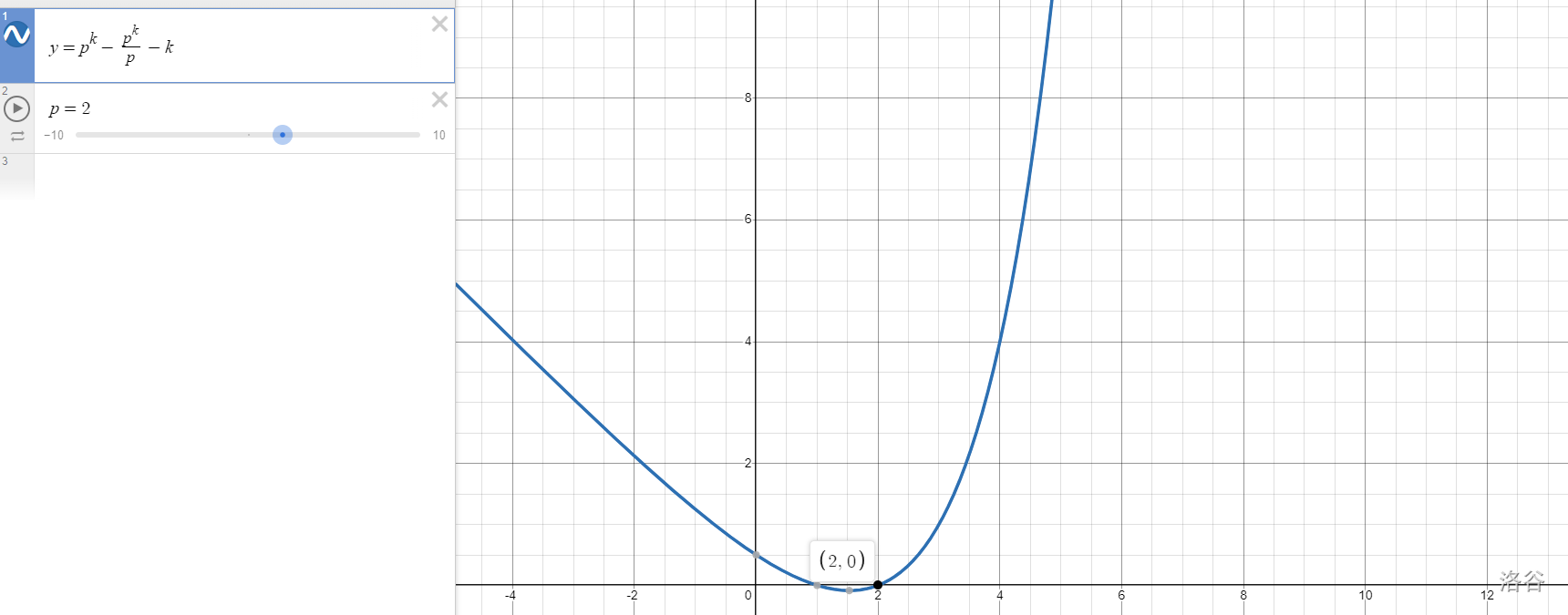
（如果看不清可以点这里）
注意到 $p=2,k>1$ 且 $k$ 为整数时，当且仅当 $k=1$ 或 $2$ 时 $p_i^{k_i}-p_i^{k_i-1}-k_i=0$.
$p=3$ 也放一张图：
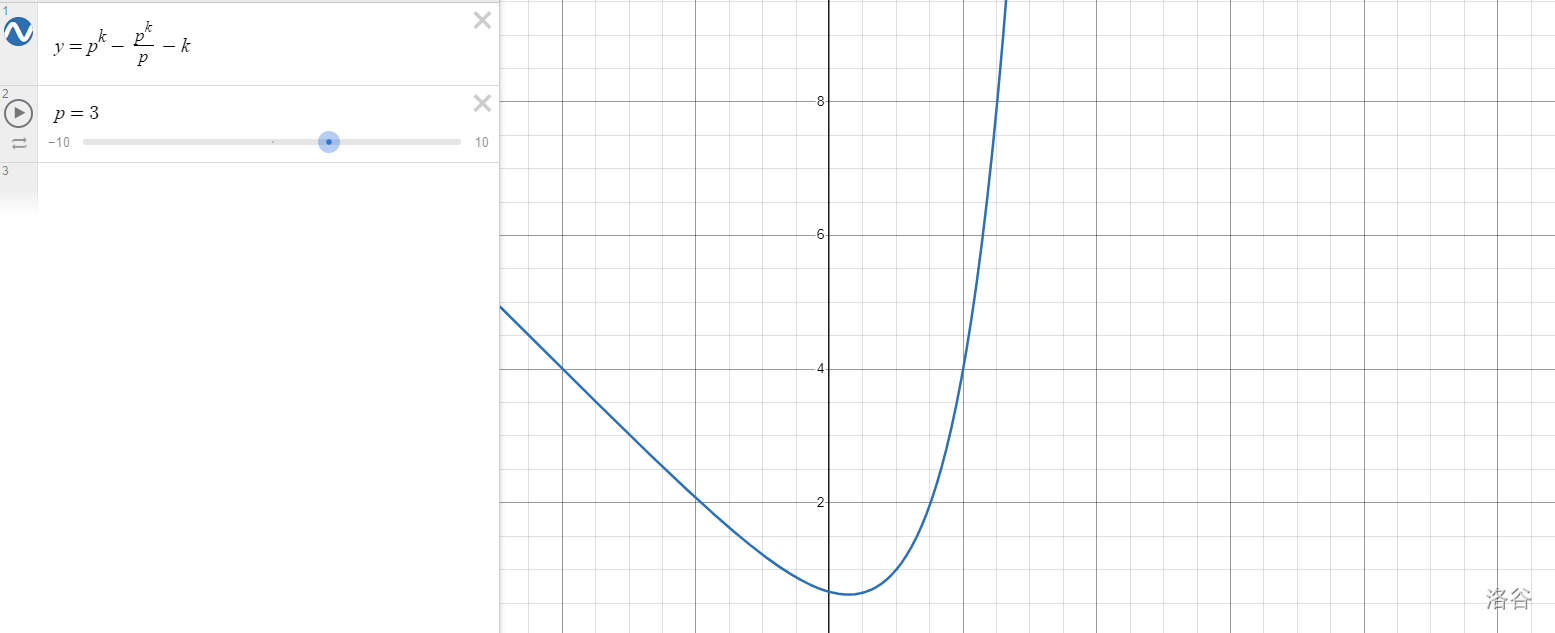（如果看不清可以点这里）
容易证明 $p>2$ 时，不等式是显然成立的，于是就证完了。实在不懂的可以去desmos上手动画图）
所以，有 $b\geq\varphi(m)\geq\varphi(p_i^{k_i})\geq k_i$.
$a^b$ 就是 $p_i^{k_i}$ 的倍数，当然 $a^{\varphi(m)}$ 也是。
则有 $a^b\equiv a^{((b\ mod\ \varphi(m)+\varphi(m))}\equiv 0(mod\ p_i^{k_i})$.

于是我们就证完辣！！！

模板代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll a,m,mod,b;
bool flg;
ll phi(ll x)
{
    ll ret=1,num=1;
    for(ll i=2;i*i<=x;i++)
    {
        if(x%i==0)
        {
            num=i-1,x/=i;
            while(x%i==0)num*=i,x/=i;
            ret*=num;
        }
    }
    if(x!=1)ret*=(x-1);
    return ret;
}
ll quickpow(ll a,ll b,ll m)
{
    ll ret=1,tmp=a;
    while(b)
    {
        if(b%2==1)ret=ret*tmp%m;
        tmp=tmp*tmp%m;
        b>>=1;
    }
    return ret%m;
}
int main()
{
    cin>>a>>mod;
    m=phi(mod);
    char c=getchar();
    while(c<'0'||c>'9')c=getchar();
    while(c>='0'&&c<='9')
    {
        b=b*10+c-'0';
        if(b>=mod)flg=1,b%=m;
        c=getchar();    
    } 
    if(flg)b+=m;
    cout<<quickpow(a,b,mod);
    return 0;
}

Chapter #4 素数（二）

上一章太长了，在这里再开一个chapter $qaq$

4.1 反素数

定义：如果某个正整数 $n$ 满足如下条件，则称为是反素数：任何小于 $n$ 的正数的约数个数都小于 $n$ 的约数个数。如 $840$ 就是一个反素数。

怎样求小于等于 $n$ 的最大的反素数呢？

根据算术基本定理，我们知道如果一个数 $n$ 分解出以下形式：$n=p_1^{q_1}p_2^{q_2}\cdots p_k^{q_k}$，则 $n$ 的因数个数等于 $(q_1+1)(q_2+1)\cdots(q_k+1)$。

事实上，一个反素数的质因子必须是连续的素数。这很好证，如果不是连续的，我们绝对能找一个更小的素数替换掉，使其质因子连续而因数个数不变。在找 $int$ 范围内的反素数时，只要枚举前 $10$ 小的素数就行的，因为 $2*3*5*7*\cdots*31$（第 $11$ 个素数）$>2*10^9$ 。这时，我们用 $dfs$ 搜一遍就能找到答案。

P1463题意就是求 $n$ 以内最大反素数。

代码如下：

#include<bits/stdc++.h>
#define ll long long
ll n,ans=1e18,mx;
using namespace std;
ll pri[20]={2,3,5,7,11,13,17,19,23,29,31,33,37,41,43,47,53,57,59,61};
void dfs(ll num,ll cnt,ll prinum,ll pricnt)
{
    if(num>n||prinum>=10)return;
    if(cnt*(pricnt+1)>=mx)
    {
        if(cnt*(pricnt+1)>mx)ans=num;
        else ans=min(ans,num);
        mx=cnt*(pricnt+1);
    }
    dfs(num,cnt*(pricnt+1),prinum+1,0);//选下一个素数
    dfs(num*pri[prinum],cnt,prinum,pricnt+1);//选这个素数 
    return;
}
int main()
{
    cin>>n;
    dfs(1,1,0,0);
    cout<<ans;
    return 0;
}

4.2 Pollard Rho 算法

对于一个数 $n$ ，我们怎么快速找到它的一个因数（除了 $1$ 和 $n$）呢？

朴素的思想是从 $2$ 到 $\sqrt{n}$ 枚举，但当 $n$ 到了 $10^{18}$ 这个数量级的时候，枚举就像大海捞针一样不管用了，我们要找到一个更快的算法。

这时就需要Pollard Rho 算法的登场了。

问题：一个房间里至少要多少人，才能使其中两人生日相同的概率达到 $50\%$ ？（假设一年 $365$ 天）

事实上，这个问题的答案是 $23$ 人！听上去很不可思议。

让我们想想，两个人生日互不相同的概率是多少？答案很简单，为 $\frac{364}{365}$。三个人呢？根据概率论相关知识，得出答案是 $\frac{364}{365}*\frac{363}{365}$ 。于是可以推出，$k$ 个人生日互不相同的概率为 $\frac{1}{365^{k-1}}*\frac{364!}{(365-k)!}$。则 $k$ 个人中有两人生日相同的概率 $P$ 为 $1-\frac{1}{365^{k-1}}*\frac{364!}{(365-k)!}$ 。当 $k=23$ 时，可算出 $P\approx 0.507$。

进一步计算得出，当一年有 $n$ 天时，当房间有约 $\sqrt{2n \ln 2}$ 个人时，使其中两人生日相同的概率约为 $50\%$ 。

Pollard Rho 算法的基本原理：若存在一个正整数 $q$ 使得 $gcd(q,n)>1$ ，则有 $gcd(q,n)$ 为 $n$ 的一个因数。

我们可以随机取两个数 $x_1$ 和 $c$ ，然后使 $x_{i+1}=f(x_i)=({x_i}^2+c)\ mod\ n$。这样可以生成一个序列 $\{x_1,x_2,...,x_n\}$。这样就可以取 $x_i-x_{i-1}$ 取最大公因数了。计算得出这种方法找质因数时间复杂度 $\sqrt{\sqrt{n}}$。

但是这样取有个问题：这样取，到后面就可能有循环的地方。举个例子：$n=13,c=5,x_1=7$时，序列是这样的：$$7,12,6,2,9,8,0,5,12,...$$

我们发现，它出现了循环！必须要处理掉！

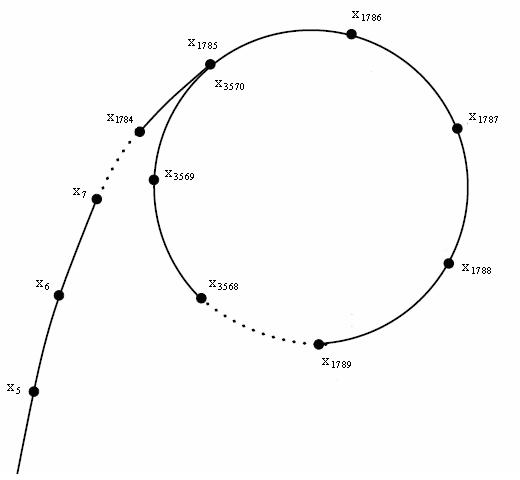
（这里的循环类似于这样，像一个rho形，所以叫pollard rho 算法）

有一个奇妙又有趣的方法：假设 $m=f(x_1),n=f(f(x_1))$，且 $m=f(m),n=f(f(n))$，那么 $n$ 比 $m$ 快 $1$ 倍，如果是在环上，那 $n$ 一定会在一个地方追上 $m$。当追上的时候，就可以退出了。这就是 $\rm{floyd}$ 判环大法。

但是这样搞取的 $gcd$ 可能过多，时间复杂度直接爆炸。于是又有一个倍增优化法：如果 $gcd(a,x)>0$，则有 $gcd(ac,x)>0$。于是我们把每次作差的结果乘起来，每隔 $2^k-1$ 次取一遍 $gcd$，效率更高，这里取常用的 $k=7$。

结合 $Miller\ rabin$ 判素数法，可以得到分解质因数的全过程：首先判 $n$ 是否为素数，若不是就放到 $pollard\ rho$ 函数分解出一个质因数。将这个过程不断循环，直到不能分解为止。

模板代码如下：

#include<bits/stdc++.h>
#define ll long long
#define Il inline
#define lit __int128
#define maxn 100010
using namespace std;
int T;
ll n,ans,test[5]={2,3,61,17,13};
Il ll gcd(ll a,ll b)
{
    if(b==0)return a;
    return gcd(b,a%b);
}
Il ll quickpow(ll a,ll p,ll mod)
{
    ll ans=1,tmp=a;
    while(p)
    {
        if(p&1)ans=((lit)ans*tmp)%mod;//__int128更快且保险 
        p>>=1;
        tmp=(lit)tmp%mod*tmp%mod;
    }
    return ans%mod;
}
bool miller_rabin(ll p,ll a)
{
    
    ll k=p-1;
    while(k)
    {
        ll now=quickpow(a,k,p);
        if(now!=1&&now!=p-1)return 0;
        if((k&1)==1||now==p-1)return 1;
        k>>=1;
    }
    return 1;
}
inline bool isprime(ll x)
{
    for(int i=0;i<5;i++)
        if(x==test[i])
            return 1;
    bool flg=0;
    for(int i=0;i<5;i++)
        if(!miller_rabin(x,test[i]))
            flg=1;
    if(!flg)return 1;
    return 0;
}
Il ll pollardrho(ll x)
{
    ll a=0,b=0,c=1ll*rand()%(x-1)+1/*防止c为0*/;
    ll len=1,i,num,v;
    while(1)
    {
        a=b,num=1;
        for(i=1;i<=len;i++)
        {
            b=((lit)b*b+c)%x;
            num=(lit)num*abs(a-b)%x;
            if(i%127==0)
            {
                v=gcd(x,num);
                if(v>1)return v;
            }
        }
        v=gcd(num,x);
        if(v>1)return v;
        len<<=1;
    }
}
Il void fac(ll x)
{
    if(x<=ans||x<2)return;
    if(isprime(x))
    {
        ans=max(ans,x);
        return;
    }
    ll x1=x;
    while(x1>=x)
        x1=pollardrho(x);
    while(x%x1==0)x/=x1;
    fac(x);
    fac(x1);
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>T;
    while(T--)
    {
        srand(time(0));
        cin>>n;
        ans=0;
        fac(n);
        
    }    
	return 0;
}

4.3 卢卡斯定理

前置知识：组合数指 $n$ 个不同元素里不考虑顺序选 $m$ 个元素组成的集合数，记作 $C_n^m$，即$\tbinom{n}{m}$ 。公式为：

\[\tbinom{n}{m}=\frac{n!}{m!(n-m)!} \]

详细解释见此

内容：$$\Large{\tbinom{n}{m}}$$ $$mod\ p=$$ $$\Large{\tbinom{\lfloor n/p\rfloor}{\lfloor m/p\rfloor}}$$ $$*$$ $$\Large{\tbinom{n\ mod\ p}{m\ mod\ p}}$$ $$mod\ p$$ ($p$ 为素数)

证明：
首先要证明一个东西：
$\tbinom{p}{i}$ $=\frac{p!}{i!(p-i)!}=\frac{p}{i}\frac{(p-1)!}{(i-1)!(p-i)!}=\frac{p}{i}$ $\tbinom{p-1}{i-1}$ $(1\leq i<p)$

于是
$\tbinom{p}{i}$ $\equiv\frac{p}{i}$ $\tbinom{p-1}{i-1}$ $\equiv 0\ (mod\ p)$

我们先随便拉一个 $x$ 过来，根据二项式定理有
$(1+x)^p=\tbinom{p}{0}+\tbinom{p}{1}x^1+...+\tbinom{p}{p}x^p\equiv1+x^p(mod\ p)$

令 $a=\lfloor n/p\rfloor,b=\lfloor m/p\rfloor,c=n\ mod\ p,d=m\ mod\ p$，即 $n=ap+c,m=bp+d$
有 $(1+x)^n=(1+x)^{ap}(1+x)^c=((1+x)^p)^a(1+x)^c\equiv(1+x^p)^a(1+x)^c(mod\ p)$
即 $(1+x)^n\equiv (1+x^p)^a(1+x)^c(mod\ p)$

关键在这里！我看了很多解释都是一句话带过了！
这里我们要单独把带 $x^m$ 的项抽出来。

左边：$(1+x)^n=\tbinom{n}{0}x^0+\tbinom{n}{1}x^1+...+\tbinom{n}{n}x^n$，其中带 $x^m$ 的项为 $\tbinom{n}{m}x^m$

右边：看上去有些乱哈。不过我们还是可以选出来。注意到 $m=bp+d$，可以从 $(1+x^p)^a$ 中选 $\tbinom{a}{b}x^{bp}$，从 $(1+x)^c$中选 $\tbinom{c}{d}x^d$。组合到一起有 $\tbinom{a}{b}x^{bp}\tbinom{c}{d}x^d$

于是，有 $\tbinom{n}{m}x^m\equiv \tbinom{a}{b}x^{bp}\tbinom{c}{d}x^d\ (mod\ p)$
即$\tbinom{n}{m}x^m\equiv \tbinom{a}{b}\tbinom{c}{d}x^m\ (mod\ p)$
显然可以有 $gcd(x^m,p)=1$（毕竟 $x$ 是随便找的，且 $p$ 为素数）
所以 $\tbinom{n}{m}\equiv \tbinom{a}{b}\tbinom{c}{d}\ (mod\ p)$

替换回去，有 $\tbinom{n}{m}\equiv$ $\tbinom{\lfloor n/p\rfloor}{\lfloor m/p\rfloor}$ $*$ $\tbinom{n\ mod\ p}{m\ mod\ p}$ $(mod\ p)$
这不就是卢卡斯定理吗？

模板代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll T,n,m,p;
ll quickpow(ll a,ll x,ll p){
    ll ret=1,base=a;
    while(x){
        if(x&1==1)ret=ret*base%p;
        base=base*base%p;
        x>>=1;
    }
    return ret;
}
ll C(ll n,ll m,ll p){
    if(m<0||m>n)return 0;
    ll ret=1,div=1;
    for(int i=0;i<m;i++) 
        ret=(ret*(n-i))%p,div=(div*(i+1))%p;
    return ret*quickpow(div,p-2,p)%p;//利用了快速幂法求(n-m)!mod p的逆元
}
ll lucas(ll n,ll m){
    if(!m)return 1;
    return lucas(n/p,m/p)*C(n%p,m%p,p)%p;
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>T;
    while(T--){
        cin>>n>>m>>p;
        cout<<lucas(n+m,m)<<'\n';
    }
	return 0;
}

4.4 扩展卢卡斯定理

前置知识：扩展中国剩余定理（当然如果你一路看下来肯定就会了）

好吧，卢卡斯定理还是太局限了，如果模数不是素数，那这定理又没啥用了。于是，我们必须找一个全新的方法。

问题：求 $\tbinom{n}{m}\ mod\ p$

我们知道 $\tbinom{n}{m}=\frac{n!}{m!(n-m)!}$
首先，设 $p=p_1^{a_1}p_2^{a_2}...p_k^{a_k}$
求出
$ \left\{ \begin{aligned} \tbinom{n}{m}\ mod p_1^{a_1}\\ \tbinom{n}{m}\ mod p_2^{a_2}\\ ...\\ \tbinom{n}{m}\ mod p_k^{a_k} \end{aligned} \right. $
最后用中国剩余定理合并答案就行了。
我们求不出 $m!$ 和 $(n-m)!\ mod\ p_i^{a_i}$ 的逆元，因为很可能解不出来。
所以我们如果能把 $n!$ 中 $p$ 因子的个数求出来，记作 $p^x$。
对于 $m!$ 和 $(n-m)!$ 我们也这么搞，记作 $p^y$ 和 $p^z$。
然后算出 $\LARGE\frac{\frac{n!}{p^x}}{\frac{n!(n-m)!}{p^yp^z}}$ $p^{x-y-z}\ mod\ p^a$ 就行了。

问题现在转化成：对于一个数 $n$，求出 $\frac{n!}{p^a}$，其中 $a$ 为 $n!$ 中包含 $p$ 因子的个数。

SP1：快速幂

虽然快速幂并非数论的内容，但它在许多内容里出现过，所以这里必须要讲讲。

SP1.1 解释

怎样求一个数的 $n$ 次方呢？朴素的想法是一个一个乘。但是，当 $n$ 特别大的时候，直接乘显然会 $TLE$。因此，才有了快速幂。

快速幂的基本思想是将幂按二进制划分。举个例子：

$3$ 的 $114$ 次方怎么求呢？

我们知道，

$114=(1110010)_2=2^6+2^5+2^4+2^1$

我们还知道，

$a^{b+c}=a^b*a^c$

所以，

$3^{114}=3^{2^6}*3^{2^5}*3^{2^4}*3^{2^1}$

我们可以计算出 $3$ 的 $2^k$ 次方，然后在用二进制分解 $n$ 的时候乘起来就可以了。

快速幂可类比于此。

模板代码如下：

#define ll long long
ll quickpow(ll a,ll b,ll p)
{
    ll answer=1,tmp=a;
    while(b!=0)
    {
        if(b%2==1)
            answer=answer%p*tmp%p;
        tmp=tmp%p*tmp%p;
        b/=2;//由于c++除法向下取整，所以可以直接除
    }
    answer%=p;
    return answer;
}