Sternhalma

我们给格子编个号,然后暴力打表出一个格子可以走到哪些点,然后状压 \(dp\),从全 \(1\) 的情况开始倒推,每次查询将其转化为二进制数列即可

#include <bits/stdc++.h>

using namespace std;

using pii = pair<int, int>;

const int N = 21, M = (1 << 19);

int q, n, a[N][N], len[] = {0, 3, 4, 5, 4, 3}, dp[N][M];

vector<int> road1[N];

vector<int> road2[N];

char x[N][N];

vector<int> v[21];

bool check(int x, int y) {
  if (x < 1 || x > 5 || y < 1 || y > len[x]) {
    return false;
  }
  return true;
}

int change(int x, int y) {
  int ans = 0;
  for (int i = 1; i < x; i++) {
    ans += len[i];
  }
  return ans + y;
}

pii one_to_two(int x) {
  for (int i = 1; i <= 5; i++) {
    if (x <= len[i]) {
      return {i, x};
    }
    x -= len[i];
  }
}

void Solve() {
  int cnt = 0, res = 0;
  for (int i = 1; i <= 5; i++) {
    for (int j = 1; j <= len[i]; j++) {
      cin >> x[i][j];
      cnt += (x[i][j] == '#');
      res += (1 << (change(i, j) - 1)) * (x[i][j] == '#');
    }
  }
  cout << dp[cnt][res] << "\n";
}

int main() {
  ios::sync_with_stdio(0);
  cin.tie(0);
  for (int i = 0; i <= (1 << 19) - 1; i++) {
    int p = i, cnt = 0;
    while (p) {
      cnt += (p & 1);
      p >>= 1;
    }
    v[cnt].push_back(i);
  }
  road1[1].push_back(2), road1[1].push_back(4), road1[1].push_back(5);
  road2[1].push_back(3), road2[1].push_back(8), road2[1].push_back(10);
  road1[2].push_back(5), road1[2].push_back(6);
  road2[2].push_back(9), road2[2].push_back(11);
  roa d1[3].push_back(2), road1[3].push_back(6), road1[3].push_back(7);
  road2[3].push_back(1), road2[3].push_back(10), road2[3].push_back(12);
  road1[4].push_back(5), road1[4].push_back(9);
  road2[4].push_back(6), road2[4].push_back(14);
  road1[5].push_back(6), road1[5].push_back(10), road1[5].push_back(9);
  road2[5].push_back(7), road2[5].push_back(15), road2[5].push_back(13);
  road1[6].push_back(5), road1[6].push_back(10), road1[6].push_back(11);
  road2[6].push_back(4), road2[6].push_back(14), road2[6].push_back(16);
  road1[7].push_back(6), road1[7].push_back(11);
  road2[7].push_back(5), road2[7].push_back(15);
  road1[8].push_back(4), road1[8].push_back(9), road1[8].push_back(13);
  road2[8].push_back(1), road2[8].push_back(10), road2[8].push_back(17);
  road1[9].push_back(5), road1[9].push_back(10), road1[9].push_back(14);
  road2[9].push_back(2), road2[9].push_back(11), road2[9].push_back(18);
  road1[10].push_back(5), road1[10].push_back(6), road1[10].push_back(11);
  road2[10].push_back(1), road2[10].push_back(3), road2[10].push_back(12);
  road1[10].push_back(15), road1[10].push_back(14), road1[10].push_back(9);
  road2[10].push_back(19), road2[10].push_back(17), road2[10].push_back(8);
  road1[11].push_back(6), road1[11].push_back(10), road1[11].push_back(15);
  road2[11].push_back(2), road2[11].push_back(9), road2[11].push_back(18);
  road1[12].push_back(7), road1[12].push_back(11), road1[12].push_back(16);
  road2[12].push_back(3), road2[12].push_back(10), road2[12].push_back(19);
  road1[13].push_back(9), road1[13].push_back(14);
  road2[13].push_back(5), road2[13].push_back(15);
  road1[14].push_back(9), road1[14].push_back(10), road1[14].push_back(15);
  road2[14].push_back(4), road2[14].push_back(6), road2[14].push_back(16);
  road1[15].push_back(11), road1[15].push_back(10), road1[15].push_back(14);
  road2[15].push_back(7), road2[15].push_back(5), road2[15].push_back(13);
  road1[16].push_back(11), road1[16].push_back(15);
  road2[16].push_back(6), road2[16].push_back(14);
  road1[17].push_back(13), road1[17].push_back(14), road1[17].push_back(18);
  road2[17].push_back(8), road2[17].push_back(10), road2[17].push_back(19);
  road1[18].push_back(14), road1[18].push_back(15);
  road2[18].push_back(9), road2[18].push_back(11);
  road1[19].push_back(16), road1[19].push_back(15), road1[19].push_back(18);
  road2[19].push_back(12), road2[19].push_back(10), road2[19].push_back(17);
  for (int i = 1; i <= 5; i++) {
    for (int j = 1; j <= len[i]; j++) {
      cin >> a[i][j];
    }
  }
  memset(dp, 0xcf, sizeof(dp));
  dp[0][0] = 0;
  for (int i = 0; i < 19; i++) {
    for (auto j : v[i]) {
      for (int x = 1; x <= 19; x++) {
        if ((j & (1 << (x - 1)))) {
          continue;
        }
        dp[i + 1][j + (1 << (x - 1))] = max(dp[i + 1][j + (1 << (x - 1))], dp[i][j]);
        for (int l = 0; l < road1[x].size(); l++) {
          int tot1 = (1 << (road1[x][l] - 1));
          int tot2 = (1 << (road2[x][l] - 1));
          if (!(j & tot1) && (j & tot2)) {
            dp[i + 1][(j + tot1 + (1 << (x - 1))) - tot2] = max(dp[i + 1][(j + tot1 + (1 << (x - 1))) - tot2], dp[i][j] + a[one_to_two(road1[x][l]).first][one_to_two(road1[x][l]).second]);
          }
        }
      }
    }
  }
  cin >> q;
  while (q--) {
    Solve();
  }
  return 0;
}

Honeycomb

我们可以将每一个格子进行染色,至于如何染色我们可以找到如下这个字符

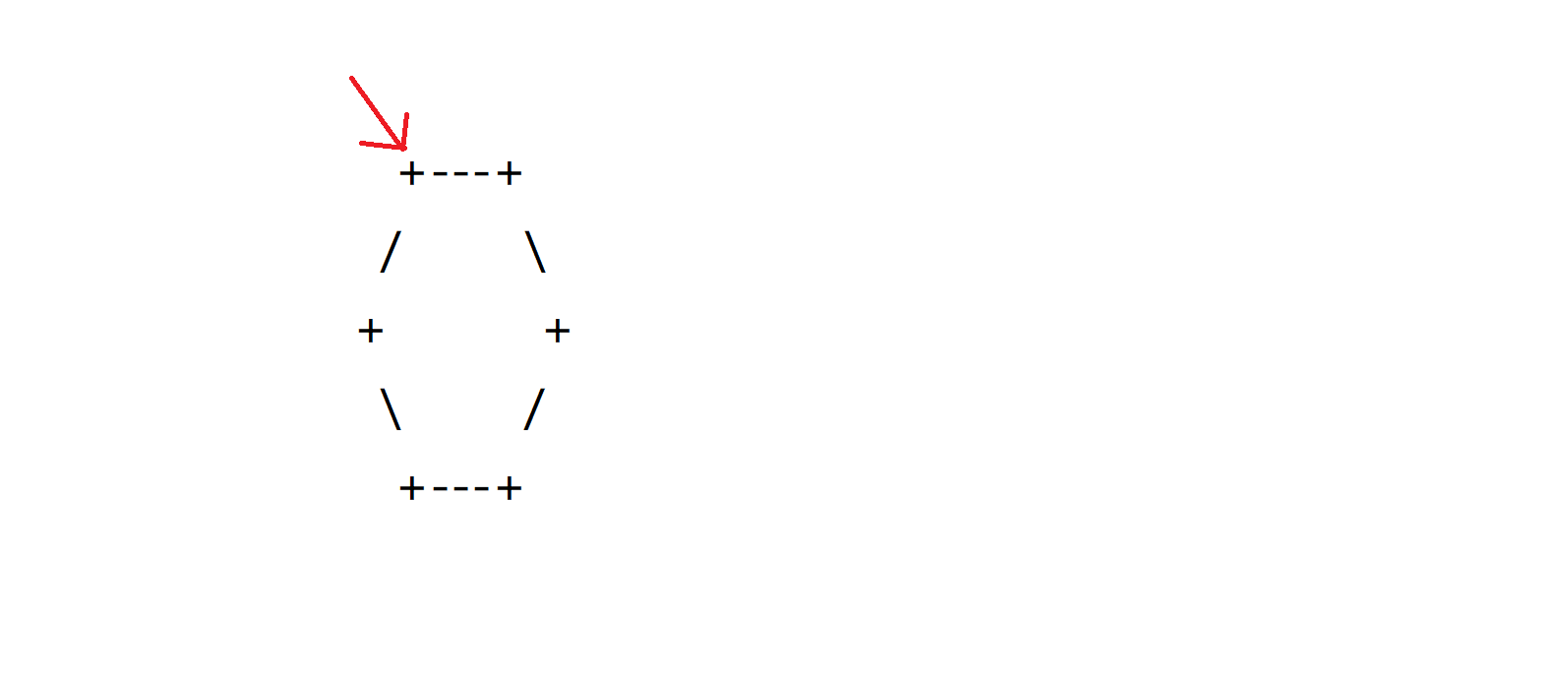
然后打表即可,假设我们只能自己走空格,那我们就可以用 \(bfs\) 答案就是经过了几个不同颜色的空格

#include <bits/stdc++.h>

using namespace std;

const int N = 6e3 + 5;

struct node {
  int x, y, dis;
};

int t, n, m, len[N], cnt, qx, qy, zx, zy;

int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};

bool vis[N][N];

char a[N][N];

int b[N][N];

string s;

void bfs() {
  deque<node> q;
  q.push_front({qx, qy, 1});
  while (!q.empty()) {
    node cur = q.front();
    q.pop_front();
    vis[cur.x][cur.y] = true;
    if (cur.x == zx && cur.y == zy) {
      cout << cur.dis << "\n";
      return ;
    }
    for (int i = 0; i < 4; i++) {
      int nx = cur.x + dx[i], ny = cur.y + dy[i];
      if (nx >= 1 && nx <= 3 + 4 * n && ny >= 1 && ny <= len[nx] && (a[nx][ny] == ' ' || a[nx][ny] == 'T') && !vis[nx][ny]) {
        if (b[nx][ny] != b[cur.x][cur.y]) {
          q.push_back({nx, ny, cur.dis + 1});
        }
        else q.push_front({nx, ny, cur.dis});
      }
    }
  }
  cout << "-1\n";
}

void Solve() {
  cin >> n >> m;
  getline(cin, s);
  for (int i = 1; i <= 3 + n * 4; i++) {
    getline(cin, s);
    len[i] = s.size();
    for (int j = 0; j < s.size(); j++) {
      a[i][j + 1] = s[j];
      if (a[i][j + 1] == 'S') {
        qx = i, qy = j + 1;
      }
      else if (a[i][j + 1] == 'T') {
        zx = i, zy = j + 1;
      }
    }
  }
  cnt = 0;
  for (int i = 1; i <= n * 4; i++) {
    int tot = (i % 4) / 2;
    for (int j = 1; j <= len[i]; j++) {
      if (a[i][j] != '+') {
        continue;
      }
      tot++;
      if (!(tot % 2) || j == len[i]) {
        continue;
      }
      cnt++;
      b[i][j + 1] = b[i][j + 2] = b[i][j + 3] = cnt;
      b[i + 1][j - 1] = b[i + 1][j] = b[i + 1][j + 1] = b[i + 1][j + 2] = b[i + 1][j + 3] = b[i + 1][j + 4] = b[i + 1][j + 5] = cnt;
      b[i + 2][j - 2] = b[i + 2][j - 1] = b[i + 2][j] = b[i + 2][j + 1] = b[i + 2][j + 2] = b[i + 2][j + 3] = b[i + 2][j + 4] = b[i + 2][j + 5] = b[i + 2][j + 6] = cnt;
      b[i + 3][j - 1] = b[i + 3][j] = b[i + 3][j + 1] = b[i + 3][j + 2] = b[i + 3][j + 3] = b[i + 3][j + 4] = b[i + 3][j + 5] = cnt;
      b[i + 4][j + 1] = b[i + 4][j + 2] = b[i + 4][j + 3] = cnt;
    }
  }
  bfs();
  for (int i = 1; i <= 3 + 4 * n; i++) {
    for (int j = 1; j <= len[i]; j++) {
      vis[i][j] = false;
      b[i][j] = 0;
      a[i][j] = ' ';
    }
  }
}

int main() {
  ios::sync_with_stdio(0);
  cin.tie(0);
  for (int i = 1; i < N; i++) {
    for (int j = 1; j < N; j++) {
      a[i][j] = ' ';
    }
  }
  cin >> t;
  while (t--) {
    Solve();
  }
  return 0;
}

Cook and Porridge

我们可以维护两个小根堆,\(q1\) 表示等待喝粥的和 \(q2\)正在喝粥的,由于他最开始的顺序是固定的,假设当前 \(j...n\) 还没有喝粥,那么只有 \(k[j] > q1.top\) 或者 \(q1.empty()\), \(j\)才能喝上粥,也就是 \(j++\),然后我们把 \(j\) 丢进 \(q2\) 里即可,至于 \(q2\) 的处理,就是如果 \(q2.top() < i\) (\(i\) 表示当前为第几秒)就把 \(j\) 丢进 \(q1\) 中等待处理

排序规则

\(q1\) : 按照 \(k\) 的大小和进队的时间进行双关键字排序即可
\(q2\) : 按照出队时间,即 \(: x + s[i]\) 和 \(s[i]\) 进行双关键字排序即可

#include <bits/stdc++.h>

using namespace std;

const int N = 4e5 + 5;

int t, n, d, k[N], s[N], maxi[N], tim;

struct node {
  int t, id;
  bool operator < (const node &y) const {
    if (k[id] != k[y.id]) {
      return k[id] < k[y.id];
    }
    return t > y.t;
  }
};

struct F {
  int t, id;
  bool operator < (const F &y) const {
    if (t != y.t) {
      return t > y.t;
    }
    return s[id] > s[y.id];
  }
};

void Solve() {
  cin >> n >> d;
  for (int i = 1; i <= n; i++) {
    cin >> k[i] >> s[i];
  }
  maxi[n + 1] = 0;
  for (int i = n; i >= 1; i--) {
    maxi[i] = max(maxi[i + 1], k[i]);
  }
  priority_queue<node> q1;//等待喝粥
  priority_queue<F> q2;//正在喝粥
  int tot = 1;
  for (int i = 1; i <= d; i++) {
    if (tot == n + 1) {
      cout << i - 1 << "\n";
      return ;
    }
    if (q1.empty() || k[q1.top().id] <= maxi[tot]) {
      q2.push({i + s[tot], tot});
      tot++;
    }
    else {
      int cur = q1.top().id;
      q1.pop();
      q2.push({i + s[cur], cur});
    }
    while (!q2.empty() && q2.top().t == i) {
      q1.push({++tim, q2.top().id});
      q2.pop();
    }
  }
  if (tot == n + 1) {
    cout << d << "\n";
    return ;
  }
  cout << "-1\n";
}

int main() {
  ios::sync_with_stdio(0);
  cin.tie(0);
  cin >> t;
  while (t--) {
    Solve();
  }
  return 0;
}