正方形计数题解

XuYueming / 2024-09-22 / 原文

题意简述

给出一个 $n \times n$ 的格点平面，有 $q$ 次询问，求有多少正方形以 $(x, y)$ 为某一顶点，满足这个正方形顶点均在格点上，且边长为有理数。

$l \leq 10^5$，$q \leq 5 \times 10^5$。

题目分析

看到边长为有理数，想到「毕达哥拉斯三元组」（"Pythagorean triple"，简称「三元组」）。在 $n$ 范围内，这样的三元组是不多的，根据下文的生成方法可以证明组数是 $\Theta(n \log n)$ 的。我们先来讨论如何生成出这些「三元组」。

本文中只介绍最简单的「欧几里得公式」（"Euclid's formula"）来生成所有 $n$ 范围内的「三元组」。如果读者有兴趣，可以尝试阅读 Formulas for generating Pythagorean triples，并使用其他方法来解决此问题。

设生成的「三元组」为 $(a, b, c)$，那么我们根据参数 $\varphi, \lambda, k$，其中 $\varphi \gt \lambda \gt 0, \lambda \perp \varphi , k \in\mathbb{Z}_+ $ 且 $\lambda$ 和 $\varphi $ 中恰有一个偶数，根据下述公式即可生成所有「三元组」：

${\displaystyle a=k\cdot (\varphi ^{2}-\lambda^{2}),\ \,b=k\cdot (2\varphi \lambda),\ \,c=k\cdot (\varphi ^{2}+\lambda^{2})}$ ^[1]

当 $k = 1$ 时生成出来的 $(a, b, c)$ 为「本原三元组」（"primitive triple"），如 ${\displaystyle \varphi =2,\ \,\lambda=1,\, k = 1}$ 生成出 $(3, 4, 5)$。所有「三元组」都能唯一地被某一「本原三元组」和缩放系数 $k$ 生成。

使用初等代数展开，就能证明生成的算法的充分性，这部分不在赘述。考虑证明其必要性，即所有「本原三元组」都能用这样的方式表示出来。

证明 ^[1:1]：

「本原三元组」$(a, b, c)$ 满足 $a^2 + b^2 = c^2$，且 $\gcd(a, b, c) = 1$。那么有 $a$、$b$、$c$ 两两互质，那么 $a$ 和 $b$ 间至少一个是奇数，不妨令 $a$ 为奇数，那么 $b$ 为偶数且 $c$ 为奇数（如果 $a$ 和 $b$ 都是奇数，那么 $c^2$ 会是偶数，那么 $c$ 也会是偶数，那么 $4 \mid c^2$，而 $a^2 + b^2 \bmod 4 = 2$，矛盾）。

我们得到 $c^2 - a^2 = b^2$，因此 $(c-a)(c+a) = b^2$，即 $\dfrac{c+a}{b} = \dfrac{b}{c-a}$。$\dfrac{c+a}{b}$ 显然为有理数，设其最简形式为 $\dfrac{\varphi }{\lambda}$。因此 $\dfrac{c-a}{b} = \dfrac{\lambda}{\varphi }$。我们有：

\[\frac{c}{b} + \frac{a}{b} = \frac{\varphi }{\lambda}, \quad \quad \frac{c}{b} - \frac{a}{b} = \frac{\lambda}{\varphi } \]
解出 $\dfrac{c}{b}$ 和 $\dfrac{a}{b}$ 分别为：

\[\frac{c}{b} = \frac{1}{2}\left(\frac{\varphi }{\lambda} + \frac{\lambda}{\varphi }\right) = \frac{\varphi ^2 + \lambda^2}{2\varphi \lambda}, \quad \quad \frac{a}{b} = \frac{1}{2}\left(\frac{\varphi }{\lambda} - \frac{\lambda}{\varphi }\right) = \frac{\varphi ^2 - \lambda^2}{2\varphi \lambda}. \]
由于 $\varphi \perp \lambda$，故它们不能同为偶数。若它们同为奇数，则 $\dfrac{\varphi ^2 - \lambda^2}{2\varphi \lambda}$ 的分子将是 $4$ 的倍数，而分母关于 $2$ 的因子有且仅有一个 $2$，导出 $a$ 必为偶数，和我们假设 $a$ 为奇数矛盾。因此，$\lambda$ 和 $\varphi $ 中恰有一个偶数，所以 $\varphi ^2 \pm \lambda^2$ 为奇数。因此，这些分数是最简分数（如果有一个奇质数 $p$ 为分子分母的公因数，由于 $\lambda$ 和 $\varphi $ 的奇偶性，只能整除 $\lambda$ 或 $\varphi $ 其中一个，那么就不可以整除分子 $\varphi ^2 \pm \lambda^2$，矛盾）。由此将分子与分子相等，分母与分母相等，得到欧几里得公式：

\[a = \varphi ^2 - \lambda^2, \quad b = 2\varphi \lambda, \quad c = \varphi ^2 + \lambda^2 \]

我们可以 $\Theta(\sqrt{n})$ 地枚举 $\varphi$，再 $\mathcal{O}(\sqrt{n})$ 的枚举 $\lambda \lt \varphi$，这也说明了 $a, b, c \leq n$ 的「本原三元组」是 $\Theta(\sqrt{n})\cdot\mathcal{O}(\sqrt{n}) = \mathcal{O}(n)$ 的。事实上，这是一个较松的上界。

根据 $\varphi ^2 + \lambda^2 \leq c = k \cdot(\varphi ^2 + \lambda^2) \leq n$，得到 $\lambda \leq \sqrt{n - \varphi ^2}$。同时结合 $\lambda \lt \varphi$。得到枚举 $\lambda$ 更精确的时间复杂度是 $\Theta \left(\min \left\{ \sqrt{n - \varphi ^2}, \varphi - 1 \right\}\right)$。

由于 $\min \left\{ \sqrt{n - \varphi ^2}, \varphi-1 \right\} \leq \varphi-1$，我们不妨按照 $\varphi - 1$ 计算上界。

此时内层为 ${\displaystyle \mathcal{O}\left(\sum_{\lambda=1}^{\varphi - 1} \dfrac{n}{\varphi ^2 + \lambda^2}\right) \leq \mathcal{O}\left(\sum_{\lambda=1}^{\varphi - 1} \dfrac{n}{\varphi ^2}\right) = \mathcal{O}\left(\dfrac{n}{\varphi}\right)}$。其中第二步放缩是在分母中，直接去掉了 $\lambda^2$ 这一项。我之前推的时候因为 $\lambda \lt \varphi$，把分母看做 $2\lambda^2$，然后省略常数什么的，得到的上界是很松的 $\Theta(n\sqrt{n})$，疑惑了好久。

于是就能得到总的时间复杂度的式子最后长这样：

\[\begin{aligned} &\quad\ \mathcal{O}\left(\sum_{\varphi=1}^{\sqrt{n}} \sum_{\lambda=1}^{\min \left\{ \sqrt{n - \varphi ^2}, \varphi - 1 \right\}} \dfrac{n}{\varphi ^2 + \lambda^2} \right) \\ & \leq \mathcal{O}\left(\sum_{\varphi=1}^{\sqrt{n}} \sum_{\lambda=1}^{\varphi-1} \dfrac{n}{\varphi ^2 + \lambda^2} \right) \\ & \leq \mathcal{O}\left(\sum_{\varphi=1}^{\sqrt{n}} \frac{n}{\varphi} \right) \\ & \leq \mathcal{O}\left(n\sum_{\varphi=1}^{n} \frac{1}{\varphi} \right) \\ & \leq \mathcal{O}\left(n \log n \right) \\ \end{aligned} \]

我们使用 $\Theta(n \log n)$ 的算法找出了 $n$ 以内所有「三元组」。话说回来，生成出来有什么用呢？我们发现一个斜着的正方形，可以通过「改斜归正」，四条边分别往外做四个全等的直角三角形，且三角形三边为我们求出的「三元组」，变成一个正的正方形。为了方便讨论，我们可以特殊地令「三元组」$(a, b, c)$ 其中可以有 $0$，也就是本来就是正的正方形，也可以这样操作。

改斜归正

注意到，对于 $a, b \neq 0$，交换 $a, b$，也就是将上图左右翻转，也是合法的。我们现在考虑 $(a, b, c)$ 对整个平面哪些点有贡献。我们不妨钦定询问的点，作为这些正方形的某一顶点，然后考虑边界情况，可以得到下图。

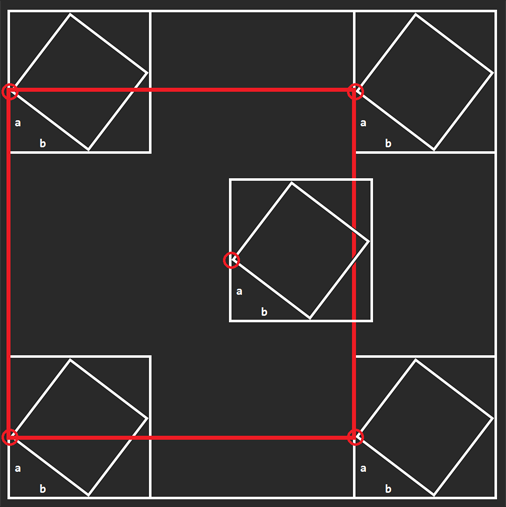
对某一矩形的贡献

发现，如果询问的点在红色矩形内，就可以用这组 $(a, b, c)$ 做出以 $(x, y)$ 为左顶点的合法正方形。可以离线下来做扫描线。其它 $3$ 个端点类似处理即可。总共 $4$ 次扫描线。或者由于图形很强的对称性，不用做 $4$ 次扫描线，只做 $1$ 次来优化常数，读者自行优化不难。

时间复杂度 $\Theta(n \log^2n + q \log n)$。

代码

#include <cstdio>
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 100010, Q = 500010;

int n, q, ans[Q];
vector<pair<int, int>> line[N], qx[N], qy[N], triple;

struct Bit_Tree {
    static constexpr inline int lowbit(int x) {
        return x & -x;
    }
    int tree[N];
    inline void clear() {
        memset(tree + 1, 0x00, sizeof (int) * (n));
    }
    inline void modify(int p, int v) {
        for (int i = p; i <= n; i += lowbit(i))
            tree[i] += v;
    }
    inline void modify(int l, int r, int v) {
        modify(l, v), modify(r + 1, -v);
    }
    inline int query(int p) {
        int res = 0;
        for (int i = p; i; i -= lowbit(i))
            res += tree[i];
        return res;
    }
} yzh;

signed main() {
    #ifndef XuYueming
    freopen("WSDR.in", "r", stdin);
    freopen("WSDR.out", "w", stdout);
    #endif
    scanf("%*d%d%d", &n, &q);
    for (int i = 1; i * i <= n; ++i)
    for (int j = (i & 1) ^ 1; i * i + j * j <= n && j < i; j += 2)
        if (__gcd(i, j) == 1) {
            for (int k = 1; k * (i * i + j * j) <= n; ++k) {
                int a = k * (i * i - j * j), b = k * (2 * i * j);
                if (a + b + 1 <= n) {
                    triple.emplace_back(a, b);
                    if (b) triple.emplace_back(b, a);
                    // 交换 (a, b)
                }
            }
        }
    for (int i = 1, x, y; i <= q; ++i) {
        scanf("%d%d", &x, &y);
        qx[x].emplace_back(y, i);
        qy[y].emplace_back(x, i);
    }
    
    for (auto& [a, b]: triple) line[n - a - b].emplace_back(1 + a, n - b);
    for (int i = n; i >= 1; --i) {
        for (auto& [l, r]: line[i]) yzh.modify(l, r, 1);
        for (auto& [y, p]: qx[i]) ans[p] += yzh.query(y);
    }
    
    yzh.clear();
    for (int i = 1; i <= n; ++i) line[i].clear();
    for (auto& [a, b]: triple) line[1 + a + b].emplace_back(1 + b, n - a);
    for (int i = 1; i <= n; ++i) {
        for (auto& [l, r]: line[i]) yzh.modify(l, r, 1);
        for (auto& [y, p]: qx[i]) ans[p] += yzh.query(y);
    }
    
    yzh.clear();
    for (int i = 1; i <= n; ++i) line[i].clear();
    for (auto& [a, b]: triple) line[1 + a + b].emplace_back(1 + a, n - b);
    for (int i = 1; i <= n; ++i) {
        for (auto& [l, r]: line[i]) yzh.modify(l, r, 1);
        for (auto& [y, p]: qy[i]) ans[p] += yzh.query(y);
    }
    
    yzh.clear();
    for (int i = 1; i <= n; ++i) line[i].clear();
    for (auto& [a, b]: triple) line[n - a - b].emplace_back(1 + b, n - a);
    for (int i = n; i >= 1; --i) {
        for (auto& [l, r]: line[i]) yzh.modify(l, r, 1);
        for (auto& [y, p]: qy[i]) ans[p] += yzh.query(y);
    }
    
    for (int i = 1; i <= q; ++i)
        printf("%d\n", ans[i]);
    return 0;
}