P8907 [USACO22DEC] Making Friends P

SunnyYuan的博客 / 2024-09-21 / 原文

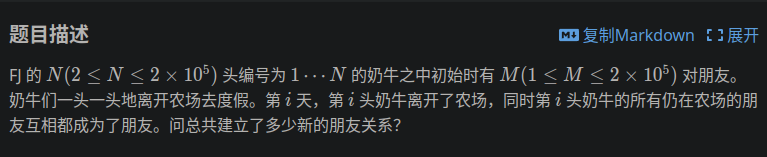
题目

思路

我们可以统计出所有点对之间应该有的边的数量然后再减去之前的 $m$。

对于每个点维护一个集合，统计该点应该连接的点。

对于每条初始边，我们将其看作从编号小的点连向编号大的点，并在编号小的集合中放入编号大的点。

处理删除 $i$ 点操作，答案加上目前集合 $i$ 的大小，表示 $i$ 在之前一定会与这些点相连；然后求出目前集合 $i$ 的编号最小的点 $x$，将所有 $i$ 集合中的点删除 $x$ 后放入集合 $x$ 中，表示 $x$ 会与这些点相连。

最后将答案减去 $m$ 即可。

这种做法聪明之处在于，它完美地利用了删点从小到大的性质，将本应该在点 $i$ 删除时处理的点对，延迟处理。

代码

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 200010;

int n, m;
set<int> g[N];

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u, v;
        cin >> u >> v;
        g[min(u, v)].insert(max(u, v));
    }

    int ans = 0;
    for (int i = 1; i <= n; i++) {
        if (!g[i].size()) continue;
        ans += g[i].size();
        int x = *g[i].begin();
        g[i].erase(g[i].begin());
        if (g[i].size() > g[x].size()) swap(g[x], g[i]);
        for (auto y : g[i]) g[x].insert(y);
    }
    ans -= m;
    cout << ans << '\n';
    return 0;
}