从kmp到AC自动机
知道kmp的请跳过这一段
找到最清晰的解析
kmp
我看了约114514个解析才搞懂
如何求next
首先,next[i]本应表示0~i的字符串的最长相同前缀后缀的长度。
不过为了方便匹配,实际可以存最长相同前缀后缀时前缀最后一个的地址
听起来好绕
那这么说吧:
例如串
abaabaabaab
next[0]=-1 肯定找不到
next[1]=-1 因为第一个前缀是a,它是b
next[2]=0 因为第一个前缀是a,它是a
next[3]=0 因为第一个前缀是a,它是a?
wait!不一样的点来啦!
先偷窥一下匹配的代码:
for (int i=1;i<m;i++){
int j=next[i-1];
while ((s[j+1]!=s[i])&&(j>=0))j=next[j];
if (s[j+1]==s[i]) next[i]=j+1;
else next[i]=-1;
}
也就是
a先问了它旁边那个,发现它匹配到了0
然后他也蠢蠢欲动
但下个是b
所以他的j被打到了next[2]=-1
然后循环没了
这时,他毫不惊奇地发现下一个是a
于是他就匹配上了(合理)
next[4]=1
因为它前面已经匹配到了,所以它可能是 前面匹配到的 前缀的地址+1的 那个字母
听起来还是好绕
说白了,它可以是
b先问了它旁边那个,发现它匹配到了0
然后他也蠢蠢欲动
发现下个是b
所以循环没了
这时,他毫不(是真的)惊奇地发现下一个是b
于是
abaab(内两b匹配上了)
理解了吧?
剩下的自己推,别问我
那么,现在烤馍片完成了,该做什么呢
next的作用
以下搬运自dalao题解,此处F[i]指next[i]+1
我们还是先给出一个例子:
A="abaabaabbabaaabaabbabaab"
B="abaabbabaab"
当然读者可以通过手动模拟得出只有一个地方匹配
abaabaabbabaaabaabbabaab
我们再用i表示当前A串要匹配的位置(即还未匹配),j表示当前B串匹配的位置(同样也是还未匹配),补充一下,若i>0则说明i-1是已经匹配的啦(j同理)。
首先我们还是从0开始匹配:
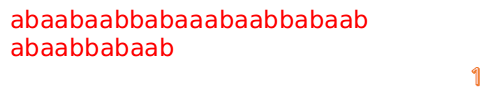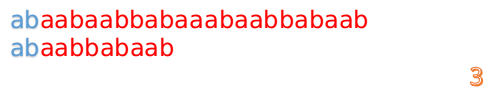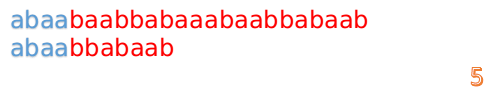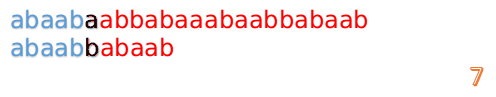
此时,我们发现,A的第5位和B的第5位不匹配(注意从0开始编号),此时i=5,j=5,那么我们看F[j-1]的值:
F[5-1]=2;
这说明我们接下来的匹配只要从B串第2位开始(也就是第3个字符)匹配,因为前两位已经是匹配的啦,具体请看图:
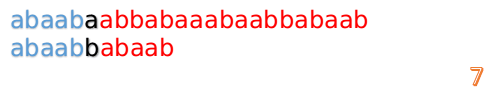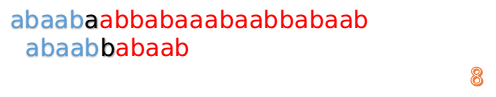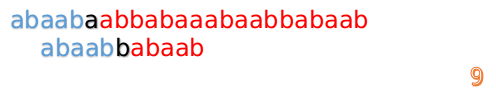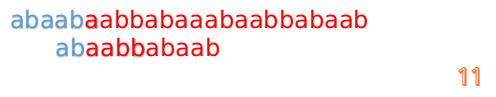
然后再接着匹配:
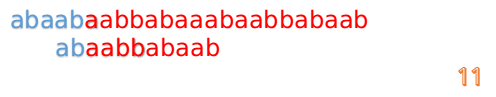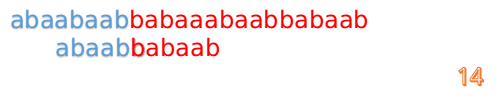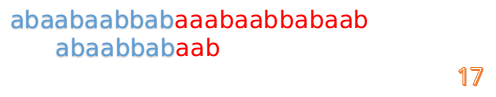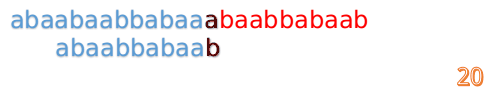
我们又发现,A串的第13位和B串的第10位不匹配,此时i=13,j=10,那么我们看F[j-1]的值:
F[10-1]=4
这说明B串的03位是与当前(i-4)(i-1)是匹配的,我们就不需要重新再匹配这部分了,把B串向后移,从B串的第4位开始匹配:
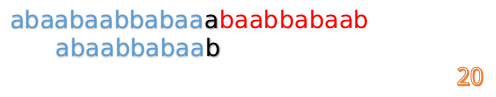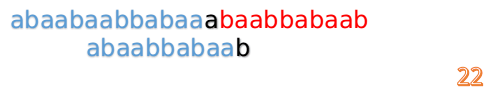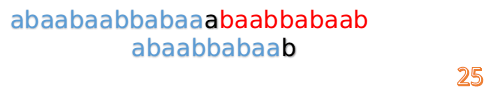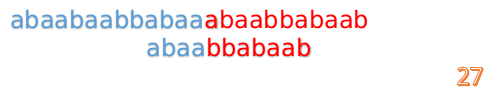
这时我们发现A串的第13位和B串的第4位依然不匹配

此时i=13,j=4,那么我们看F[j-1]的值:
F[4-1]=1
这说明B串的第0位是与当前i-1位匹配的,所以我们直接从B串的第1位继续匹配:

但此时B串的第1位与A串的第13位依然不匹配

此时,i=13,j=1,所以我们看一看F[j-1]的值:
F[1-1]=0
好吧,这说明已经没有相同的前后缀了,直接把B串向后移一位,直到发现B串的第0位与A串的第i位可以匹配(在这个例子中,i=13)

再重复上面的匹配过程,我们发现,匹配成功了!

这就是KMP算法的过程。
另外强调一点,当我们将B串向后移的过程其实就是i++,而当我们不动B,而是匹配的时候,就是i++,j++,这在后面的代码中会出现,这里先做一个说明。
最后来一个完整版的(dalao:话说做这些图做了好久啊!!!!):
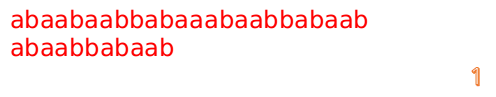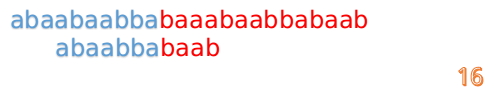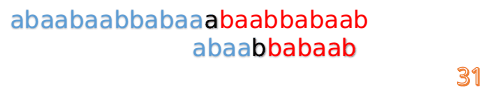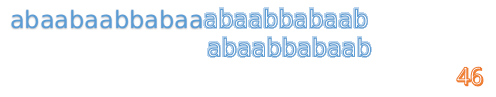
kmp例题代码实现:
#include <bits/stdc++.h>
using namespace std;
string s1,s2;
int n,m,i,j,_next[1000010];
int main(){
cin>>s1>>s2;
n=s2.size();
m=s1.size();
_next[0]=-1;
for (i=1;i<n;i++){
j=_next[i-1];
while ((s2[j+1]!=s2[i])&&(j>=0))j=_next[j];
if (s2[j+1]==s2[i]) _next[i]=j+1;
else _next[i]=-1;
}
i=0;j=0;
while (i<m) {
if (s1[i]==s2[j]) {
i++;
j++;
if(j==n)cout<<i-n+1<<endl,j=_next[j-1]+1;
}else{
if (j==0)i++;
else j=_next[j-1]+1;
}
}
for (i=0;i<n;i++){
cout<<_next[i]+1<<" ";
}
return 0;
}
c,怎么这么难调
知道Trie的请跳过这一段
网上的解析
Trie
大概论述一下过程:
- 选定要加入到Trie树中的字符串
- 从根节点开始依次判断当前结点的子节点中是否包含下一个字符
- 如果包含,则直接访问,重复第2步
- 否则,则建立这个结点,继续重复第2步
- 若进行第2步时已经到达了最后一个字符,则直接结束
那么,我们来举个例子
假如,我要构建成字典树的单词是her hen hers say said
最终构建完的字典树就长这样:
root
/ \
h s
/ \
e a
/ \ / \
r n y i
| |
s d
然而我们并不知道这些东西分别代表那些字符串
于是,我们对每个字符串的结尾所在的那个节点加个标记。
于是乎,我们从根节点开始,一层层依次遍历,当读入到一个加了标记的结点时,一路读到的字符连成的字符串便是原来需要储存的字符串
那么,至于怎么加入一个串呀。。。
我们也来演示一下吧、。。。
比如当前这样子:
root
/ \
h s
/ \
e a
/ \ /
r n y
|
s
其他的串都已经加入,我们现在需要加入字符串said
那么,我们从根节点开始
ro_ot(用_表示当前节点)
/ \
h s
/ \
e a
/ \ /
r n y
|
s
发现根节点的子节点里面存在s这个字符结点
把一个指针移动过去,继续找接下来的字符
root
/ \
h _s
/ \
e a
/ \ /
r n y
|
s
接着,我们惊奇的发现a也存在了,于是继续遍历
root
/ \
h s
/ \
e _a
/ \ /
r n y
|
s
这个时候,却发现当前结点不存在一个i结点,那么,我们就手动的造一个i结点出来
root
/ \
h s
/ \
e a
/ \ / \
r n y i
|
s
同理:
root
/ \
h s
/ \
e a
/ \ / \
r n y i
| |
s d
OK,上代码!
#include <bits/stdc++.h>
using namespace std;
int n,end=0;
vector<int> fa(100005),son(100005),nth(100005),sa[26](100005);//窝喜欢用vector,别喷窝啊……
void build(int where,string s,int now){
if(now>=s.size())return;
if(son[where]&(1<<int(c[now]-'a')))build(sa[int(c[now]-'a')][where],s,now+1);
else{
end++;
fa[end]=where;
son[where]|=(1<<int(c[now]-'a'));
sa[int(c[now]-'a')][where]=end;
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
while(cin>>n&&n){
fa=nth;
son=nth;
fail=nth;
end=0;
for(int i=1;i<=n;i++){
string s;
cin>>s;
build(0,s,0);
}
}
return 0;
}