The American University in Cairo CSEA End of Winter Break Contest 2023

h-rm / 2024-08-31 / 原文

链接：https://codeforces.com/gym/104168

$\\$

A Divisor Difference

签到，输出 $n-1$ 即可，复杂度 $O(1)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    cin >> n;

    cout << n - 1 << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

B1 Longest Common Suffix

签到，从后往前枚举即可，复杂度 $O(min(len(a),len(b)))$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    cin >> n >> m;

    string a, b;
    cin >> a >> b;

    if (n < m) {
        swap(n, m);
        swap(a, b);
    }

    for (int i = n - 1; i >= 0; i--) {
        if (a[i] != b[i - n + m]) {
            cout << n - 1 - i << endl;
            return;
        }
    }

    cout << m << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

B2 Mina and Ayman

签到，逐位模拟即可，复杂度 $O(nlogn)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    int x;
    cin >> n >> x;

    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    vector<int> sum(32, 0);

    for (int i = 0; i < n; i++) {
        if (a[i] == -1) {
            continue;
        }
        for (int j = 0; j < 31; j++) {
            sum[j] += (a[i] >> j) & 1;
        }
    }

    int ans = 0;

    for (int j = 0; j < 31; j++) {
        if ((sum[j] & 1) != ((x >> j) & 1)) {
            ans += 1 << j;
        }
    }

    cout << ans << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

C1 Sets and Integers

签到，全部做 $bitwise OR$ 即可，复杂度 $O(n)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    cin >> n;

    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    int ans = 0;

    for (auto &c: a) {
        ans |= c;
    }

    cout << ans << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

C2 Flipping Cards

签到，简单贪心，复杂度 $O(nlogn)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    cin >> n >> k;

    vector<pair<i64, i64>> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i].first;
    }
    for (int i = 0; i < n; i++) {
        cin >> a[i].second;
    }

    sort(a.begin(), a.end(), [](pair<i64, i64> p, pair<i64, i64> q) {
        return p.second - p.first > q.second - q.first;
    });

    i64 ans = 0;

    int j = k;
    for (int i = 0; i < k; i++) {
        if (a[i].second < a[i].first) {
            j = i;
            break;
        }
        ans += a[i].second;
    }

    for (int i = j; i < n; i++) {
        ans += a[i].first;
    }

    cout << ans << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

C3 Nested Sum (Easy Version)

签到，一维前缀和，复杂度 $O(n)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    cin >> n;

    vector<i64> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    vector<i64> sum(n + 1, 0);
    for (int i = 1; i <= n; i++) {
        sum[i] = sum[i - 1] + a[i];
    }

    i64 ans = 0;

    for (int i = 1; i <= n; i++) {
        ans += a[i] * (sum[n] - sum[i]);
    }

    cout << ans << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

C4 Polynomial Convolution

签到，按系数枚举即可，复杂度 $O(n)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    cin >> n >> m >> k;

    vector<i64> a(n), b(m);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    for (int i = 0; i < m; i++) {
        cin >> b[i];
    }

    i64 ans = 0;

    for (int i = 0; i <= min(k, n - 1); i++) {
        if (k - i > m - 1) {
            continue;
        }
        ans += a[i] * b[k - i];
    }

    cout << ans << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

D1 Looks Divisible To Me

签到，本质是因数分解，复杂度 $O(\sqrt{n} \cdot logn)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    cin >> n;

    vector<int> res;
    for (int i = 1; i * i <= n; i++) {
        if (n % i == 0) {
            res.emplace_back(i);
            res.emplace_back(n / i);
        }
    }

    sort(res.begin(), res.end());
    res.erase(unique(res.begin(), res.end()), res.end());

    for (int i = 0; i < res.size(); i++) {
        cout << res[i] << " \n"[i == res.size() - 1];
    }

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

D2 Nested Sum (Hard Version)

签到，二维前缀和，复杂度 $O(n)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

class Z {
    using i64 = long long;
    static const i64 Mod = 1000000007;
public:
    i64 num;
    Z() = default;
    Z(i64 _num) : num((_num % Mod + Mod) % Mod) {}
    i64 val() const {
        return num;
    }
    Z &operator = (i64 b) {
        return *this = Z(b);
    }
    friend bool operator < (Z a, Z b) {
        return a.num < b.num;
    }
    friend bool operator >(Z a, Z b) {
        return a.num > b.num;
    }
    friend bool operator <=(Z a, Z b) {
        return a.num <= b.num;
    }
    friend bool operator>=(Z a, Z b) {
        return a.num >= b.num;
    }
    friend bool operator==(Z a, Z b) {
        return a.num == b.num;
    }
    friend Z operator + (Z a, Z b) {
        return Z((a.num + b.num) % Mod);
    }
    friend Z &operator += (Z &a,Z b) {
        return a = a + b;
    }
    friend Z operator + (Z a, i64 b) {
        return a + Z(b);
    }
    friend Z &operator += (Z &a, i64 b) {
        return a = a + b;
    }
    friend Z &operator ++ (Z &a) {
        return a += 1;
    }
    friend Z operator ++ (Z &a, int) {
        Z copy(a);
        a += 1;
        return copy;
    }
    friend Z operator - (Z a, Z b) {
        return Z(((a.num - b.num) % Mod + Mod) % Mod);
    }
    friend Z &operator -= (Z &a, Z b) {
        return a = a - b;
    }
    friend Z operator - (Z a, i64 b) {
        return a - Z(b);
    }
    friend Z &operator -= (Z &a, i64 b) {
        return a = a - b;
    }
    friend Z &operator -- (Z &a) {
        return a -= 1;
    }
    friend Z operator -- (Z &a, int) {
        Z copy(a);
        a -= 1;
        return copy;
    }
    friend Z operator * (Z a, Z b) {
        return Z((long long)a.num * b.num % Mod);
    }
    friend Z &operator *= (Z &a, Z b) {
        return a = a * b;
    }
    friend Z operator * (Z a, i64 b) {
        return a * Z(b);
    }
    friend Z &operator *= (Z &a, i64 b) {
        return a = a * b;
    }
    Z inv() {
        i64 ans = 1;
        i64 a = num;
        i64 b = Mod - 2; 
        while (b) {
            if (b & 1) ans = ans * a % Mod;
            a = a * a % Mod;
            b >>= 1;
        }
        return Z(ans);
    }
    friend Z operator / (Z a, Z b) {
        return a * b.inv();
    }
    friend Z &operator /= (Z &a, Z b) {
        return a = a / b;
    }
    friend Z operator / (Z a, i64 b) {
        return a / Z(b);
    }
    friend Z &operator /= (Z &a, i64 b) {
        return a = a / b;
    }
    friend std::istream &operator>>(std::istream &is, Z &a) {
        int v;
        is >> v;
        a = Z(v);
        return is;
    }
    friend std::ostream &operator<<(std::ostream &os, const Z &a) {
        return os << a.val();
    }
};

void solve() {
    cin >> n;

    vector<i64> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    vector<Z> sum(n + 1, 0);
    vector<Z> C(n + 1, 0), D(n + 1, 0);
    for (int i = 1; i <= n; i++) {
        sum[i] = sum[i - 1] + a[i];
    }

    for (int i = 1; i <= n; i++) {
        C[i] = a[i] * (sum[n] - sum[i]);
    }

    for (int i = 1; i <= n; i++) {
        D[i] = D[i - 1] + C[i];
    }

    Z ans = 0;

    for (int i = 1; i <= n; i++) {
        ans += a[i] * (D[n] - D[i]);
    }

    cout << ans << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

D3 Rotating Strings

由于字符串可以重新排列（如果不能的话直接套个 $Hash$ 暴力就可以），数一下每个字符出现的次数，若其 $gcd$ 为 $1$，说明不能被分成若干个相同的集合，答案为 $0$，

否则答案为 $($ 集合数$-1) \times$ 集合长度，复杂度为常数。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    string s;
    cin >> n >> s;

    vector<int> sum(26, 0);

    for (auto &c: s) {
        sum[c - 'a']++;
    }

    int u = 1;
    for (int i = 0; i < 26; i++) {
        if (sum[i]) {
            // cerr << sum[i] << " ";
            u = sum[i];
            for (int j = i + 1; j < 26; j++) {
                if (sum[j]) {
                    // cerr << sum[j] << " ";
                    u = __gcd(u, sum[j]);
                }
            }
            break;
        }
    }

    // cerr << endl;

    if (u == 1) {
        cout << 0 << endl;

    } else {
        int ans = 0;
        for (auto &c: sum) {
            ans += c / u;
        }

        assert(n % ans == 0);
        cout << n - ans << endl;
    }

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

D4 The Dilworth Tree

容易发现最大集合的大小实际上等于叶子结点的数量，并且对于每个子结点和叶子结点，如果存在一条单向的链，则可选取该链上的任意结点，

如图所示，叶子结点 $7$ 对应的链的结点的数量为 $4$，叶子结点 $2,3$ 对应的链的结点数量为 $1$，则集合数量为 $4 \times 1 \times 1 = 4$。

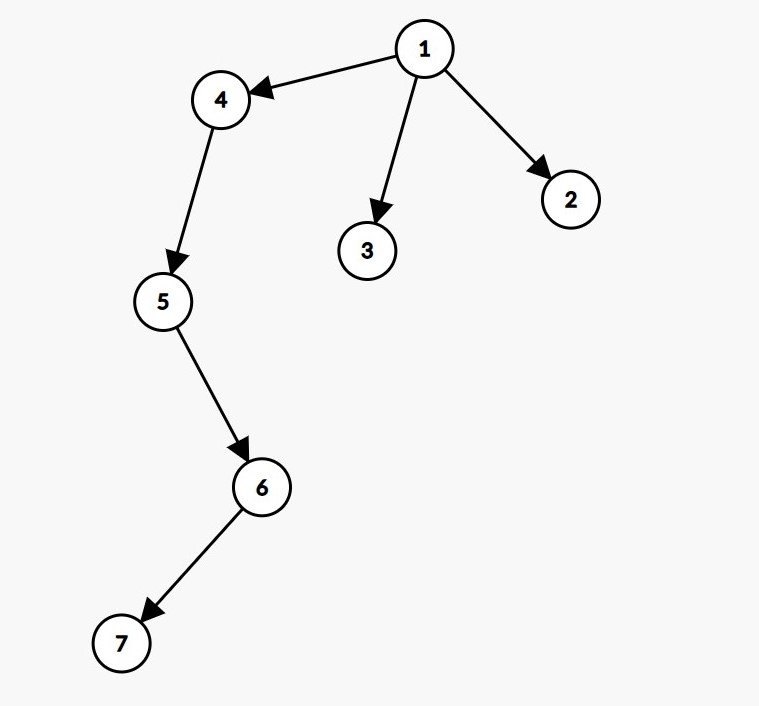
设第 $i$ 个叶子结点对应链的编号为 $p_i$，答案即为

\[\prod_{p_i \in Tree}{number \ of \ vertex \ in \ p_i} \]

复杂度 $O(n)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

class Z {
    using i64 = long long;
    static const i64 Mod = 1000000007;
public:
    i64 num;
    Z() = default;
    Z(i64 _num) : num((_num % Mod + Mod) % Mod) {}
    i64 val() const {
        return num;
    }
    Z &operator = (i64 b) {
        return *this = Z(b);
    }
    friend bool operator < (Z a, Z b) {
        return a.num < b.num;
    }
    friend bool operator >(Z a, Z b) {
        return a.num > b.num;
    }
    friend bool operator <=(Z a, Z b) {
        return a.num <= b.num;
    }
    friend bool operator>=(Z a, Z b) {
        return a.num >= b.num;
    }
    friend bool operator==(Z a, Z b) {
        return a.num == b.num;
    }
    friend Z operator + (Z a, Z b) {
        return Z((a.num + b.num) % Mod);
    }
    friend Z &operator += (Z &a,Z b) {
        return a = a + b;
    }
    friend Z operator + (Z a, i64 b) {
        return a + Z(b);
    }
    friend Z &operator += (Z &a, i64 b) {
        return a = a + b;
    }
    friend Z &operator ++ (Z &a) {
        return a += 1;
    }
    friend Z operator ++ (Z &a, int) {
        Z copy(a);
        a += 1;
        return copy;
    }
    friend Z operator - (Z a, Z b) {
        return Z(((a.num - b.num) % Mod + Mod) % Mod);
    }
    friend Z &operator -= (Z &a, Z b) {
        return a = a - b;
    }
    friend Z operator - (Z a, i64 b) {
        return a - Z(b);
    }
    friend Z &operator -= (Z &a, i64 b) {
        return a = a - b;
    }
    friend Z &operator -- (Z &a) {
        return a -= 1;
    }
    friend Z operator -- (Z &a, int) {
        Z copy(a);
        a -= 1;
        return copy;
    }
    friend Z operator * (Z a, Z b) {
        return Z((long long)a.num * b.num % Mod);
    }
    friend Z &operator *= (Z &a, Z b) {
        return a = a * b;
    }
    friend Z operator * (Z a, i64 b) {
        return a * Z(b);
    }
    friend Z &operator *= (Z &a, i64 b) {
        return a = a * b;
    }
    Z inv() {
        i64 ans = 1;
        i64 a = num;
        i64 b = Mod - 2; 
        while (b) {
            if (b & 1) ans = ans * a % Mod;
            a = a * a % Mod;
            b >>= 1;
        }
        return Z(ans);
    }
    friend Z operator / (Z a, Z b) {
        return a * b.inv();
    }
    friend Z &operator /= (Z &a, Z b) {
        return a = a / b;
    }
    friend Z operator / (Z a, i64 b) {
        return a / Z(b);
    }
    friend Z &operator /= (Z &a, i64 b) {
        return a = a / b;
    }
    friend std::istream &operator>>(std::istream &is, Z &a) {
        int v;
        is >> v;
        a = Z(v);
        return is;
    }
    friend std::ostream &operator<<(std::ostream &os, const Z &a) {
        return os << a.val();
    }
};

void solve() {
    cin >> n;

    vector<vector<int>> adj(n + 1);

    for (int i = 2; i <= n; i++) {
        int x;
        cin >> x;

        adj[x].emplace_back(i);
    }

    int mx = 0;
    auto dfs = [&](auto &&self, int u) -> int {
        if (!adj[u].size()) {
            return 1;
        }
        int cur = 0;
        for (auto c: adj[u]) {
            cur += self(self, c);
        }
        return cur;
    };

    mx += dfs(dfs, 1);

    const int N = __lg(n) + 2;
    Z ans = 1;

    auto dfs2 = [&](auto &&self, int u, int cur) -> void {
        if (adj[u].size() > 1) {
            for (auto c: adj[u]) {
                self(self, c, 1);
            }
        } else if (adj[u].size() == 1) {
            self(self, adj[u][0], cur + 1);
        } else {
            ans *= cur;
        }
    };

    dfs2(dfs2, 1, 1);

    cout << mx << " " << ans << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

E1 Blips and Chitz

考虑 $DP(i, \ j)$ 表示遍历到下标为 $i$ 的物品时，物品总重量 $mod \ m = j$ 时的最大价值，转移方程是不难想的，但需要注意在枚举状态时，判断该状态是否合法。判断的方法也很简单，

若当前枚举的重量为 $0$，则状态一定合法，否则当 $DP(i, \ j) > 0$ 时合法，即

\[choose \begin{cases} j = 0 \ \ or \ \ DP(i, \ j) > 0: \ \ \ DP(i, \ (j + w_i) \ mod \ m) = max(DP(i - 1, \ (j + w_i) \ mod \ m) , DP(i - 1, \ j) + v_i) \\ otherwise: \ \ \ DP(i, \ w_i) = max(DP(i - 1, \ w_i), DP(i - 1, \ 0) + v_i) \end{cases}\]

\[not \begin{cases} j = 0 \ \ or \ \ DP(i, \ j) > 0: \ \ \ DP(i, \ j) = max(DP(i, \ j) , DP(i - 1, \ j)) \\ otherwise: \ \ \ DP(i, \ 0) = max(DP(i, \ 0), DP(i - 1, \ 0)) \end{cases}\]

若下标从 $0$ 开始，答案即为 $DP(n - 1, 0)$，复杂度 $O(nm)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    cin >> n >> m;

    vector<i64> w(n), p(n);
    for (int i = 0; i < n; i++) {
        cin >> w[i];
        w[i] %= m;
    }
    for (int i = 0; i < n; i++) {
        cin >> p[i];
    }

    vector<vector<i64>> dp(n, vector<i64> (m, 0));

    dp[0][w[0]] = p[0];
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (j && dp[i - 1][j]) {
                dp[i][(j + w[i]) % m] = max(dp[i - 1][(j + w[i]) % m], dp[i - 1][j] + p[i]);
                dp[i][j] = max(dp[i][j], dp[i - 1][j]);

            } else {
                dp[i][w[i]] = max(dp[i - 1][w[i]], dp[i - 1][0] + p[i]);
                dp[i][0] = max(dp[i][0], dp[i - 1][0]);
            }
        }
    }

    cout << dp[n - 1][0] << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

E2 Make Them Equivalent

分组之后选择每组的中位数作为目标值即可，复杂度 $O(\frac{n}{k} \cdot (logn - logk))$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    i64 x;
    cin >> n >> k >> x;

    vector<i64> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    vector<vector<int>> div;
    vector<bool> vis(n + 1, false);

    for (int i = 1; i <= n; i++) {
        if (vis[i]) {
            continue;
        }
        vector<int> use;
        for (int j = i; j <= n; j += k) {
            use.emplace_back(a[j]);
            vis[j] = true;
        }
        sort(use.begin(), use.end());
        div.emplace_back(use);
    }

    i64 ans = 0;

    for (auto &c: div) {
        if (c.size() == 1) {
            continue;
        }
        auto e = c[c.size() / 2];
        for (auto &d: c) {
            ans += abs(d - e) * x;
        }
    }

    cout << ans << endl;

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}

$\\$

F Proofy and the cat

考虑二分答案，每次 $check$ 做一次 $DFS$ ，由于可以从任意结点出发，可以将所有结点连到 $0$ 结点，然后以 $0$ 结点为起点，复杂度 $O(nlogn)$。

点击查看代码

#pragma GCC optimize("unroll-loops, Ofast")
#include<bits/stdc++.h>

using namespace std;
using i64 = long long;
#define endl '\n'
#define lowbit(x) x & -x
constexpr i64 Mod = 1000000007;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
i64 n, m, k;

void init() {}

void solve() {
    cin >> n >> k;

    vector<i64> a(n + 1, 0);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    vector<vector<int>> adj(n + 1);
    vector<int> p(n + 1);

    for (int i = 2; i <= n; i++) {
        cin >> p[i];
        adj[p[i]].emplace_back(i);
    }

    map<pair<int, int>, i64> w;
    for (int i = 2; i <= n; i++) {
        cin >> m;
        if (w.contains({p[i], i})) {
            w[{p[i], i}] = w[{i, p[i]}] = min(w[{p[i], i}], m);

        } else {
            w[{p[i], i}] = w[{i, p[i]}] = m;
        }
    }

    for (int i = 1; i <= n; i++) {
        adj[0].emplace_back(i);
        w[{0, i}] = w[{i, 0}] = 0;
    }

    bool check = false;
    auto dfs = [&](auto &&self, int u, i64 cur, i64 tar) -> void {
        if (cur >= k) {
            check = true;
            return;
        }
        if (check) {
            return;
        }
        for (auto c: adj[u]) {
            if (w[{c, u}] > tar) {
                continue;
            }
            self(self, c, cur + a[c], tar);
        }
    };

    i64 l = 0, r = 1e9;
    while (l <= r) {
        i64 mid = l + r >> 1;

        check = false;
        dfs(dfs, 0, 0, mid);

        if (check) {
            r = mid - 1;
        } else {
            l = mid + 1;
        }
    }

    if (l < 1000000001) {
        cout << l << endl;
        
    } else {
        cout << -1 << endl;
    }

}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 

    init();

    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
 
    return 0; 
}