接上一篇

T1

链接：

https://www.luogu.com.cn/problem/P2196

[NOIP1996 提高组] 挖地雷

题目描述

在一个地图上有 \(N\ (N \le 20)\) 个地窖，每个地窖中埋有一定数量的地雷。同时，给出地窖之间的连接路径。当地窖及其连接的数据给出之后，某人可以从任一处开始挖地雷，然后可以沿着指出的连接往下挖（仅能选择一条路径），当无连接时挖地雷工作结束。设计一个挖地雷的方案，使某人能挖到最多的地雷。

输入格式

有若干行。

第 \(1\) 行只有一个数字，表示地窖的个数 \(N\)。

第 \(2\) 行有 \(N\) 个数，分别表示每个地窖中的地雷个数。

第 \(3\) 行至第 \(N+1\) 行表示地窖之间的连接情况：

第 \(3\) 行有 \(n-1\) 个数（\(0\) 或 \(1\)），表示第一个地窖至第 \(2\) 个、第 \(3\) 个 \(\dots\) 第 \(n\) 个地窖有否路径连接。如第 \(3\) 行为 \(11000\cdots 0\)，则表示第 \(1\) 个地窖至第 \(2\) 个地窖有路径，至第 \(3\) 个地窖有路径，至第 \(4\) 个地窖、第 \(5\) 个 \(\dots\) 第 \(n\) 个地窖没有路径。

第 \(4\) 行有 \(n-2\) 个数，表示第二个地窖至第 \(3\) 个、第 \(4\) 个 \(\dots\) 第 \(n\) 个地窖有否路径连接。

……

第 \(n+1\) 行有 \(1\) 个数，表示第 \(n-1\) 个地窖至第 \(n\) 个地窖有否路径连接。（为 \(0\) 表示没有路径，为 \(1\) 表示有路径）。

输出格式

第一行表示挖得最多地雷时的挖地雷的顺序，各地窖序号间以一个空格分隔，不得有多余的空格。

第二行只有一个数，表示能挖到的最多地雷数。

样例 #1

样例输入 #1

5
10 8 4 7 6
1 1 1 0
0 0 0
1 1
1

样例输出 #1

1 3 4 5
27

提示

【题目来源】

NOIP 1996 提高组第三题

sol 1

因为数据很水，暴力搜索完全OK,这里讲正解。
很容易想到，如果当前一个节点的只是最优的，那么它的前驱也一定是最优的，不难得到状态转移方程
\(f_i=max{f_j} + a_i\)
其中\(j\)是\(i\)的前缀。

code-1

#include<bits/stdc++.h>
using namespace std;
const int N=25;
int f[N];
int a[N];
int n;
int g[N][N];
int pre[N];
int ansn;
int ansi;
void print(int x){
    if(pre[x]) print(pre[x]);
    cout<<x<<" ";
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i],f[i]=a[i];
    for(int i=1;i<n;i++)
        for(int j=i+1;j<=n;j++)
            cin>>g[i][j];
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(g[j][i]&&f[j]+a[i]>f[i]){//找最大的前驱
                f[i]=f[j]+a[i];
                pre[i]=j;
            }
            if(f[i]>ansn){
                ansn=f[i];
                ansi=i;
            }
        }
    }
    print(ansi);
    cout<<endl;
    cout<<ansn<<endl;
    return 0;
}            

T2

https://www.luogu.com.cn/problem/P1434

[SHOI2002] 滑雪

题目描述

Michael 喜欢滑雪。这并不奇怪，因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子：

1   2   3   4   5
16  17  18  19  6
15  24  25  20  7
14  23  22  21  8
13  12  11  10  9

一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度会减小。在上面的例子中，一条可行的滑坡为 \(24-17-16-1\)（从 \(24\) 开始，在 \(1\) 结束）。当然 \(25\)－\(24\)－\(23\)－\(\ldots\)－\(3\)－\(2\)－\(1\) 更长。事实上，这是最长的一条。

输入格式

输入的第一行为表示区域的二维数组的行数 \(R\) 和列数 \(C\)。下面是 \(R\) 行，每行有 \(C\) 个数，代表高度(两个数字之间用 \(1\) 个空格间隔)。

输出格式

输出区域中最长滑坡的长度。

样例 #1

样例输入 #1

5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9

样例输出 #1

25

提示

对于 \(100\%\) 的数据，\(1\leq R,C\leq 100\)。

sol 2

这道题其实是一个练习记忆化搜索的肥肠好的题目。
每搜索完一个高度的最长路径记录一下，以后搜索其他的点时如果走到了这条路就直接用记录的值计算就是了。

But,这是\(DP\)题单里的题目。
但说实在的，感觉DP和搜索差不多，\(f[i][j]\)只能从四个方向走过来,而且四个方向的点的高度要大于这个点,于是就可以了。
这里贴了个DP的。（自我感觉写的还是很清楚的）

code 2

#include<bits/stdc++.h>
using namespace std;
const int N=105;
int f[N][N];
int a[N][N];
int dx[4]={0,-1,0,1},dy[4]={-1,0,1,0};
int r,c;
int DFS(int x,int y){
    if(f[x][y]) return f[x][y];
    int t=1;
    for(int i=0;i<4;i++){
        int nx=x+dx[i];
        int ny=y+dy[i];
        if(nx>=1&&nx<=r)
            if(ny>=1&&ny<=c)
                if(a[nx][ny]<a[x][y]){
                    t=max(t,DFS(nx,ny)+1);
                }
    }
    f[x][y]=t;
    return t;
}
int main(){
    cin>>r>>c;
    for(int i=1;i<=r;i++)
        for(int j=1;j<=c;j++)
            cin>>a[i][j];
    int ans=-0x3f3f3f3f;        
    for(int i=1;i<=r;i++)
        for(int j=1;j<=c;j++){
            f[i][j]=DFS(i,j);
            ans=max(ans,f[i][j]);
        }
    cout<<ans<<endl;
    return 0;    
}

T3

https://www.luogu.com.cn/problem/P4017

最大食物链计数

题目背景

你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述

给你一个食物网，你要求出这个食物网中最大食物链的数量。

（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

Delia 非常急，所以你只有 \(1\) 秒的时间。

由于这个结果可能过大，你只需要输出总数模上 \(80112002\) 的结果。

输入格式

第一行，两个正整数 \(n、m\)，表示生物种类 \(n\) 和吃与被吃的关系数 \(m\)。

接下来 \(m\) 行，每行两个正整数，表示被吃的生物A和吃A的生物B。

输出格式

一行一个整数，为最大食物链数量模上 \(80112002\) 的结果。

样例 #1

样例输入 #1

5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4

样例输出 #1

5

提示

各测试点满足以下约定：

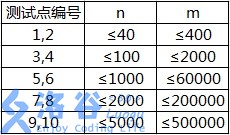
【补充说明】

数据中不会出现环，满足生物学的要求。（感谢 @AKEE ）

sol 3

着这么看都是个\(Topo\)(不知道为什么要放到\(DP\)题单里面来)。

那你们就直接\(Topo\)一下吧……
（不要说你不会拓扑排序，不会拓扑的就自行看题解吧，不知道我以后会不会更新到图论）

code 3

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=5005;
const int M=80112002;
vector<int>g[N];
int ind[N];
int cnt[N];
int oud[N];
int ans;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cin>>n>>m;
    while(m--)
    {
        int x,y;
        cin>>x>>y;
        g[x].push_back(y);
        ind[y]++;
        oud[x]++;
    }
    queue<int>q;
    for(int i=1;i<n;i++)
    {
        if(!ind[i]) q.push(i),cnt[i]=1;
    }
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int v:g[u])
        {
            ind[v]--;
            cnt[v]+=cnt[u];
            cnt[v]%=M;
            if(!ind[v])
            {
                q.push(v);
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(!oud[i]) ans+=cnt[i],ans%=M;
    }
    cout<<ans;
    return 0;
}

T4

https://www.luogu.com.cn/problem/P1115

最大子段和

题目描述

给出一个长度为 \(n\) 的序列 \(a\)，选出其中连续且非空的一段使得这段和最大。

输入格式

第一行是一个整数，表示序列的长度 \(n\)。

第二行有 \(n\) 个整数，第 \(i\) 个整数表示序列的第 \(i\) 个数字 \(a_i\)。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

7
2 -4 3 -1 2 -4 3

样例输出 #1

4

提示

样例 1 解释

选取 \([3, 5]\) 子段 \(\{3, -1, 2\}\)，其和为 \(4\)。

数据规模与约定

• 对于 \(40\%\) 的数据，保证 \(n \leq 2 \times 10^3\)。
• 对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 2 \times 10^5\)，\(-10^4 \leq a_i \leq 10^4\)。

sol 4

这是一道肥肠简单的题目了。虽然DP引入都挺简单的
定义\(f_i\)为以\(i\)点结尾的连续子串的最大和，从前往后遍历，对于某个点，如果以此结尾的连续子串的最大和，即\(f_i<0\),那么遍历到\(i+1\)时，更优的选择是将\(i+1\)之前的前缀舍去，把\(i+1\)作为新的子串的开头。而对于\(f_i>0\)的情况（\(f_i=0\)时两种处理方式都可以）将这组子串作为\(i+1\)的前缀。
重要代码：

if(f[i-1]<0) f[i]=a[i];
    else f[i]=f[i-1]+a[i];

Easy……

code 4

#include<bits/stdc++.h>
using namespace std;
int n;
const int N=2e5+5;
int a[N];
int f[N];
int ans=-0x3f3f3f3f;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    ans=f[1]=a[1];
    for(int i=2;i<=n;i++){
        if(f[i-1]<0) f[i]=a[i];
        else f[i]=f[i-1]+a[i];
        ans=max(ans,f[i]);
    }
    cout<<ans<<endl;
    return 0;
}

T5

https://www.luogu.com.cn/problem/P1802

5 倍经验日

题目背景

现在乐斗有活动了！每打一个人可以获得 5 倍经验！absi2011 却无奈的看着那一些比他等级高的好友，想着能否把他们干掉。干掉能拿不少经验的。

题目描述

现在 absi2011 拿出了 \(x\) 个迷你装药物（嗑药打人可耻…），准备开始与那些人打了。

由于迷你装药物每个只能用一次，所以 absi2011 要谨慎的使用这些药。悲剧的是，用药量没达到最少打败该人所需的属性药药量，则打这个人必输。例如他用 \(2\) 个药去打别人，别人却表明 \(3\) 个药才能打过，那么相当于你输了并且这两个属性药浪费了。

现在有 \(n\) 个好友，给定失败时可获得的经验、胜利时可获得的经验，打败他至少需要的药量。

要求求出最大经验 \(s\)，输出 \(5s\)。

输入格式

第一行两个数，\(n\) 和 \(x\)。

后面 \(n\) 行每行三个数，分别表示失败时获得的经验 \(\mathit{lose}_i\)，胜利时获得的经验 \(\mathit{win}_i\) 和打过要至少使用的药数量 \(\mathit{use}_i\)。

输出格式

一个整数，最多获得的经验的五倍。

样例 #1

样例输入 #1

6 8
21 52 1
21 70 5
21 48 2
14 38 3
14 36 1
14 36 2

样例输出 #1

1060

提示

【Hint】

五倍经验活动的时候，absi2011 总是吃体力药水而不是这种属性药。

【数据范围】

• 对于 \(10\%\) 的数据，保证 \(x=0\)。
• 对于 \(30\%\) 的数据，保证 \(0\le n\le 10\)，\(0\le x\le 20\)。
• 对于 \(60\%\) 的数据，保证 \(0\le n,x\le 100\)， \(10<lose_i,win_i\le 100\)，\(0\le use_i\le 5\)。
• 对于 \(100\%\) 的数据，保证 \(0\le n,x\le 10^3\)，\(0<lose_i\le win_i\le 10^6\)，\(0\le use_i\le 10^3\)。

【题目来源】

fight.pet.qq.com

absi2011 授权题目

sol 5

一个变形版的\(01背包\)。

\(f_i\)表示用\(i\)瓶药获得的最多经验。

And，决策？

当 \(i>=\) use时，可以选择打败或者不打败

\(f_i=max(f_i+lose,f_i-use+win)\)

当 \(i<use\) 时，无法战胜对方。

\(f_i+=lose\) //注意了，不嗑药也可以拿失败经验的哦

……不开\(longlong\)见祖宗哦……

code 5

#include<bits/stdc++.h>
using namespace std;
int n,x;
const int N=1e3+5;
int f[N];
int lose[N];
int win[N];
int ko[N];
int main(){
    cin>>n>>x;
    for(int i=1;i<=n;i++)  cin>>lose[i]>>win[i]>>ko[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=x;j>=ko[i];j--)
            f[j]=max(f[j]+lose[i],f[j-ko[i]]+win[i]);
        for(int j=ko[i]-1;j>=0;j--)
            f[j]+=lose[i];
    }
    cout<<(long long)5*f[x]<<endl;
    return 0;
}

这是 Day 2，讲累了，下次接着讲，争取在24年联赛之前讲完DP的大部分内容。(#^.#)