2024MX-MF-DAY1-text题解
T1
【题目描述】
有 \(n\) 个人按编号从 \(1\) 到 \(n\) 坐成一圈,即第 \(i \in [1,n]\) 个人右边是 \(i + 1\) ,第 \(n\) 个人右边的人是 \(1\)。
初始,每个人手上有 \(m\) 个球。随后,\(n\) 个人按编号从小到大的顺序依次执行如下操作:
- 把自己手中的球分成数量相同且尽可能多的三份,扔掉剩余的球,再把分得的三份分别给自己、左边的人,以及右边的人。
问所有人均操作完一次后,有球最多的人有几个球。
【输入格式】
从标准输入读入数据。
一行两个整数 \(n\),\(m\)。
【输出格式】
输出到标准输出。
一行表示一个整数表示答案。
【数据范围】
对于 \(50 \%\) 的数据: \(3 \le n,m \le 10\)
对于 \(70 \%\) 的数据: \(3 \le n,m \le 10^7\)
对于 \(100 \%\) 的数据: \(3 \le n,m \le 10^12\)
思路
赛时思路:
直接暴力模拟喜提 \(70pts\)
\(100pts\) 思路:
假设每个人手上的球颜色不同,那么显然每种颜色的球 最多延申(被传递) \(O(\log_3 m)\) 次(只能对(当前为 \(i\)) \(O(i-\log_3 m)\sim O(i+\log_3 m)\) 产生影响),故从 \(O(\log m)\) 个人开始,手上的球的变化就是重复的了,模拟前 \(O(\log m)\) 个人即可。
点击查看代码
#include <iostream>
using namespace std;
int main(){
int n, m;
cin >> n >> m;
int x = m / 3, val = 0;
for(int i = 2,last = m;i <= m;i++){
int now = last / 3 + m;
if(now == last || n == i){
val = now;
break;
}
last = now;
}
cout << x + (m + x) / 3 + (val + x) / 3 << '\n';
return 0;
}
T2
折线(line)
【题目描述】
图 1:
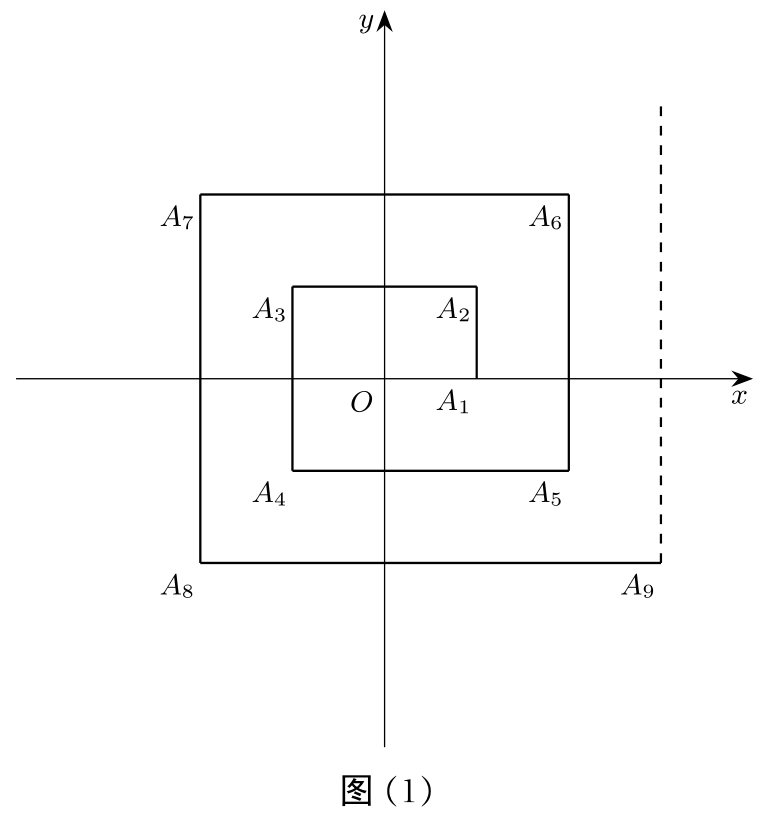
如上,在平面直角坐标系 \(\text{xOy}\) 中,有点 \(A_1(1, 0), A_2(1, 1), A_3(−1, 1), A_4(−1, −1), A_5(2, −1), \dots\),有 \(q\) 次询问形如:
1 n,询问点 \(A_n\) 的坐标;2 l r,询问折线段 \(A_lA_{l+1}A_{l+2} . . . A_{r−1}A_{r}\) 的长度;
【输入格式】
从标准输入读入数据。
第一行一个正整数 \(q\),表示询问总数。
接下来 \(q\) 行,每行一个询问形如 1 n 或 2 l r。
【输出格式】
输出到标准输出。
对于每一个询问,如果是 \(1\) 询问,输出一行两个整数表示 \(A_n\) 的 \(x\) 和 \(y\) 坐标,如果是 \(2\) 询问,输出一行一个整数表示折线长度。
【数据范围】
对于 \(100\%\) 的数据,\(1\le n\le 10^9,1\le l < r\le 10^6,1\le q\le 10^5\)。
思路
\(1\) 询问分类讨论,\(2\) 询问不难发现到显然线段长度是两个等差数列求和直接预处理即可。
点击查看代码
#include <iostream>
using namespace std;
long long x[1000000];
int main() {
int n;
cin >> n;
for (int i = 1; i < 1000000; i++) {
if (i % 2 == 1) {
x[i] = x[i - 1] + (i + 1) / 2;
} else {
x[i] = x[i - 1] + i / 2 + 1;
}
}
for (int i = 1; i <= n; i++) {
int a, b, c;
cin >> a;
if (a == 1) {
cin >> b;
if (b % 4 == 1) {
cout << b / 4 + 1 << " " << (b / 4 + 1) * (-1) + 1 << endl;
} else if (b % 4 == 2) {
cout << b / 4 + 1 << " " << b / 4 + 1 << endl;
} else if (b % 4 == 3) {
cout << (b / 4 + 1) * (-1) << " " << b / 4 + 1 << endl;
} else {
cout << (b / 4) * (-1) << " " << (b / 4) * (-1) << endl;
}
} else {
cin >> b >> c;
cout << x[c - 1] - x[b - 1] << endl;
}
}
return 0;
}
T3
STL
【题目描述】
有 \(n\) 个初始由空格隔开的字符串 \(s_1, s_2,\dots, s_n\),每一个均为 \(\texttt{int}\)、\(\texttt{vector}\) 或 \(\texttt{pair}\) 之一。
现在他希望在字符串之间以及最后一个字符串之后的空格中添上 \(<\)、\(>\)、\(,\)(可以不填),使得现在整个字符串可以代表一个 \(\text{C++14}\) 中的合法数据类型。
例如:
\(\texttt{int}\) 本身合法。
\(\texttt{vector int}\) 可以变成 vector
\(\texttt{pair int int}\) 可以变成 pair<int,int> 使之合法。
\(\texttt{pair vector pair int vector int pair vector int int}\) 可以变成
\(\texttt{pair<vector<pair<int,vector<int>>>,pair<vector<int>,int>>}\) 使之合法。
小 L 对此感到好奇,于是他给你 \(m\) 个操作,每个操作形如:
l r op:询问 \([l, r]\) 是否可以通过执行上述操作得到一个合法的数据类型。若 \(op = 1\) 且有解,你还要给出一种方案。若有多解,你可以输出任意一种。
【输入格式】
从标准输入读入数据。
本题包含多组数据。
第一行两个正整数 \(n, m\);
接下来一行 \(n\) 个用空格隔开的字符串 \(s_1, s_2,\dots, s_n\);
接下来 \(m\) 行,每行三个整数 \(l, r, op\)。
【输出格式】
输出到标准输出。
对每个询问,首先输出一行 Yes 或 No 表示解是否存在。若该询问对应的 \(op = 1\),你还需要再输出一行代表一组解,若有多解,你可以输出任意一种。
【数据范围】
对于 \(100\%\) 的数据,\(1\le n\),\(m\le 10^6\),\(s_i\) 为 \(\texttt{int vector pair}\) 中的一种,\(1\le l\le r\le n\),\(op \in\{0, 1\}\),\(op = 1\) 且有解时的 \(\sum(r − l + 1)\le 10^6\)。
思路
首先我们注意到这个 SPJ 是在诈骗。
注意到 \(\texttt{int}、\texttt{vector}、\texttt{pair}\) 的合法组合事实上是一个后缀表达式,其中 \(\texttt{int}\) 为操作数,\(\texttt{vector}\) 为一元操作符, \(\texttt{pair}\) 为二元操作符。于是合法时方案唯一。
那我们如何构造一个合法方案呢?
看到后缀表达式,我们考虑用一个栈来记录信息。栈中每个元素表示一个区间 \([L,R]\),表示区间 \([L,R]\) 是一个合法的后缀表达式。每次从右往左扫,遇到 \(\texttt{int}\) 直接将 \([i,i]\) 入栈;遇到 \(\texttt{vector}\) 将栈顶的弹出并放入 \([i,R]\),在 \(i,i+1\) 之间放入一个 <,再在 \(R,R+1\) 之间放入一个 >;遇到 \(\texttt{pair}\) 将栈顶的 \([i+1,R_1][R_1,R_2]\) 弹出并放入 \([i,R_2]\),在 \(i,i+1\) 之间放入一个 <,在 \([R_1,R_1+1]\) 之间放入一个 ,,最后在 \([R_2,R_2+1]\) 之间放入一个 > 即可。
以上任何一步需要弹栈时栈空或最终栈中元素个数不为 \(1\) 时无解。
那要是我们不需要构造方案呢?
现在依次考虑上述无解的两个条件。
最终栈中元素个数:注意到每遇到一个 \(\texttt{int}\),栈中元素个数 \(+1\) ;每遇到一个 \(\texttt{vector}\),栈中元素个数不变;每遇到一个 \(\texttt{pair}\),栈中元素个数 \(-1\)。
于是我们预处理一个每个位置对栈中元素个数贡献的前缀和 \(sum\),每次判断 \(sum_r-sum_{l-1}\) 是否为 \(1\) 即可。
弹栈时栈不空:对于所有 \(\texttt{vector}\) 出现的位置,我们需要后缀和 \(\ge 1\);对于所有 \(\texttt{pair}\) 出现的位置,我们需要后缀和 \(\ge 2\)。
当然,我们可以运用 ST 表等 RMQ 算法求出区间后缀和最小值,但是超纲了。
对于 \(\texttt{vector}\) 的条件,我们需要知道 \([l-1,r-1]\) 中的 \(sum_i\) 中是否有 \(\ge sum_r\) 者——即 \(<r\) 的第一个
满足 $ >sum_r$ 的位置是否不存在或 \(<l-1\);对于 \(\texttt{pair}\) 的条件,我们需要知道 \([l-1,r-1]\) 中的 \(sum_i\)
中是否有 $ >sum_r$ 者——即 \(<r\) 的第一个满足 $ >sum_r$ 的位置是否不存在或 \(<l-1\)。
分别排序后离线链表即可。时间复杂度为 \(O(n \log n + m)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,c[1000005],pre[1000005],Log[1000005],st[22][1000005],l,r,op;char s[15];
struct Link
{
int pre,nxt;char c;
}a[10000005];
int query(int l,int r)
{
if(l>r)return 0x3f3f3f3f;
int k=Log[r-l+1];
return min(st[k][l],st[k][r-(1<<k)+1]);
}
int main()
{
cin.tie(0)->sync_with_stdio(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>s;
if(s[0]=='i')c[i]=1;
else if(s[0]=='v')c[i]=2;
else c[i]=3;
}
for(int i=1;i<=n;i++)pre[i]=pre[i-1]+(c[i]==1?-1:(c[i]==2?0:1));
for(int i=1;i<=n;i++)st[0][i]=pre[i];
for(int i=1;(1<<i)<=n;i++)
{
for(int j=1;j+(1<<i)-1<=n;j++)st[i][j]=min(st[i-1][j],st[i-1][j+(1<<(i-1))]);
}
for(int i=2;i<=n;i++)Log[i]=Log[i>>1]+1;
while(m--)
{
cin>>l>>r>>op;
if(pre[r]-pre[l-1]!=-1||query(l,r-1)-pre[l-1]<=-1)cout<<"No\n";
else
{
cout<<"Yes\n";
if(op==1)
{
stack<pair<int,int> >st;
int tot=0;
for(int i=r;i>=l;i--)
{
if(c[i]==1)
{
a[++tot].c='i';a[++tot].c='n';a[++tot].c='t';
for(int j=0;j<3;j++)a[tot-j].pre=tot-j-1,a[tot-j].nxt=tot-j+1;
if(st.size())a[tot].nxt=st.top().first;
else a[tot].nxt=0;
a[tot-2].pre=0;
st.push(make_pair(tot-2,tot));
}
else if(c[i]==2)
{
int l=st.top().first,r=st.top().second;st.pop();
a[++tot].c='v';a[++tot].c='e';a[++tot].c='c';
a[++tot].c='t';a[++tot].c='o';a[++tot].c='r';a[++tot].c='<';
for(int j=0;j<7;j++)a[tot-j].pre=tot-j-1,a[tot-j].nxt=tot-j+1;
a[tot-6].pre=0;a[tot].nxt=l;a[l].pre=tot;
a[++tot].c='>';
a[tot].pre=r;a[tot].nxt=a[r].nxt;a[r].nxt=tot;
st.push(make_pair(tot-7,tot));
}
else
{
int pl=st.top().first,pr=st.top().second;st.pop();
int ql=st.top().first,qr=st.top().second;st.pop();
a[++tot].c='p';a[++tot].c='a';a[++tot].c='i';a[++tot].c='r';a[++tot].c='<';
for(int j=0;j<5;j++)a[tot-j].pre=tot-j-1,a[tot-j].nxt=tot-j+1;
a[tot-4].pre=0;a[tot].nxt=pl;a[pl].pre=tot;
a[++tot].c=',';
a[tot].pre=pr;a[tot].nxt=ql;a[pr].nxt=tot;a[ql].pre=tot;
a[++tot].c='>';
a[tot].pre=qr;a[tot].nxt=a[qr].nxt;a[qr].nxt=tot;
st.push(make_pair(tot-6,tot));
}
}
for(int i=st.top().first;i;i=a[i].nxt)cout<<a[i].c;
for(int i=1;i<=tot;i++)a[i].pre=a[i].nxt=a[i].c=0;
cout<<'\n';
}
}
}
return 0;
}
T4
【题目描述】
现在有 \(n\) 个白色的球串成了一个圆环,编号依次为 \(1,2,3,\dots,n\),现在你需要把这些球都染黑,具体操作为:
1.等概率随机地选择一个之前从未选过的球(白球、黑球都可以)。
2.将该球和它相邻的两个球都染黑。
3.如果所有白球都染黑,那么结束。
求出染黑所有白球的期望步数,答案对 \(998244353\) 取模。
【输入格式】
一行一个正整数 \(n\),表示白球的个数。
【输出格式】
一行一个数字,表示期望步数,对 \(998244353\) 取模。
【数据范围与提示】
对于 \(100\%\) 的数据,\(3 < n < 5000\)。
思路
\(100pts\) 需要高中乃至大学知识,我只会 \(40pts\) 的暴力搜索。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int mod = 998244353;
int Pow(int a, int b) {
int res = 1;
while (b) {
if (b & 1)
res = 1LL * res * a % mod;
a = 1LL * a * a % mod;
b >>= 1;
}
return res;
}
int a[15], f[15];
int n;
int sum = 0;
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) f[i] = i;
do {
for (int i = 1; i <= n; i++) a[i] = 0;
int cnt = 0;
for (int i = 1; i <= n; i++) {
int now = f[i];
int pre = ((now == 1) ? n : (now - 1));
int nxt = ((now == n) ? 1 : (now + 1));
cnt += (!a[pre]);
a[pre] = 1;
cnt += (!a[now]);
a[now] = 1;
cnt += (!a[nxt]);
a[nxt] = 1;
if (cnt == n) {
sum = (sum + i) % mod;
break;
}
}
} while (next_permutation(f + 1, f + n + 1));
int s = 1;
for (int i = 1; i <= n; i++) s = 1LL * s * i % mod;
cout << 1LL * sum * Pow(s, mod - 2) % mod;
return 0;
}