三（四）元环

Benzenesir / 2023-09-03 / 原文

模拟赛考了这个东西，被创死了

其实总结下来就一个东西，如果我们给边定向，让度数小的向度数大的连，那所有点的出度不会超过$\sqrt{m}$

根号分治，如果本身的度数小于$\sqrt{m}$，则明显合法，若大于了，则最多只有$\sqrt{m}$ 个点的度数大于了当前点

一个三元环可以被拆成 $A\rightarrow B$，$A \rightarrow C$,$ B \rightarrow C$，那不妨枚举一个点周围所有的点，然后再枚举周围的点周围的点，如果被染色了，就可知有三元环存在

四元环就大同小异了，一个四元环定向之后的形态就两种

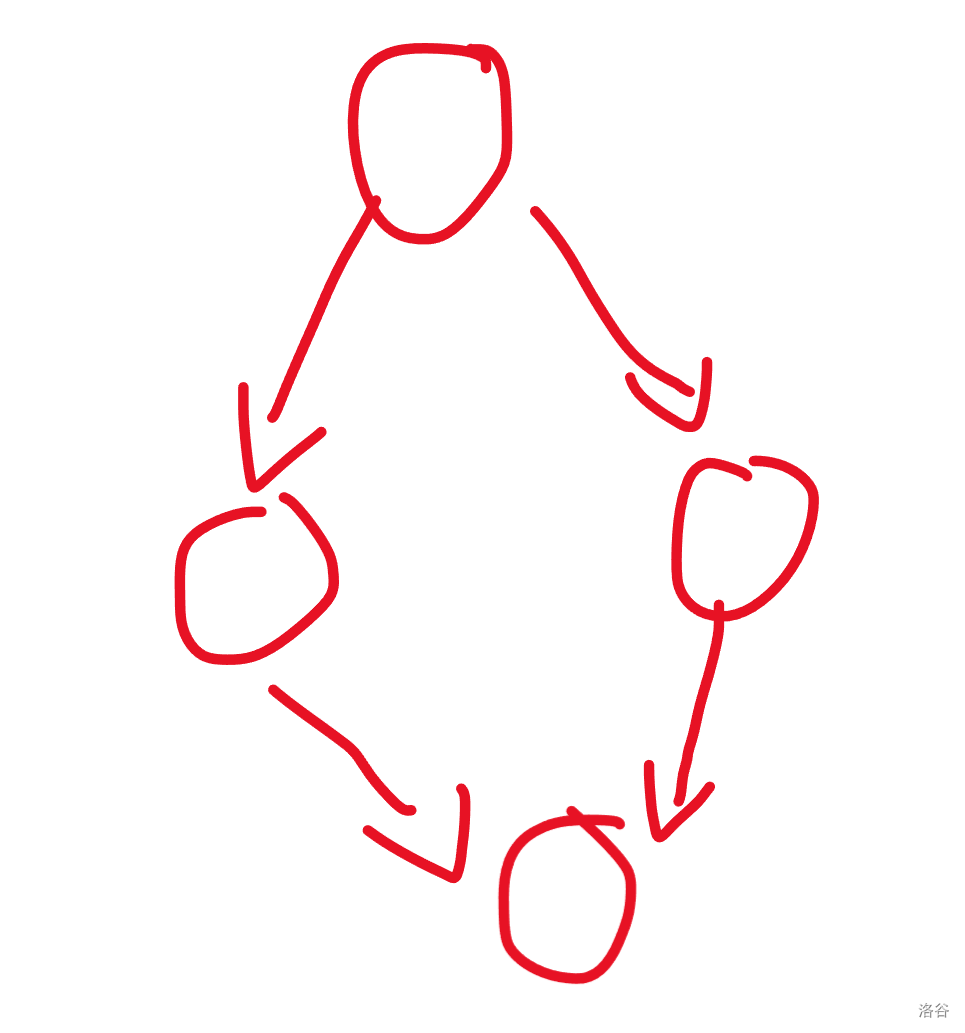
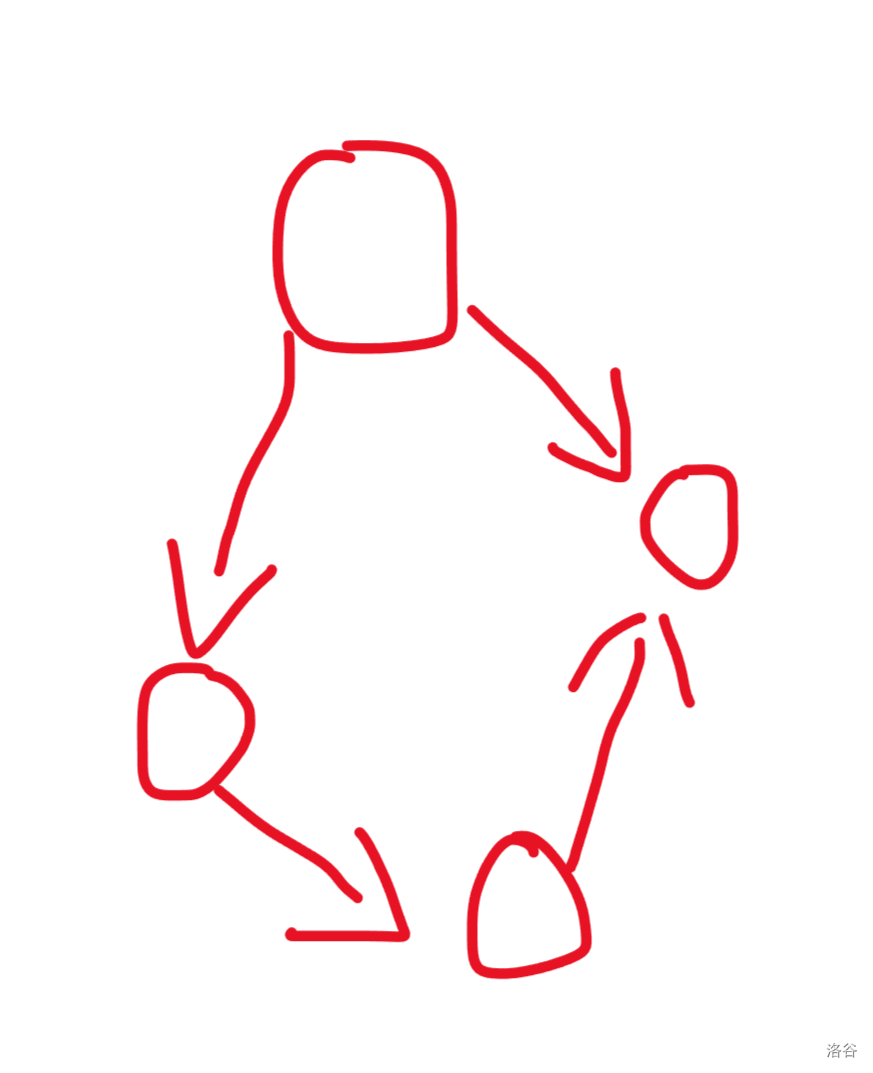
我们考虑在入度最多的点处统计答案，固定其对面的点，枚举其在原图上的边，再在这个点上枚举其定向边，加进答案统计就可以了

但这样会统计出事，因为对于第一张图，你从两边的点开始，也能统计出整个环，所以要求当起点的度数小于终点的度数时才能统计

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	n=rd(),k=rd(),m=rd();
	fp(i,1,m){
		int x=rd(),y=rd()+n;
		g[x].emplace_back(y),
		g[y].emplace_back(x);
		deg[x]++,deg[y]++;
	}
	iota(id+1,id+n+k+1,1);
	sort(id+1,id+n+k+1,[](int x,int y){
		return deg[x]<deg[y];
	});
	n+=k; 
	fp(i,1,n) rk[id[i]]=i;
	fp(i,1,n)
		for(int x:g[i])
			if(rk[x]>=rk[i])
				ng[i].emplace_back(x);
	ll ans=0;
	fp(i,1,n){
		for(int x:g[i])
			for(int y:ng[x])
				if(rk[i]<rk[y])
					ans+=ts[y]++;
		for(int x:g[i])
			for(int y:ng[x])
				ts[y]=0;
	}
	cout << ans << endl;
	return 0;
}

代码不是标准模板，仅供参考，慎重查看