C. The Football Season 数学exgcd

题意:
给你四个数,n,p,d,w。让你求出任意一组x,y,z,要满足下面的条件
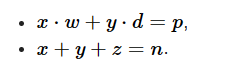
做法:
对于第一个式子,我们可以先用exgcd求出合法的解,在他的整个解系中进行mod(k)+k再mod(k)的操作,判断x和y能否同时非负。
对于第二个式子,我们要让z非负,那么x+y要尽可能小。而还要满足第一个式子,我们就得贪心一下,那就是让y尽可能小,所以上面说的第一步就是对y来进行的。然后判断x是否大于零以及x+y是否小于等于n就好了。值得一提的是这题要开int128。就是在exgcd完事之后再求y的时候要开。有时候过了不是不用开,只是出题人没卡。
#include<bits/stdc++.h>
#define de cout<<111<<"\n";
#define fi first
#define se second
#define ll long long
#define kx(a,b) ((a*b)%mod)
#define kplus(a,b) ((a+b)%mod)
#define lowbit(x) x&(-x);
#define up(a,b) ((a-1ll)/b+1ll)
typedef __int128 Int;
using namespace std;
const int N=1000010;
const ll mod=998244353;
//const int mod=1000000007;
typedef pair<int,int> pii;
ll fect[N], infect[N];
ll binpow(ll a,ll b,ll c){
ll ans=1;
while(b){
if(b&1)
ans=(Int)ans*a%c;
a=(Int)a*a%c;
b>>=1;
}
return ans;}
int C(int a,int b){
return fect[a]*infect[b]%mod*infect[a-b]%mod;}
void initzuhe(int n){
fect[0]=1;infect[0]=1;
for(int i=1;i<=n;i++){
fect[i]=(fect[i-1]*i)%mod;
}
infect[n-1]=binpow(fect[n-1],mod-2ll,mod);
for(int i=n-2;i>=1;i--)
infect[i]=infect[i+1]*(i+1ll)%mod;}
ll test[12]={2,3,5,7,11,13,17,19,23,29,31,37},maxn;
bool check(ll a,ll n){
ll d=n-1,get=binpow(a,d,n);
if(get!=1) return 1;
while((d&1)^1)
if(d>>=1,(get=binpow(a,d,n))==n-1) return 0;
else if(get!=1) return 1;
return 0;}
bool miller_rabbin(ll n)
{
if(n<40){
for(int i=0;i<12;i++) if(test[i]==n) return 1;
return 0;
}
for(int i=0;i<12;i++) if(check(test[i],n)) return 0;
return 1;}
ll gcd(ll a,ll b){
return !b?a:gcd(b,a%b);}
inline ll f(ll x,ll c,ll n){
return ((Int)x*x+c)%n;}
ll pollard_rho(ll x){
ll s=0,t=0,c=1ll*rand()%(x-1)+1,val=1;
for(int i=1;;i<<=1,s=t,val=1){
for(int j=1;j<=i;j++){
t=f(t,c,x);
val=(Int)val*abs(t-s)%x;
if(!(j%127)){
ll d=gcd(val,x);
if(d>1) return d;
}
}
ll d=gcd(val,x);
if(d>1) return d;
}}
ll x,y;
ll exgcd(ll a,ll b,ll &x,ll &y){
if(b==0){
x=1ll,y=0ll;
return a;
}
ll temp=exgcd(b,a%b,x,y);
ll z=x;x=y;
y=z-a/b*y;
return temp;
}
void solve(){
ll n,p,w,d;cin>>n>>p>>w>>d;
ll g=gcd(w,d);
if(p%g!=0){
cout<<-1<<"\n";return ;
}
exgcd(w,d,x,y);
ll k=w/g;
Int yy=(Int)y*((Int)p/(Int)g);
yy=(yy%k+k)%k;
x=(p-d*yy)/w;
y=yy;
if(x<0){
cout<<-1<<"\n";return ;
}
ll z=n-x-y;
if(z>=0)cout<<x<<" "<<y<<" "<<z<<"\n";
else cout<<-1<<"\n";
}
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
srand((unsigned)time(NULL));
// int t;cin>>t;while(t--)
solve();
}