双指针算法及模板

1.第一类双指针算法

    第一类双指针算法指的就是：
        有两个序列A和B，同时有两个指针i和j。使得i指向其中一个序列，j指向另外一个序列。典型的应用就是在归并排序当中，将两个序列按照某一个规则进行排序时（从小到大或从大到小），使用的就是双指针算法。

2. 第二类双指针算法

    第二类双指针算法指的就是：
        有一个序列A，同时有两个指针i和j。使得i和j同时指向一个序列。典型的应用就是在快速排序中，当调整区间时，就是采用双指针算法来进行的。

3. 双指针算法的应用

    双指针算法的应用是非常之广泛的。具体采用哪一类双指针算法要根据题目具体问题具体分析。

4. 双指针算法的作用

    双指针算法的核心作用就在于可以优化暴力算法。如果某种问题通过暴力做法达到了O(n)以上的时间复杂度的话，且这道题可以采用双指针算法求解的话，那么采用双指针算法可以将问题优化到O(n)的时间复杂度。一般而言，双指针算法都是O(n)的时间复杂度。

5. 双指针算法模板

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}
常见问题分类：
    (1) 对于一个序列，用两个指针维护一段区间
    (2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

    关于双指针算法的模板，仅当做参考意义。因为双指针算法的应用十分广泛，模板不能代表所有情况，还是要具体问题具体分析。

6. 双指针算法例题

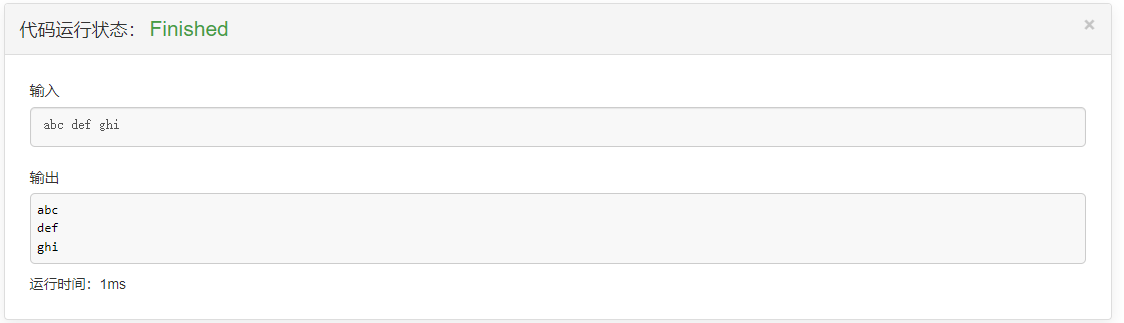
    第一个问题，假设有一个字符串，里面有很多单词，每个单词之间用空格隔开。接下来，请你用双指针算法来将每一个单词输出。

    这个问题是双指针算法最经典的应用。具体步骤如下：
        1. 首先，维护一个指针i，i指针每次都要确保指向每一个单词的起始位置。
        2. 其次，维护一个指针j，j刚开始也要指向起始位置，经过移动之后，j指针每次都要确保指向每一个单词的最后一个位置的下一个位置（空格）。
        3. i和j-1之间就是单词。
        4. 输出完单词之后，让i指向j+1，j指向i即可。之后重复以上操作即可。

#include <iostream>
#include <cstdio>
#include <string.h>
#include <string>

using namespace std;

int main(){
    char str[101];
    fgets(str,101,stdin);           //读入一整行
    int i,j;
    int length = strlen(str);
    for(int i=0;i<length;i++){
        //设定起始位置
        j = i;
        //移动j
        while(j < length && str[j] != ' '){
            j++;
        }
        //输出单词
        for(int k=i;k<j;k++){
            printf("%c",str[k]);
        }
        printf("\n");
        //输出单词之后调整i
        i = j;
    }
    return 0;
}

https://www.acwing.com/problem/content/801/

    这道题总体上难度较高，接下来采用双指针算法依次进行讲解。
    首先，我们需要了解双指针i和j的含义。i代表当前区间的右边界。j代表该区间满足连续不重复这个特点的最远的左边界。那么，i和j构成的区间是局部的最长连续不重复子序列。（不是全局，因为i不同）
    上述内容可能会不太容易理解，接下来我们会讲述实际的例子来辅助理解。
    例：1 2 2 3 5
    1.  初始，i和j都指向1，发现i和j所构成的区间没有重复的数，因此从局部上看构成了最长连续不重复子序列。（代表以i=1为终点（下标为0）的最长连续不重复子序列）长度为1。记录答案为1。
    2.  让i往后移动一个位置，此时i和j所构成的区间就是[1,2]，我们也可以发现i和j所构成的区间没有重复的数，因此从局部上看也构成了最长连续不重复子序列，（代表以i=2为终点（下标为1）的最长连续不重复子序列）长度为2。但是，题目要求找到全局的最长连续不重复子序列。因此，我们要从局部当中进行比较，找到长度最大的，就是本题的答案。从第一步中，我们找到了一个局部的序列，长度为1。目前，我们找到了长度为2的局部的序列。因此，记录答案为2。
    3.  让i往后移动一个位置，此时i和j所构成的区间为[1,2,2],我们可以发现该区间存在重复的数，不满足题目的条件。因此，让j往后移动一个位置。
    4.  此时i和j所构成的区间[2,2],我们同样可以发现该区间存在重复的数，不满足题目的条件。因此，继续让j往后移动一个位置。
    5.  此时i和j所构成的区间[2],我们发现i和j所构成的区间没有重复的数，因此从局部上看构成了最长连续不重复子序列，（代表以i=2为终点（下标为2）的最长连续不重复子序列）长度为1。但是，目前从全局来看，最长的长度为2，因此记录答案仍是为2。
    6.  让i往后移动一个位置，此时i和j所构成的区间为[2,3],我们发现i和j所构成的区间不存在重复的数，因此从局部上看构成了最长连续不重复子序列，（代表以i=3为终点（下标为3）的最长连续不重复子序列）长度为2。记录答案为2。
    7.  让i继续往后移动一个位置，此时i和j所构成的区间为[2,3,5],我们发现i和j所构成的区间不存在重复的数，因此从局部上看构成了最长连续不重复子序列（代表以i=5为终点（下标为4）的最长连续不重复子序列），长度为3。记录答案为3。因此，本案例中的最长连续不重复子序列为[2,3,5]
长度为3。
    那么，根据上述的步骤，我们可以发现如下规律和问题：
        1. i,j指针始终向后移动。当i往后移动的时候，j为何只能向后移动，而不是向前移动？
        2. 如何判断i和j所构成的区间没有重复的数？
        3. 当i每次往后移动的时候，i和j所构成的区间就会增加一个数。当j每次往后移动的时候，i和j所构成的区间就会减少一个数。
        4. 如果i和j所构成的区间没有重复的数，当i往后移动一个位置时，如果该区间存在了重复的数，那么重复的数就是i所指向的数。
    接下来，对上述的问题进行讲解。

    1. 为什么，j只能向后移动？
        解答：我们可以证明，当i往后移动的时候，j只能向后移动，证明过程如下：
            假设，i和j构成了一个局部的最长连续不重复子序列。(i是一定大于等于j的),j始终代表满足连续不重复这个性质的最远的位置。（即：最长连续不重复性质）
            那么，当i往后移动的时候，假设当前i和j所构成的区间存在了重复的数。此时让j往前移动一个位置，发现i和j所构成的区间中的数增多了。此时，i和j所构成的区间就不满足连续不重复这个性质了。因此，j只能往后移动。
    2. 怎么判断i和j所构成的区间没有重复的数？
        我们可以用一个数组S，来动态存储每一个数所出现的次数。从上述的规律中我们可以发现，当i和j所构成的区间出现了重复的数时，重复的点就是i指向的数。因此，我们只需要判断当i指向的数所出现的次数大于1时，就代表发生了重复，否则就没有发生重复。当i每次往后移动的时候，i所指向的数所出现的次数都要+1。(代表区间增加了一个数)当j每次往后移动的时候，都要让j之前所指向的数所出现的次数-1。(代表区间减少了一个数)

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

int q[100010];
int s[100010];                          //代表动态计数的数组
    
int main(){
    int n;
    int res = 0;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&q[i]);
    }
    int i,j;
    for(i=0,j=0;i<n;i++){
        s[q[i]]++;                       //代表区间要增加一个数
        while(s[q[i]] > 1){              //代表目前区间有重复元素
            s[q[j]]--;                   //代表区间要移除一个数
            j++;                         //j向后移动
        }
        res = max(res,i-j+1);            //计算长度（全局）
    }
    printf("%d",res);
    return 0;
}

https://www.acwing.com/problem/content/description/802/

    二分法求解思路：
        1.  先遍历i，遍历i的过程中，利用二分法来求解。当i下标确定后，a[i]就是其中一个加数。由于b数列是一个递增数列，所以我们可以采用二分法进行求解。

    2.  如何进行二分呢？
        1. 假设a[i]已经确定，由于题目给定的条件就是a[i] + b[j] == x。因此，我们可以根据这个条件将b数组划分为两个区间。使得，左区间为：a[i] + b[mid] < x 而右区间为:a[i] + b[mid] >= x。其中，mid = (l+r) >> 1;
        2. 当mid位于左区间的时候，mid是取不到答案的，因此更新方式为：l = mid + 1;
        3. 当mid位于右区间的时候，mid可能会取到答案，因此更新方式为：r = mid;
        4. 如此反复，直到l == r 为止。此时，b[l]就是二分法所找到的答案，但未必是这个题目的答案。
        5. 因此，我们需要判断二分法所找到的答案b[l] + a[i] 是否等于x，如果等于就是本道题的答案，如果不等于那么就继续遍历i，继续二分，直到找到本题答案为止。(这道题保证了一定有解且唯一)

#include <iostream>
#include <cstdio>
using namespace std;

int main(){
    int n,m,x;
    int a[100010];
    int b[100010];
    scanf("%d %d %d",&n,&m,&x);
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    for(int j=0;j<m;j++){
        scanf("%d",&b[j]);
    }
    for(int i=0;i<n;i++){
        int l = 0;
        int r = m;
        while(l < r){
            int mid = (l+r) >> 1;
            if(a[i] + b[mid] >= x){
                r = mid;
            }else{
                l = mid + 1;
            }
        }
        if(a[i] + b[l] != x){
            continue;
        }else{
            printf("%d %d",i,l);
        }
    }
    return 0;
}

    双指针法求解思路：
        1.  我们先让i指向第一个数组的第一个元素，让j指向第二个数组的最后一个元素。
        2.  对于每一个i，我们要寻找到a[i] + b[j] >= x的最小的j。
        3.  随着i增大，j一定是缩小的。因为i，j指向的数组都是升序的，i增大，i指向的数也增大，由于x是固定不变的，因此j一定会随着缩小。（换句话说：j只能往前移动）。
        4.  因此，根据上述的性质，我们可以构造出如下的判断条件：
            for(i=0,j=m-1;i<n;i++)
                while(j>=0 && a[i] + b[j] > x){
                    j--;
                }
                if(a[i] + b[j] == x){
                    输出下标
                    break;
                }

#include <iostream>
#include <cstdio>

using namespace std;

int A[100010];
int B[100010];

int main(){
    int n,m,x;
    scanf("%d %d %d",&n,&m,&x);
    for(int i=0;i<n;i++){
        scanf("%d",&A[i]);
    }
    for(int j=0;j<m;j++){
        scanf("%d",&B[j]);
    }
    for(int i=0,j=m-1;i<n;i++){
        while(j >= 0 && A[i] + B[j] > x){
            j--;
        }
        if(A[i] + B[j] == x){
            printf("%d %d\n",i,j);
            break;
        }
    }
    return 0;
}

https://www.acwing.com/problem/content/2818/

#include <iostream>
#include <cstdio>

using namespace std;

int a[100010];
int b[100010];

int main(){
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    for(int j=0;j<m;j++){
        scanf("%d",&b[j]);
    }
    int i = 0,j = 0;
    while(j<m && i<n){
        if(a[i] == b[j]){
            i++;
            j++;
        }else{
            j++;
        }
    }
    if(i == n){
        printf("Yes");
    }else{
        printf("No");
    }
    return 0;
}

    作者：gao79138
    链接：https://www.acwing.com/
    来源：本博客中的截图、代码模板及题目地址均来自于Acwing。其余内容均为作者原创。
    著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。